【构造共轭函数+矩阵快速幂】HDU 4565 So Easy! （2013 长沙赛区邀请赛）

本文主要是介绍【构造共轭函数+矩阵快速幂】HDU 4565 So Easy! （2013 长沙赛区邀请赛），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【题目链接】 ：click here~~

【题目大意】：

　A sequence S_n is defined as:

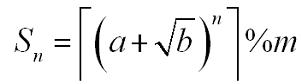
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S_n.
　　You, a top coder, say: So easy! 

【解题思路】

给一张神图，推理写的灰常明白了，关键是构造共轭函数，这一点实在是要有数学知识的理论基础，推出了递推式，接下来就是矩阵的快速幂了。

给个大神的链接：构造类斐波那契数列的矩阵快速幂

神图：click here~~

代码：

/*
* Problem: HDU No.4565
* Running time: 62MS
* Complier: G++
* Author: javaherongwei
* Create Time: 9:55 2015/9/21 星期一
*/#include <bits/stdc++.h>
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>using namespace std;
typedef long long LL;
const LL siz=2;          // max size of the matrix,
#define MODD(a,b) (((a%b)+b)%b)LL A,B,N,M,ret;
struct mut
{LL mat[siz][siz];mut(){memset(mat,0,sizeof(mat));}void init(LL a,LL b,LL c,LL d){mat[0][0]=a;mat[0][1]=b;mat[1][0]=c;mat[1][1]=d;}mut operator *(const mut &c){mut res;for(int i=0; i<siz; ++i){for(int k=0; k<siz; ++k){for(int j=0; j<siz; ++j){res.mat[i][j]=MODD(res.mat[i][j]+mat[i][k]*c.mat[k][j],M);}}}return res;}
}AC;mut poww(LL n)
{mut ans;ans.init(1,0,0,1);while(n){if(n&1) ans=ans*AC;n>>=1;AC=AC*AC;}return ans;
}int main()
{while(~scanf("%lld %lld %lld %lld",&A,&B,&N,&M)){if(N<=1){printf("%lld\n",2*A%M);}else{AC.init(2*A,B-A*A,1,0);mut ans=poww(N-1);printf("%lld\n",MODD(2*A%M*ans.mat[0][0]+2*ans.mat[0][1],M));}} return 0;
}

这篇关于【构造共轭函数+矩阵快速幂】HDU 4565 So Easy! （2013 长沙赛区邀请赛）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---