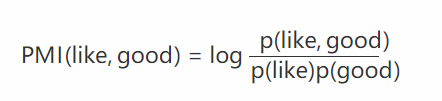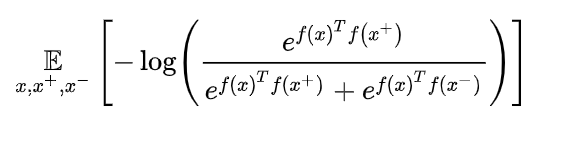互信息专题

第十四篇——互信息：相关不是因果，那相关是什么？

目录一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么？四、总结五、升华![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/499cd9af2ea14cbf8d12813f6f7fa150.png) 一、背景介绍通过本文，可以了解到信息之

MI-SegNet: 基于互信息的超越领域泛化的超声图像分割

文章目录 MI-SegNet: Mutual Information-Based US Segmentation for Unseen Domain Generalization摘要方法实验结果 MI-SegNet: Mutual Information-Based US Segmentation for Unseen Domain Generalization 摘要针对医

$条件熵，信息增益（互信息）与特征选择$

条件熵，信息增益（互信息）与特征选择

一定要先搞清楚什么是信息量，什么是信息熵。参考博文：https://blog.csdn.net/u010916338/article/details/91127242 一，什么是信息量？简言之，就是把信源看做是一个随机变量。消息（信号）就是随机变量的取值，比如a1，a2···an。信息就是这些随机变量的不确程度（发生概率越低，不确定性越大），公式如下。为什么写成这样呢？原因有二。第一：概率和

熵、信息熵、交叉熵、相对熵、条件熵、互信息、条件熵的贝叶斯规则

熵每条消息都含有信息。“信息熵”是“熵”的别名，用来衡量消息的不确定程度。宽泛来讲，即消息所传达的信息的模糊程度，消息越模糊，其熵越高。形象的说，熵是从根据模糊消息—>得到精确信息所需要花费的最小代价。熵=信息量(的期望)=不确定性的多少。熵值是信息量的一个度量。某种意义上说，熵就是最优策略。《数学之美》中这样描述：变量的不确定性越高，熵也就越大，要把它搞清楚，所

利用互信息比较不同的聚类结果

互信息（mutual information）和信息熵（information entropy）一样都是信息论里面的概念。信息熵在决策树里面用的比较多，可以度量样本集合的纯度。而互信息在聚类中有很大的作用，它可以衡量对同一个数据集不同的划分的之间的相似程度。假设 Pa，Pb P^a，P^b表示数据集 X X上的两个不同的划分，XX包括n的样本。 Pa P^a包含 ka k_a个簇， Pa

告别互信息:跨模态人员重新识别的变分蒸馏

Farewell to Mutual Information: Variational Distillation for Cross-Modal Person Re-Identification 摘要：信息瓶颈 (IB) 通过在最小化冗余的同时保留与预测标签相关的所有信息，为表示学习提供了信息论原理。尽管 IB 原理已应用于广泛的应用，但它的优化仍然是一个具有挑战性的问题，严重依赖于互信息的

Minepy—使用python计算最大互信息系数(MIC)

MIC 即：Maximal Information Coefficient 最大互信息系数。 https://blog.csdn.net/qtlyx/article/details/50780400 MIC可以用来衡量线性或非线性的相互关系。算法对比 https://zhuanlan.zhihu.com/p/53092905 MIC算法可以通过python的minpy包来实

安装minepy-用最大互信息系数法进行特征工程

利用minepy可以方便的利用最大互信息系数法进行特征工程，我在安装时遇到了以下问题，如图所示：错误原因因该是我的visual studio安装出了问题，我打开相应位置，发现我没有platformSDK文件夹我不想重装VS了，到网上寻找解决办法，发现可以从https://www.lfd.uci.edu/~gohlke/pythonlibs/网站上下载，如下图所示：下载后，切换到目录，用

100天精通风控建模(原理+Python实现)——第15天：风控建模中的互信息是什么？怎么实现？

风控模型已在各大银行和公司都实际运用于业务，用于营销和风险控制等。本文以视频的形式阐述风控建模中卡方检验是什么，怎么实现。并提供风控建模原理和Python实现文章清单。之前已经阐述了100天精通风控建模(原理+Python实现)——第1天：什么是风控建模？ 100天精通风控建模(原理+Python实现)——第2天：风控建模有什么目的？ 100天精通风控建模(原理+Python实

变分互信息蒸馏（Variational mutual information KD）

原文标题是Variational Information Distillation for Knowledge Transfer，是CVPR2019的录用paper。 VID方法思路比较简单，就是利用互信息（mutual information，MI）的角度，增加teacher网络与student网络中间层特征的MI，motivation是因为MI可以表示两个变量的依赖程度，MI越大，表明

条件互信息的理解(Conditional Mutual Information)

在概率论，尤其是信息论中，条件互信息的基本形式是在给定第三个变量值的情况下，两个随机变量互信息的期望值。对于离散随机变量X,Y,Z，其条件互信息为：用图形表示条件互信息为：具体的定义等后续补充。

互信息的简单理解

在介绍互信息之前，首先需要了解一下信息熵的概念：所谓信息熵，是指信息论中对一个随机变量不确定性的度量，对于随机变量x，信息熵的定义为： H ( x ) = − ∑ x p ( x ) l o g p ( x ) H(x)=-\sum_xp(x)logp(x) H(x)=−x∑p(x)logp(x) 随机变量的熵越大，说明这个变量带给我们的信息越多。互信息（MI，Mutual Info

拿捏！相关性分析，一键出图！皮尔逊、斯皮尔曼、肯德尔、最大互信息系数（MIC）、滞后相关性分析，直接运行！独家可视化程序！

适用平台：Matlab2020及以上相关性分析是一种统计方法，用于衡量两个或多个变量之间的关系程度。通过相关性分析，我们可以了解变量之间的相互关系、依赖性，以及它们是如何随着彼此的变化而变化的。相关性分析通常包括计算相关系数或其他衡量关联度的指标。 ①量化特征之间的关联程度：通过相关系数的值，我们可以判断它们的关系是强烈的、中等还是弱。 ②特征降维：在大规模数据集中，相关性分析可以帮助我们

互信息法的原理详解

文章目录互信息法（上）互信息是什么从信息增益角度理解互信息从变量分布一致角度理解互信息卡方检验与离散变量的互信息法互信息法（上）尽管f_regression巧妙的构建了一个F统计量，并借此成功的借助假设检验来判断变量之间是否存在线性相关关系，但f_regression仍然存在较大局限，首当其冲当然是f_regression只能挖掘线性相关关系，也就是两个变量的同步变化关

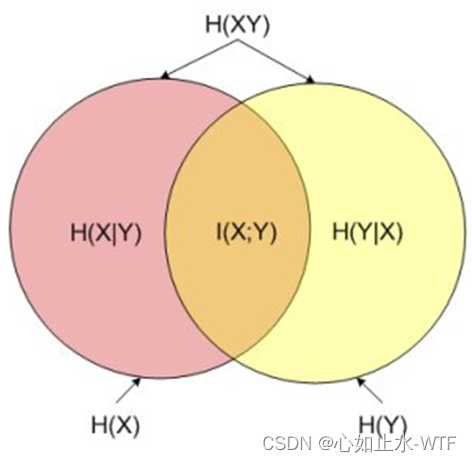
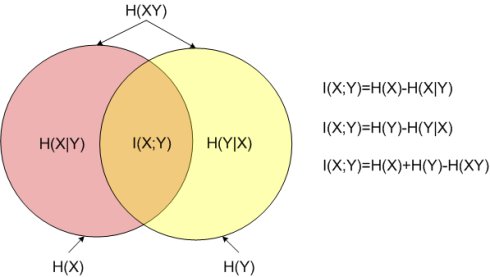
互信息，条件熵，联合熵

看到一个图介绍互信息，条件熵，联合熵，还不错，做个记录：图上的红色和黄色圈分别代表X,Y原始的信息量H(X)/H(Y)/熵值。（注意信息量度量的是一个具体事件发生了所带来的信息，而熵则是在结果出来之前对可能产生的信息量的期望） I(X;Y) : 表示互信息，知道X，Y损失了多少信息量（知道Y，X损失了多少信息量）。 H(X|Y)或H(Y|X): 表示条件熵，知道X，Y还剩多少信息量（H

多级编码情况下各个子信道互信息计算

多级编码情况下各个子信道互信息计算_u011852612的博客-CSDN博客

自信息/熵/联合熵/条件熵/相对熵/交叉熵/互信息及其相互之间的关系

【深度学习基础】：信息论(一)_自信息/熵/联合熵/条件熵/相对熵/交叉熵/互信息及其相互之间的关系_bqw的博客-CSDN博客详解机器学习中的熵、条件熵、相对熵和交叉熵 - 遍地胡说 - 博客园

python计算两个图像的互信息

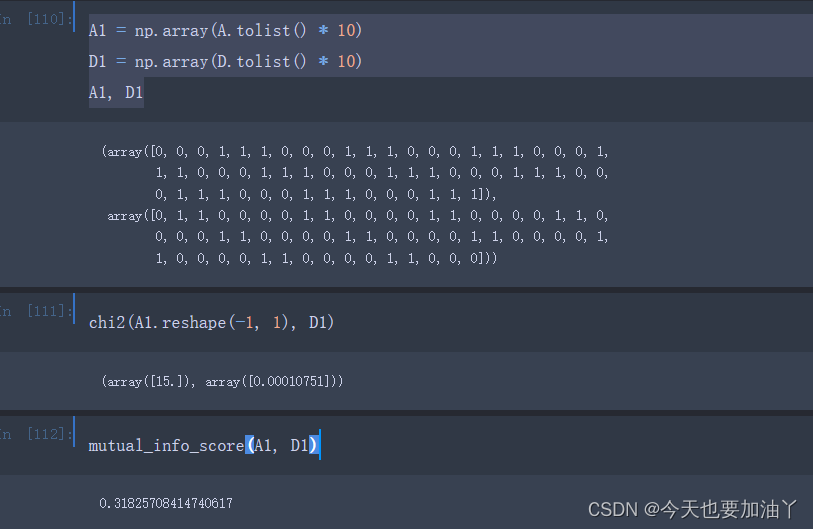
我们常用互信息来衡量两个图像的相似程度。互信息的计算方式如下：使用python中的numpy包或者sklearn可以很方便的计算互信息，计算代码如下： import cv2import numpy as npimport sklearn.metrics as skmdef hxx_forward(x, y):return skm.mutual_info_score(x, y)

文本挖掘预处理之TF-IDF原理 and 互信息的原理

TF-IDF介绍（维基百科）： tf-idf（英语：term frequency–inverse document frequency）是一种用于信息检索与文本挖掘的常用加权技术。tf-idf是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。tf-idf加权的各种形式常

$基于互信息最大化的无监督学习图像特征表示------P02114198田园，P02114018刘颖，P02114050刘欣让$