互信息 java_互信息(Mutual Information)是度量两个事件集合之间的相关性(mutual depe...

互信息(Mutual Information)是度量两个事件集合之间的相关性(mutual dependence)。

平均互信息量定义:

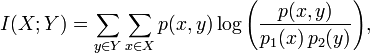
互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。 平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为一个确定的量。

平均互信息量的物理含义

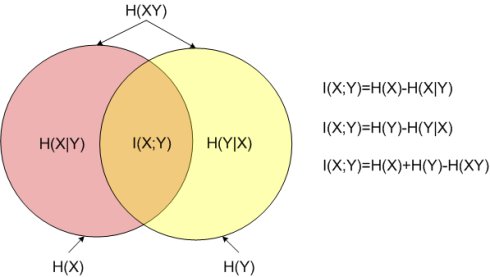
1) 观察者站在输出端：

H(X/Y) —信道疑义度/损失熵.。Y关于X的后验不确定度。表示收到变量Y后,对随机变量X仍然存在的不确定度。代表了在信道中损失的信息。

H(X) —X的先验不确定度/无条件熵。

I(X;Y)—收到Y前后关于X的不确定度减少的量。从Y获得的关于X的平均信息量。

2)观察者站在输入端：

H(Y/X)—噪声熵。表示发出随机变量X后, 对随机变量Y仍然存在的平均不确定度。如果信道中不存在任何噪声, 发送端和接收端必存在确定的对应关系, 发出X后必能确定对应的Y, 而现在不能完全确定对应的Y, 这显然是由信道噪声所引起的。

I(Y;X) —发出X前后关于Y的先验不确定度减少的量.

3)观察者站在通信系统总体立场上：

H(XY)—联合熵.表示输入随机变量X, 经信道传输到达信宿, 输出随机变量Y。即收,发双方通信后,整个系统仍然存在的不确定度.

I(X;Y) —通信前后整个系统不确定度减少量。在通信前把X和Y看成两个相互独立的随机变量, 整个系统的先验不确定度为X和Y的联合熵H(X)+H(Y); 通信后把信道两端出现X和Y看成是由信道的传递统计特性联系起来的, 具有一定统计关联关系的两个随机变量, 这时整个系统的后验不确定度由H(XY)描述。

以上三种不同的角度说明: 从一个事件获得另一个事件的平均互信息需要消除不确定度,一旦消除了不确定度,就获得了信息。

平均互信息量的性质

① 对称性

I(X;Y)= I(Y;X)

由Y提取到的关于X的信息量与从X中提取到的关于Y的信息量是一样的。 I(X;Y)和 I(Y;X)只是观察者的立足点不同。

② 非负性

I(X;Y)≥0

平均互信息量不是从两个具体消息出发, 而是从随机变量X和Y的整体角度出发, 并在平均意义上观察问题, 所以平均互信息量不会出现负值。

或者说从一个事件提取关于另一个事件的信息, 最坏的情况是0, 不会由于知道了一个事件,反而使另一个事件的不确定度增加。

③ 极值性

I(X;Y)≤H(X)

I(Y;X)≤H(Y)

从一个事件提取关于另一个事件的信息量, 至多是另一个事件的熵那么多, 不会超过另一个事件自身所含的信息量。

当X和Y是一一对应关系时: I(X;Y)=H(X), 这时H(X/Y)=0。从一个事件可以充分获得关于另一个事件的信息, 从平均意义上来说, 代表信源的信息量可全部通过信道。

当X和Y相互独立时: H(X/Y) =H(X), I(Y;X)=0。 从一个事件不能得到另一个事件的任何信息,这等效于信道中断的情况。

④ 凸函数性

平均互信息量是p(xi)和p(yj /xi)的函数,即I(X;Y)=f [p(xi), p(yj /xi)];

若固定信道,调整信源, 则平均互信息量I(X;Y)是p(xi)的函数,即I(X;Y)=f [p(xi)];

若固定信源,调整信道, 则平均互信息量I(X;Y)是p(yj /xi)的函数,即I(X;Y)=f [p (yj /xi)]。

平均互信息量I(X;Y)是输入信源概率分布p(xi)的上凸函数(concave function; or convext cap function)。

平均互信息量I(X;Y)是输入转移概率分布p(yj /xi)的下凸函数(convext function; or convext cup function)。

⑤ 数据处理定理

串联信道

在一些实际通信系统中, 常常出现串联信道。例如微波中继接力通信就是一种串联信道.

信宿收到数据后再进行数据处理, 数据处理系统可看成一种信道, 它与前面传输数据的信道构成串联信道。

数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量趋于变小。即

I(X;Z)≤I(X;Y)

I(X;Z)≤I(Y;Z)

其中假设Y条件下X和Z相互独立。

两级串联信道输入与输出消息之间的平均互信息量既不会超过第Ⅰ级信道输入与输出消息之间的平均互信息量,也不会超过第Ⅱ级信道输入与输出消息之间的平均互信息量。

当对信号/数据/消息进行多级处理时, 每处理一次, 就有可能损失一部分信息, 也就是说数据处理会把信号/数据/消息变成更有用的形式, 但是绝不会创造出新的信息。这就是所谓的信息不增原理。

当已用某种方式取得Y后, 不管怎样对Y进行处理, 所获得的信息不会超过I(X;Y)。每处理一次, 只会使信息量减少, 至多不变。也就是说在任何信息流通系统中, 最后获得的信息量,至多是信源提供的信息。一旦在某一过程中丢失了一些信息, 以后的系统不管怎样处理, 如果不能接触到丢失信息的输入端, 就不能再恢复已丢失的信息。