本文主要是介绍拿捏!相关性分析,一键出图!皮尔逊、斯皮尔曼、肯德尔、最大互信息系数(MIC)、滞后相关性分析,直接运行!独家可视化程序!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
适用平台:Matlab2020及以上
相关性分析是一种统计方法,用于衡量两个或多个变量之间的关系程度。通过相关性分析,我们可以了解变量之间的相互关系、依赖性,以及它们是如何随着彼此的变化而变化的。相关性分析通常包括计算相关系数或其他衡量关联度的指标。
①量化特征之间的关联程度:通过相关系数的值,我们可以判断它们的关系是强烈的、中等还是弱。
②特征降维:在大规模数据集中,相关性分析可以帮助我们过滤掉与目标序列关系较弱的变量,从而聚焦于关键的特征。
降维的方法:皮尔逊(Pearson)、斯皮尔曼(Spearman)、肯德尔(Kendall)、最大互信息系数(MIC)、滞后相关性。分别绘制出相关性矩阵,并且矩阵中每个值我们都用饼图表示,看着更加高大上!加深审稿人对文章的好感。
下面分别介绍这几种相关性分析的特点:
皮尔逊相关系数:皮尔逊相关系数衡量的是两个变量之间的线性关系。它通过计算协方差和两个变量的标准差来完成。皮尔逊相关系数在处理线性关系强的数据时非常有效,取值范围在 -1 到 1 之间,正值表示正相关,负值表示负相关,0 表示无关。

斯皮尔曼相关系数:斯皮尔曼相关系数是一种基于秩次的非参数方法,用于衡量两个变量之间的单调关系。首先将变量的原始数据转化为秩次,然后计算秩次的皮尔逊相关系数。适用于非线性关系,对异常值不敏感,取值范围也在 -1 到 1 之间。
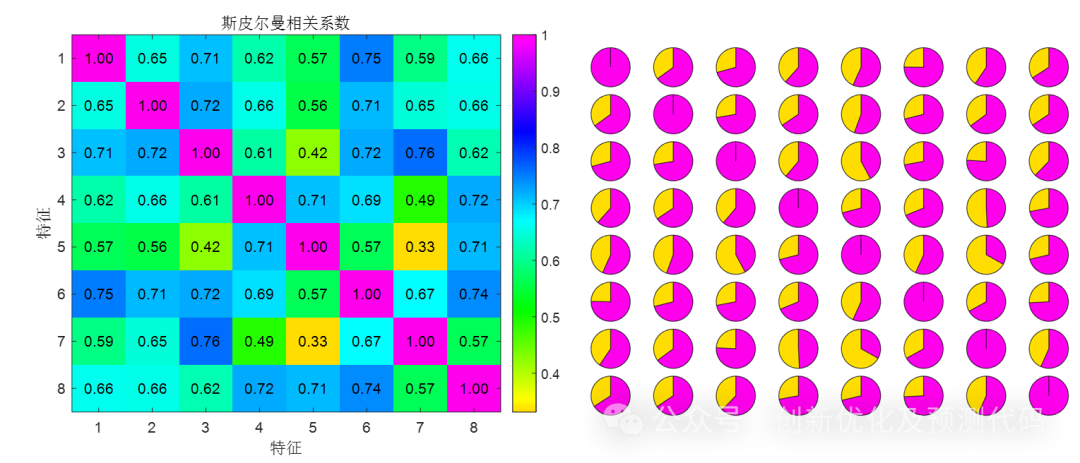
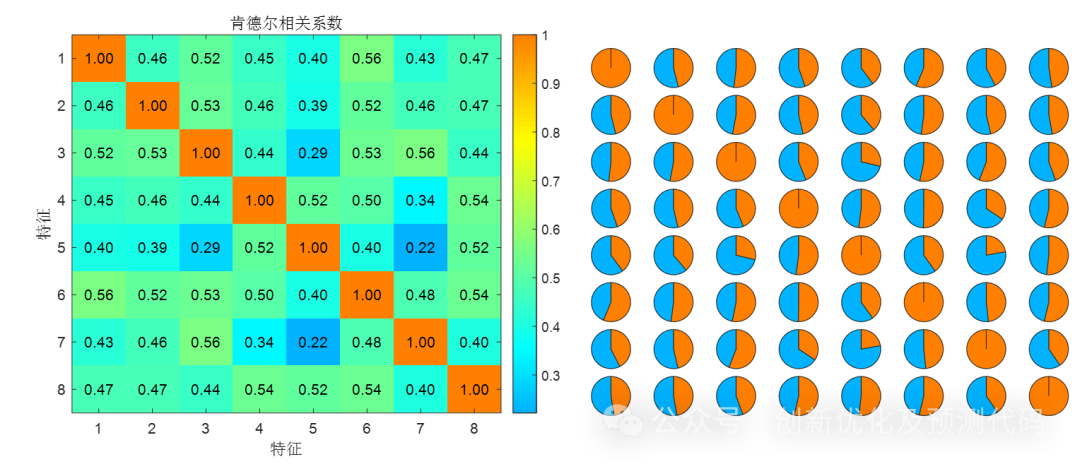
肯德尔相关系数:计算过程类似斯皮尔曼相关系数,肯德尔相关系数也是基于秩次的非参数方法。它测量的是两个变量的等级之间的一致性程度,而不是直接测量它们的秩次之间的线性关系。适用于非线性关系,对异常值不敏感,常用于秩次数据的相关性分析。
最大互信息系数(MIC):最大互信息系数是一种非参数方法,用于测量两个变量之间的非线性关系。它通过将数据空间划分为网格,并计算每个网格中的互信息来完成。对于非线性关系的探测性能较好,但计算较复杂。

滞后相关性:滞后相关性衡量的是两个变量之间在时间上的延迟关系。通过计算变量在不同时间点上的相关性来确定它们是否存在滞后关系。适用于时间序列数据,能够揭示时间上的因果关系。

总结:上述方法都有其适用的场景和局限性。选择哪种方法取决于你们的数据特点以及你的侧重点问题。线性相关性可以使用皮尔逊相关系数,非线性或秩次相关性可以考虑斯皮尔曼和肯德尔相关系数。滞后相关性适用于时间序列数据,而MIC较适合处理非线性关系。
部分代码:
%% 计算互相关系数(滞后相关性)% 来自公众号《创新优化及预测代码》
n2=10; %滞后时序
y=data(:,end);
x=data(:,1:end-1);
%计算x在滞后或超前0-10个时段下与y的相关性
for i=1:size(x,2)croc(:,i)=crosscorr(y,x(:,i),'NumLags',n2);
end
croc=croc';% croc中行表示变量,列表述滞后序列-n2,-n2+1,...,0,1,...,n2-1,n2 下的x与y的相关系数%% 绘制热力图
[N, D]=size(data);%% 皮尔逊相关系数 % 来自公众号《创新优化及预测代码》
% 绘制皮尔逊相关系数二维图,使用hsv颜色映射
figure;
imagesc(pearson_corr);
colorbar;
% 颜色映射
color = hsv(200);
colormap(color(30:end-30,:));
title('皮尔逊相关系数');
xlabel('特征');
ylabel('特征');% 在图中添加皮尔逊相关系数的标签
for i = 1:size(pearson_corr, 1)for j = 1:size(pearson_corr, 2)text(j, i, num2str(pearson_corr(i, j), '%.2f'), 'Color', 'k', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle');end
end% 饼图 % 来自公众号《创新优化及预测代码》
pieplot(pearson_corr);
colormap(color(30:end-30,:));%% 绘制肯德尔相关系数二维图,使用Jet颜色映射 % 来自公众号《创新优化及预测代码》
figure;
imagesc(kendall_corr);
colorbar;
color = jet(200);
colormap(color(60:end-50,:));
title('肯德尔相关系数');
xlabel('特征');
ylabel('特征');% 在图中添加肯德尔相关系数的标签
for i = 1:size(kendall_corr, 1)for j = 1:size(kendall_corr, 2)text(j, i, num2str(kendall_corr(i, j), '%.2f'), 'Color', 'k', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle');end
end% 饼图
pieplot(kendall_corr);
colormap(color(60:end-50,:));这篇关于拿捏!相关性分析,一键出图!皮尔逊、斯皮尔曼、肯德尔、最大互信息系数(MIC)、滞后相关性分析,直接运行!独家可视化程序!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





