特征选择-皮尔逊相关系数-互信息

特征选择
1.相关性
通过使用相关性，我们很容易看到特征之间的线性关系。这种关系可以用一条直线拟合。

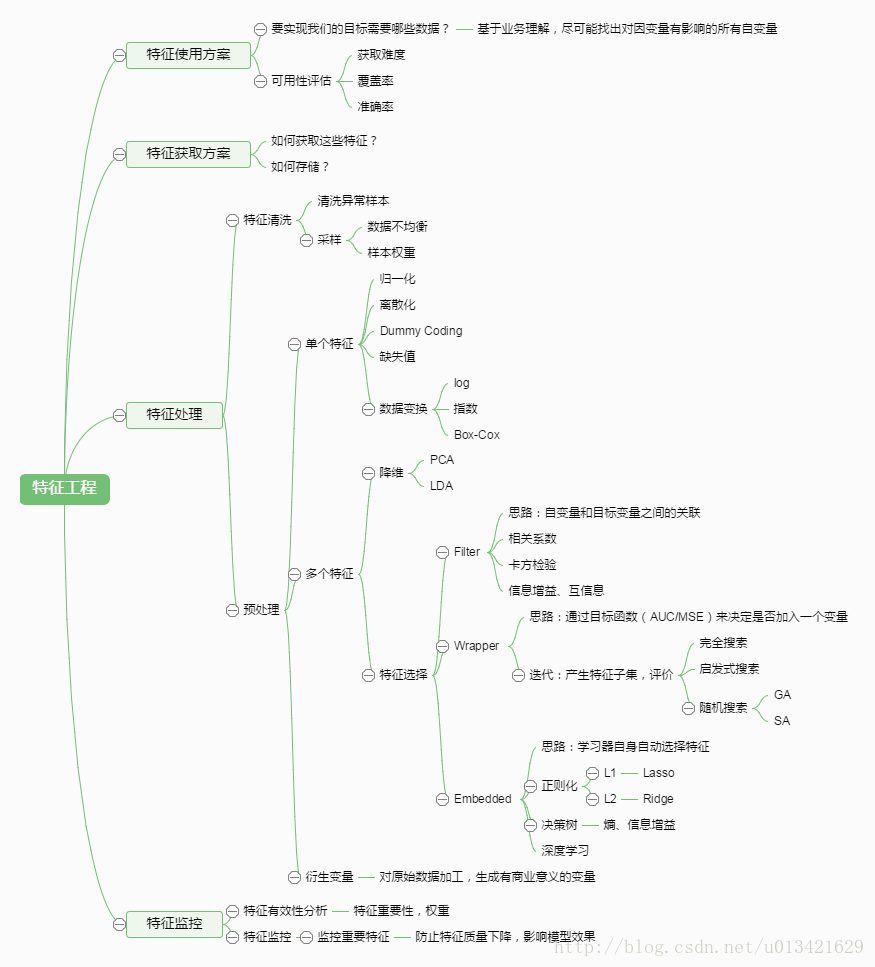
下面通过皮尔逊相关系数（Pearson correlation coefficient）来解释特征的相关性：
下面每幅图上方的相关系数Cor(X1, X2)是计算出来的皮尔逊r值，从图中可以看出不同程度的相关性。

scipy.stats.pearsonr()，给定两个数据序列 ，会返回相关系数值和p值所组成的元组。皮尔逊相关系数（皮尔逊r值）测量两个序列的线性关系，取值在-1到1之间，-1代表负相关、1代表正相关、0代表不相关。r值：

上式中m_x是向量x的均值，m_y是向量y的均值。

In [1]: from scipy.stats import pearsonrIn [2]: pearsonr([1,2,3], [1,2,3.1])
Out[2]: (0.9996222851612184, 0.017498096813278487)

上图中，前三个具有高相关系数，我们可以选择把X1或者X2扔掉，因为他们似乎传递了相似的信息。
然而在最后一种情况，我们应该把两个特征都保留。
基于相关性的特征选择方法的一个最大的缺点就是，它只检测出线性关系（可以用一条直线拟合的关系）。下图形象的展示出了相关性的缺陷：

对于非线性关系，互信息出马了。

2.互信息
在进行特征选择时，我们不该把焦点放在数据关系的类型（线性关系）上，而是要考虑在已经给定另一个特征的情况下一个特征可以提供多少信息量。
互信息会通过计算两个特征所共有的信息，把上述推理工程形式化表达出来。与相关性不同，它依赖的不是数据序列，而是数据的分布。

先看一下香农(Claude Shannon）的信息熵(Entropy H(X) ):

现在，如果这个硬币不是公平的，旋转后有60%的可能性会出现硬币的正面：

*我们可以看到这种情形有较少的不确定性。不管正面出现的概率为0%还是100%，不确定性都将会远离我们在0.5时时所得到的熵，到达极端的0值，如下图所示：

这样我们就可以得到一个特征使另一个特征的不确定性减少的程度。

互信息量

归一化的互信息量

import numpy as np
from scipy.stats import entropydef mutual_info(x, y, bins=10):counts_xy, bins_x, bins_y = np.histogram2d(x, y, bins=(bins, bins))counts_x, bins = np.histogram(x, bins=bins)counts_y, bins = np.histogram(y, bins=bins)counts_xy += 1counts_x += 1counts_y += 1P_xy = counts_xy / np.sum(counts_xy, dtype=float)P_x = counts_x / np.sum(counts_x, dtype=float)P_y = counts_y / np.sum(counts_y, dtype=float)I_xy = np.sum(P_xy * np.log2(P_xy / (P_x.reshape(-1, 1) * P_y)))return I_xy / (entropy(counts_x) + entropy(counts_y))

互信息的一个较好的性质在于，跟相关性不同，它并不只关注线性关系。如下图所示：


我们需要计算每一对特征之间的归一互信息量。对于具有较高互信息量的特征对，我们会把其中一个特征扔掉。在进行回归的时候，我们可以把互信息量非常低的特征扔掉。
对于较小的特征集合这种方式的效果或许还可以。但是，在某种程度上，这个过程会非常缓慢，计算量会以平方级别增长，因为我们要计算的是每对特征之间的互信息量。
其他特征选择方法

1. 内嵌于机器学习模型中的：
   决策树。——有一个甚至于其内核的特征选择机制。
2. 一些正则化方法：
   对模型复杂性进行惩罚，从而使学习过程朝效果较好而且仍然“简单”的模型发展。
   L1正则化。——把效用不大的特征的重要性降低为0，然后把他们扔掉进行特征选择。