nlogn专题

算法-排序算法：堆排序（HeapSort ）【O(nlogn)】

MyArray.java /*** 数组** @author* @version 2018/8/4*/public class MyArray<E> {private E[] arr;private int size;public MyArray(int capacity){arr = (E[])new Object[capacity];size = 0;}public MyArray() {

#1128 : 二分·二分查找（两种方法先排序在二分O(nlogN） + 直接二分+快排思想O(2N) ）

#1128 : 二分·二分查找时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 Nettle最近在玩《艦これ》，因此Nettle收集了很多很多的船(这里我们假设Nettle氪了很多金，开了无数个船位)。去除掉重复的船之后，还剩下N(1≤N≤1,000,000)种不同的船。每一艘船有一个稀有值，任意两艘船的稀有值都不相同，稀有值越小的船越稀

UVA 10354 nlogn LIS

nlogn的最长上升子序列（原理）。这是第一个trick。第二个，要左边和右边的相同，枚举每一个点作为最高点时的情况。两边取较小的那个再乘以2。 #include<stdio.h>#include<string.h>#include<algorithm>using namespace std;#define MS(x) memset(x,0,sizeof(x))int up[

如何理解快速排序的时间复杂度是O(nlogn)

选择排序、冒泡排序等算法的时间复杂度都比较好理解，但不是很清楚快速排序的时间复杂度为什么是O(nlogn)。从《算法图解》中看到的思路，很赞，解决了一直以来的疑惑。引用自《算法图解》：快速排序的情况比较棘手，在最糟情况下，其运行时间为O(n2)。。在平均情况下，快速排序的运行时间为O(nlogn)。 1、平均情况与最糟情况快速排序的性能高度依赖于你选择的基准值。最糟情况假设你总

单调递增最长子序列 O(nlogn)

单调递增最长子序列时间限制： 3000 ms | 内存限制： 65535 KB 难度： 4 描述求一个字符串的最长递增子序列的长度如：dabdbf最长递增子序列就是abdf，长度为4 输入第一行一个整数0<n<20,表示有n个字符串要处理随后的n行，每行有一个字符串，该字符串的长度不会超过10000 输出输出字符串的最长递增子序列的长度样例输入

LCS时间复杂度O(NlogN) （LCS 转 LIS）

LCS(Longest Common Subsequences)最长公共子序列用一般的动态规划时间复杂度O(N^2), 但经过优化可以达到O(NlogN),下面是转载集训队某人的最长递增子序列解题报告。　　先回顾经典的O(n^2)的动态规划算法，设A[i]表示序列中的第i个数，F[i]表示从1到i这一段中以i结尾的最长上升子序列的长度，初始时设F[i] = 0(i =

【算法基础】o(1), o(n), o(logn), o(nlogn)

由于平时接触算法比较少，今天看资料看到了o(1)，都不知道是什么意思，百度之后才知道是什么意思。描述算法复杂度时,常用o(1), o(n), o(logn), o(nlogn)表示对应算法的时间复杂度，是算法的时空复杂度的表示。不仅仅用于表示时间复杂度，也用于表示空间复杂度。 O后面的括号中有一个函数，指明某个算法的耗时/耗空间与数据增长量之间的关系。其中的n代表输入数据

LeetCode 2007.从双倍数组中还原原数组：哈希表——从nlogn到n

【LetMeFly】2007.从双倍数组中还原原数组：哈希表——从nlogn到n 力扣题目链接：https://leetcode.cn/problems/find-original-array-from-doubled-array/ 一个整数数组 original 可以转变成一个双倍数组 changed ，转变方式为将 original 中每个元素值乘以 2 加入数组中，然后将所有元素

(nlogn求LIS，确定状态唯一性）LIS of Sequence CodeForces - 486E

The next “Data Structures and Algorithms” lesson will be about Longest Increasing Subsequence (LIS for short) of a sequence. For better understanding, Nam decided to learn it a few days before the les

leetcode-300 最长上升子序列 O(NlogN)解法

1. 题目内容给定一个无序的整数数组，找到其中最长上升子序列的长度。示例: 输入: [10,9,2,5,3,7,101,18] 输出: 4 解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。说明: 可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。你算法的时间复杂度应该为 O(n2) 。进阶: 你能将算法的时间复杂度降低到 O(n log n

最长递增子序列（LIS）的O(NlogN)打印算法

题目：求一个一维数组arr[n]中的最长递增子序列的长度，如在序列1,5,8,3,6,7中，最长递增子序列长度为4 (即1,3,6,7)。由于LIS用O(NlogN)也能打印，O(N^2)的DP方法见最后。从LIS的性质出发，要想得到一个更长的上升序列，该序列前面的数必须尽量的小。对于原序列1,5,8,3,6,7来说，当子序列为1,5,8时，遇到3时，序列

POJ3666 nlogn 做法

呜呜呜我再也不会放弃一个我能理解的题了！就算花几个小时！就算手里还有很多题！给你一个序列，每次操作你可以让一个数加一或者让一个数减一，问使这个序列不减的最小操作数（具体是啥我也不想看了，大概就是这样,如果是严格递增a[i] - i就变成了不减）然后有一个结论是改变之后的序列的每个数，一定是原来序列中的某个数。那么离散化之后的n ^２ DP就很显然了但是！！有一个极其巧妙的nlogn的解

O(nlogn)~O(1)的LCA

RT，这个算法感觉超级有用大概就是说搞出来欧拉序（欧拉序就是每个点进入时记录一次，从每一个子树出来时记录一次）然后再欧拉序上搞RMQ，就可以了，具体可以自己画个图看看这东西超级好写的，常数又小代码： #include<cstdio>#include<cstring>#include<iostream>#include<cmath>#include<algorithm>

【BestCoder Round 65C】【树状数组动态查找第k大 O(nlogn)】ZYB's Premutation 告诉你前i个数中的逆序对数让你还原全排列

ZYB's Premutation Accepts: 218 Submissions: 983 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) 问题描述 ZYBZYB有一个排列PP,但他只记得PP中每个前缀区间的逆序对数,现在他要求你还原这

最长上升子序列 O(nlogn)

给定一个数列arr[]={5,2,1,4,5,3}; 定义一个数组dp，dp[0]初始化为最小值（小于arr的最小值），定义top指向dp数组最后一个元素，定义i=0为arr数组指针；从数组arr中取第一个数(value1)，与dp数组最后一个数(value2)比较；若value1>value2，则将value1插入到dp数组最后一位，dp数组长度+1（dp[++top]=arr[i]），反之，

归并排序 O(nlogn)

该算法是采用分治法的一个非常典型的应用。归并排序可以理解为反复调用二路归并算法而实现的。所谓二路归并，就是将两个有序序列合并成为一个有序序列。二路归并属于迭代式算法。每次迭代需要比较两个待合并序列的首元素，将小者取出添加至新序列的末尾。如此反复，直到一序列为空。最后，将另一非空的序列整体接至输出向量的末尾。 #include <bits/stdc++.h>using namespace

300. 最长递增子序列动态规划O(n2) 贪心+二分 O(nlogn)

思路动态规划，定义状态 d p [ i ] dp[i] dp[i]代表以 n u m s [ i ] nums[i] nums[i]结尾的最长递增子序列的长度，这样的话 d p [ i ] dp[i] dp[i]和其子问题 d p [ k ] , 0 < = k < i dp[k],0<=k<i dp[k],0<=k<i便产生了联系、状态转移方程 d p [ i ] = m a x ( d

例题27 UVa10635 Prince and Princess（DP：LIS的nlogn算法）

题意：看白书要点：这题本来应该是LCS，但因为时间的要求，可以转化为LIS，而且还得用nlogn的算法，基本思路就是用b数组来存储当前b的值在a数组中对应的位置。LIS的nlogn算法的思路就是，每次用g来存储，并每次在其中进行二分查找，注意这里每次更新是不会改变LIS的性质的，最后g的结果不是所需的LIS，这里要注意一下。 #include<iostream>#include

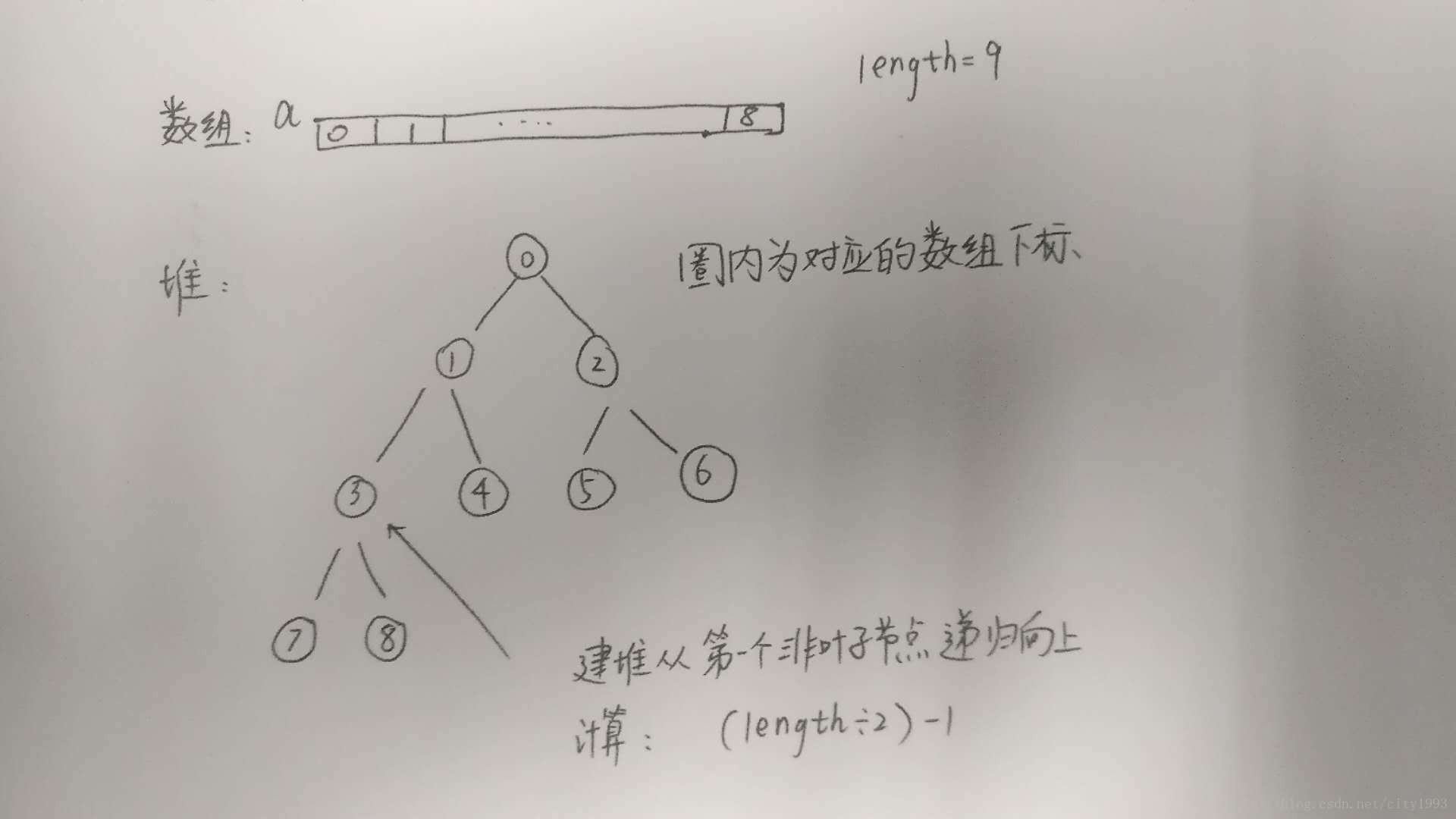
堆排序复杂度为O(nlogn)，需要注意的误区

时间复杂度为 O(nlogn) 的排序算法

归并排序归并排序遵循分治的思想：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后合并这些子问题的解来建立原问题的解，归并排序的步骤如下：划分：分解待排序的 n 个元素的序列成各具 n/2 个元素的两个子序列，将长数组的排序问题转换为短数组的排序问题，当待排序的序列长度为 1 时，递归划分结束合并：合并两个已排序的子序列得出已排序的最终结果归并排序

POJ 1631 Bridging signals 最长上升子序列小结 LIS的O(nlogn)算法

POJ 1631 Bridging signals 题目分析：题目要求避免相交，则可转化为对给定的序列求最长上升子序列。首先使用了dp来求解，复杂度为O(n*n)，在题目的数据范围下超时了… #include<iostream>#include<stdio.h>#include<algorithm>using namespace std;int dp[40000];int nu

算法学习—算法运行时间、logN、NlogN

1大部分程序的大部分指令之执行一次，或者最多几次。如果一个程序的所有指令都具有这样的性质，我们说这个程序的执行时间是常数。logN 如果一个程序的运行时间是对数级的，则随着N的增大程序会渐渐慢下来，如果一个程序将一个大的问题分解成一系列更小的问题，每一步都将问题的规模缩减成几分之一，一般就会出现这样的运行时间函数。在我们所关心的范围内，可以认为运行时间小于一个大的常数。对数的基数会影响这个常数，但