堆排序复杂度为O(nlogn)，需要注意的误区

本文希望阐述堆排序O(nlogn)的一些关键细节，摘录一篇博文O(n^2)进行比较。

用作比较的原文 版权声明：为者常成，行者常至

堆排序的特点是优化后的选择排序，其时间复杂度为O(nlogn),下面第一段代码的做法比这个复杂度要高。原因在下文阐述。

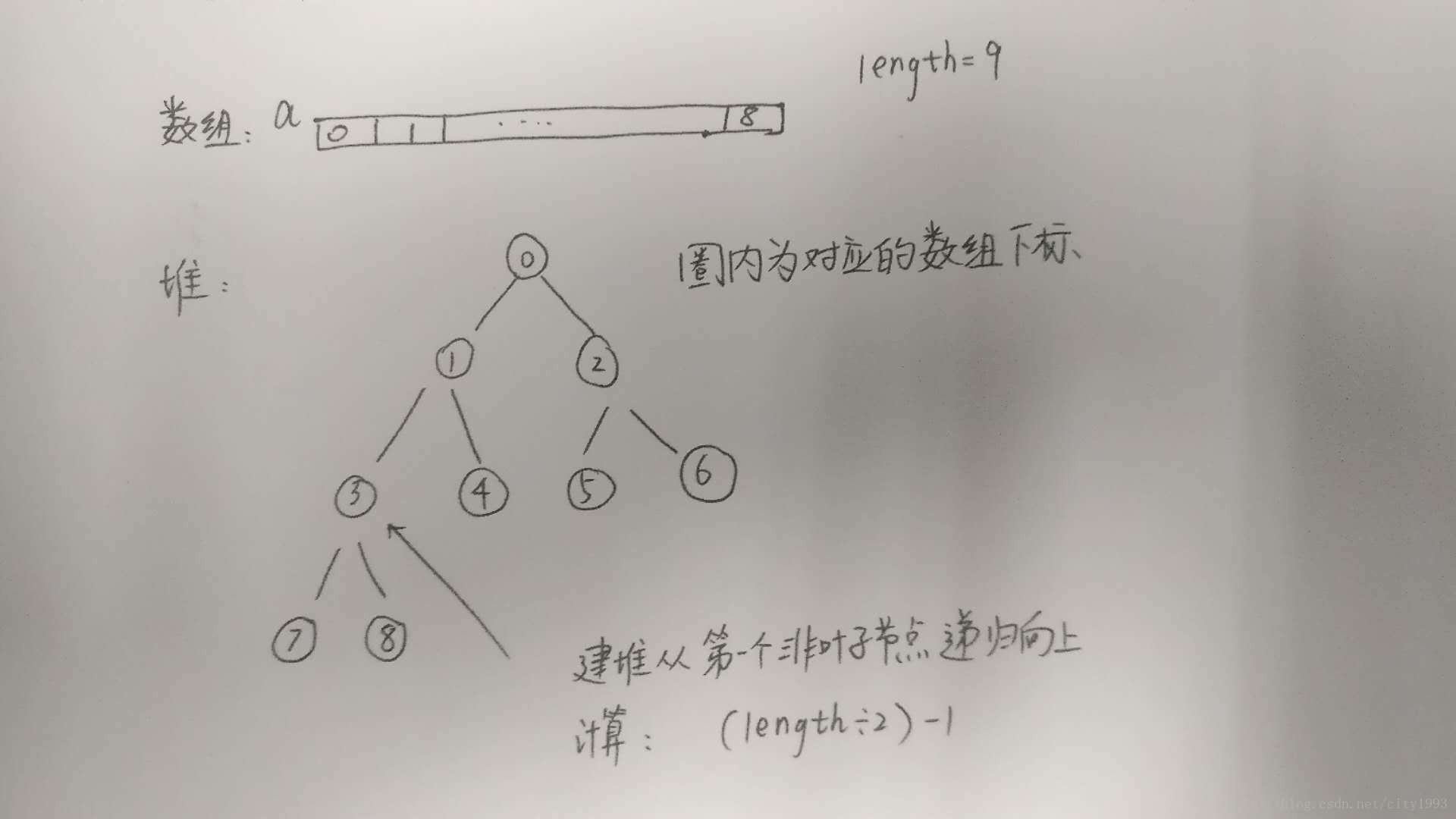
堆排序将要排序的对象看做一颗完全二叉树，数据结构可以用数组来实现。

 初始化建堆过程时间：O(n)                                    更改堆元素后重建堆时间：O(nlogn)                                                                         

具体证明可见：http://blog.csdn.net/yuzhihui_no1/article/details/44258297

下面的做法是在建好堆之后，交换堆顶和堆底之后，又执行了重建堆的过程。复杂度应该为O(n^2)。

待比较程序代码如下:

package ex;
import java.util.Arrays;public class Sort {public static void main(String args[]) {  int []a = new int[] {16,25,34,27,30,5,7,4,41,55};Sort.heapSort(a);System.out.println(Arrays.toString(a));}static int parent(int i) {return (i - 1)/2;}static int left(int i) {return 2*i + 1;}static int right(int i) {return 2*i + 2;}static void maxHeapfy(int []a,int i,int heapSize) {   //数组a，第i个结点，heapSize是数组种实际要排序的元素的长度int left = left(i);     //有的时候能够递归到叶子结点，叶子结点无后继，下面两个if都注意到了这一点int right = right(i);   int largest = i;if(left < heapSize && a[left] > a[largest]) {   //largest = left;}if(right < heapSize && a[right] > a[largest])  {largest = right;}if(largest != i) {      //把最大值给父结点a[largest] = a[largest] ^ a[i];a[i] = a[largest] ^ a[i];a[largest] = a[largest] ^ a[i];maxHeapfy(a,largest,heapSize);    //发生交换之后还要保证大根堆性质}}static void buildMaxHeap(int []a,int heapSize) {for(int i = (heapSize-1)/2;i >= 0;i--) {  //此处计算非叶子节点时和计算父节点混淆maxHeapfy(a,i,heapSize);              //此处调用重建堆的过程增加了时间复杂度}}static void heapSort(int []a) {for(int i = a.length-1;i > 0;i--) {buildMaxHeap(a,i+1);   //堆的大小从n到2a[i] = a[0] ^ a[i];    //交换a[0] = a[0] ^ a[i];a[i] = a[0] ^ a[i];}}
}
//输出结果:
//[4, 5, 7, 16, 25, 27, 30, 34, 41, 55]

改进的重建堆的过程

public class HeapSorter implements Sorter{/* (non-Javadoc)* @see A4.Sorter#sort(java.lang.Comparable[])*/@Overridepublic void sort(Comparable[] data) {buildMaxHeap(data,data.length);}int parent(int i){return (i-1)/2;}int left(int i){return 2*i+1;}int right(int i){return 2*i+2;}/*** 将堆排序选出的最大的元素放到数组的最后位置。* 下午10:38:26* 2017年11月29日* @author city*/private void buildMaxHeap(Comparable[] data, int heapSize) {// First Step build Max-heapfor(int i = heapSize/2-1;i>=0;i--) {maxHeapfy(data,i,heapSize);}for(int i = data.length-1;i>0;i--){Comparable tmp = data[i];data[i] = data[0];data[0] = tmp;maxHeapfy(data, 0, i);}}/*** 堆排序算法核心，建立最大堆。* 下午10:39:54* 2017年11月29日* @author city*/private void maxHeapfy(Comparable[] data, int i, int heapSize) {// TODO Auto-generated method stubint left = left(i);int right = right(i);int largest = i;if(left<heapSize && data[left].compareTo(data[largest])>0){largest = left;}if(right<heapSize && data[right].compareTo(data[largest])>0){largest = right;}if(largest!=i){Comparable tmp = data[largest];data[largest] = data[i];data[i] = tmp;maxHeapfy(data, largest, heapSize);}}	
}

比较原文转载自http://blog.csdn.net/qq_35178267/article/details/78313306#insertcode

如有侵权请联系