本文主要是介绍最长上升子序列 O(nlogn),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
给定一个数列arr[]={5,2,1,4,5,3};
- 定义一个数组dp,dp[0]初始化为最小值(小于arr的最小值),定义top指向dp数组最后一个元素,定义i=0为arr数组指针;
- 从数组arr中取第一个数(value1),与dp数组最后一个数(value2)比较;
- 若value1>value2,则将value1插入到dp数组最后一位,dp数组长度+1(dp[++top]=arr[i]),反之,从dp数组中用二分查找找出第一个大于value1的位置k,用vaule1替换(dp[k]=arr[i])。arr数组指针右移(i++);
- 重复2、3两步,直到arr数组指针指向最后一位,top的值就是最长上升子序列的长度;
图解(红色箭头为top,蓝色箭头在arr中表示数组指针i,在dp中表示value1在dp中的位置):
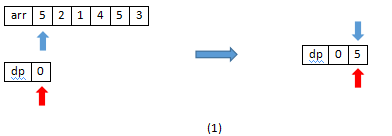
value1=5,value2=0,value1>value2,将value1插入到dp数组最后一位,top=1;

value1=2,value2=5,value1<value2,dp数组从左到右第一个大于value1的值为5(k=1),将dp数组中的5用2替换(dp[1]=value1);
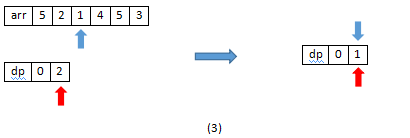
value1=1,value2=2,value1<value2,dp数组从左到右第一个大于value1的值为2(k=1),将dp数组中的2用1替换(dp[1]=value1);

value1=4,value2=1,value1>value2,将value1插入到dp数组最后一位,top=2;
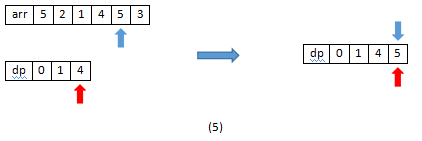
value1=5,value2=4,value1>value2,将value1插入到dp数组最后一位,top=3;

value1=3,value2=5,value1<value2,dp数组从左到右第一个大于value1的值为4(k=2),将dp数组中的4用3替换(dp[2]=value1);
至此arr数组指针指向了最后一位,最长上升子序列的长度为top=3;
注意:dp[0]的值应根据题目情况而定,在不知道arr中的最小值的情况下,通常将dp[0]设置为INT_MIN;
代码:
#include<iostream>
#include<climits>
using namespace std;
const int N = 100005;
int dp[N];
int arr[N];
int BinSearch(int sta,int end,int key)//二分查找,返回第一个比key大的值的位置
{while(sta<=end){if(sta==end)return sta;int mid=(sta+end)>>1;if(dp[mid]<key)sta=mid+1;elseend=mid;}return 0;
}
int main()
{int n;cout<<"输入arr数组长度:"<<endl; scanf("%d",&n);cout<<"输入arr数组的内容:"<<endl; for(int i=0;i<n;i++)scanf("%d",&arr[i]);dp[0]=INT_MIN; //dp[0]初始化为最小 int top=0; //top指向dp数组最后一位 for(int i=0;i<n;i++) //遍历arr数组 {if(arr[i]>dp[top]) //大于dp数组最后一位为true dp[++top]=arr[i]; //插入到dp数组最后一位,top+1 else{int k=BinSearch(1,top,arr[i]); //从dp数组中找出第一个大于arr[i]的位置k dp[k]=arr[i]; //用arr[i]替换dp[k]的值 }}printf("arr数组最长上升子序列的长度为:%d\n",top);return 0;
}
这篇关于最长上升子序列 O(nlogn)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





