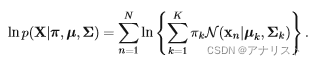maximization专题

序列化推荐的图模型——Selecting Sequences of Items via Submodular Maximization（更新中）

本文介绍一种基于图模型的序列化推荐方法：OMEGA。文章来自AAAI-17，题目为《Selecting Sequences of Items via Submodular Maximization》，作者是来自苏黎世联邦理工学院的Sebastian Tschiatschek，Adish Singla 以及Andreas Krause。背景子集选择问题首先，介绍一下子集选择问题，该问题的

Influence blocking maximization on networks: Models, methods and applications

abstract 由于各种社会和贸易网络的不断出现，网络影响力分析引起了研究者的极大兴趣。基于不同的影响力传播模型，人们提出了许多网络影响力最大化的新模型和方法。作为传统影响力最大化问题的延伸和扩展，影响力封锁最大化问题已成为研究热点，并在物理学、计算机科学和流行病学等多个领域得到广泛应用。近年来，已经报道了影响块最大化问题的各种方法。然而，我们仍然缺乏从社交网络影响力分析方面系统

统计计算二|EM算法（Expectation-Maximization Algorithm，期望最大化算法）

系列文章目录统计计算一|非线性方程的求解文章目录系列文章目录一、基本概念（一）极大似然估计和EM算法（二）EM算法的基本思想（三）定义1、缺失数据, 边际化和符号2、Q函数3、混合高斯模型（Gaussian Mixture Model，简称GMM）4、一般混合模型三、收敛性（一）琴生不等式（Jensen’s inequality）（二） EM 算法的收敛性质（三）MM 算法 (

期望最大化算法(expectation maximization,EM)

EM算法是一种迭代算法，用于含有隐变量(hidden variable)或缺失数据(incomplete-data)的概率模型参数的极大似然估计。EM算法被广泛用于高斯混合模型(Guassian Mixture Model,GMM)和隐马尔可夫模型(Hidden Markov Model,HMM)的参数估计。每次迭代分为两步：E步，求期望；M步，求极大。概率模型有时既包含观测变量(observab

Influence maximization on temporal networks: a review

Abstract 影响力最大化（IM）是网络科学中的一个重要主题，其中选择一个小的种子集来最大化网络影响力的传播。最近，这个问题引起了网络结构随时间变化的时间网络的关注。这种动态变化的网络上的 IM 是本次评论的主题。我们首先将方法分为两个主要范式：单播种和多播种。在单次播种中，节点在扩散过程开始时激活，大多数方法要么有效地估计影响力扩散并使用贪婪算法选择节点，要么使用节点排名启发式。

Codeforces 1133 problem D Zero Quantity Maximization —— 求a*k=b的最大数量

You are given two arrays a and b, each contains n integers. You want to create a new array c as follows: choose some real (i.e. not necessarily integer) number d, and then for every i∈[1,n] let ci:=d

A Community-Aware Framework for Social Influence Maximization

Abstract 我们考虑影响力最大化（IM）问题，即在社交网络中选择 k 个种子节点，以使受影响的节点的预期数量最大化的任务。我们提出了一个社区意识分而治之的框架，其中包括（i）学习社交网络的固有社区结构，（ii）通过解决每个社区的影响力最大化问题来生成候选解决方案，以及（iii）选择最终的解决方案使用新颖的渐进预算方案的种子节点集。我们对现实世界社交网络的实验表明，

[分布外检测]Entropy Maximization and Meta Classification for Out-of-Distribution Detection...实现记录

Aomaly Segmentation 项目记录该文档记录异常检测在自动驾驶语义分割场景中的应用。主要参考论文Entropy Maximization and Meta Classification for Out-of-Distribution Detection in Semantic Segmentation 摘要： Deep neural networks (DNNs) for

Capacity Maximization for Movable Antenna Enabled MIMO Communication

文章目录 II. SYSTEM MODEL AND PROBLEM FORMULATIONC. Problem Formulation III. PROPOSED ALGORITHMA. Alternating OptimizationB. Solution for Problem (P2-m) APPENDIX II. SYSTEM MODEL AND PROBLEM FORM

OpenCV（3）ML库-Expectation - Maximization 算法

最大期望算法（Expectation-maximization algorithm，又译期望最大化算法）在统计中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。在统计计算中，最大期望（EM）算法是在概率（probabilistic）模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量（Latent Variable）

Codeforces Round #544 (Div. 3) D. Zero Quantity Maximization(思维)

题目链接：http://codeforces.com/contest/1133/problem/D 题意：是输入一个n，加下来分别输入n个a[i]和b[i]，现在让你找一个d，现在要求一个c数组，c[i] = d * a[i] + b[i]，也就是找一个d使得c数组中有最多的0，问最多的0的个数为多少。思路：对b[i] / a[i]化成最简分数，用map存一下分数，最大的分数个数就是答案。需

EM算法(expectation maximization algorithms)揭秘

EM算法篇 EM算法简介 EM算法，也叫expectation maximization algorithms，是在包含隐变量(未观察到的潜在变量)的概率模型中寻找参数最大似然估计(也叫最大后验估计)的迭代算法。EM 算法在期望 (E步骤) 和最大化 (M步骤) 之间交替执行，前者计算模型参数当前估计的对数似然期望函数，后者对E步骤中找到的预期对数似然计算最大化，然后使用参数新估计值来确定下一

【深度学习】卷积神经网络的可视化---Visualization by activation Maximization

The Overview: Activation Maximization (AM)是用来可视化各个卷积层的输入偏好。通过观测输入偏好，我们可以更好的了解CNN的卷积层到底学习到了什么。卷积学习得到的特征可以通过一帧合成图像来最大化神经元的激活。为了合成这个输入偏好，我们可以通过对CNN的输入像素进行反复迭代来最大化神经元的激活。换言之，我们可以通过合成一个输入样式来激活神经元，使得神经元

Sum Rate Maximization for IRS-Assisted Uplink NOMA（论文分析）（一）

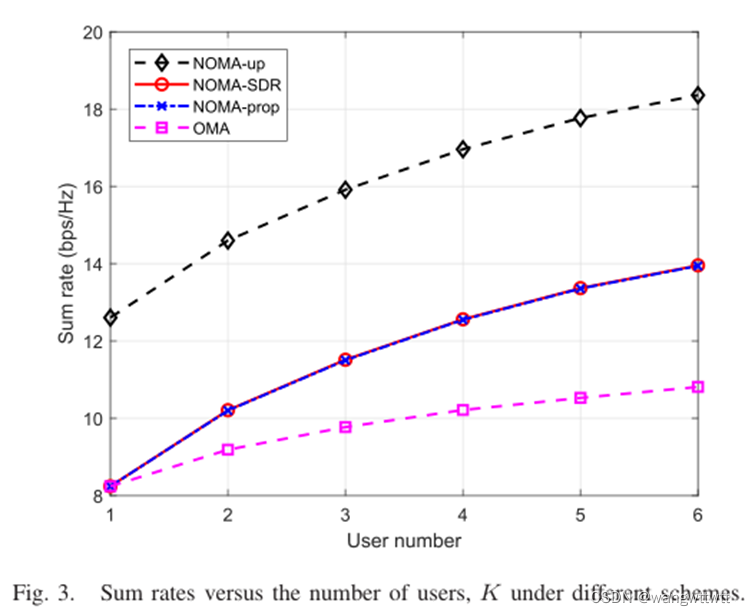
目录文章：Sum Rate Maximization for IRS-Assisted Uplink NOMA 模型传输过程优化问题（1）优化问题1 优化办法（半定松弛法）（2）优化问题2 优化办法：交替迭代算法结果分析文章：Sum Rate Maximization for IRS-Assisted Uplink NOMA 网址：Sum

社交网络影响力最大化2(Influence Maximization)

2.2 近几年研究进展及算法讲解 2.2.1 RIS(Reverse Inﬂuence Sampling) 2014年的Maximizing Social Inﬂuence in Nearly Optimal Time 2014年的Inﬂuence Maximization: Near-Optimal Time Complexity Meets Practical Efﬁciency 2015年