本文主要是介绍Sum Rate Maximization for IRS-Assisted Uplink NOMA(论文分析)(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
文章:Sum Rate Maximization for IRS-Assisted Uplink NOMA
模型
传输过程
优化问题
(1)优化问题1
优化办法(半定松弛法)
(2)优化问题2
优化办法:交替迭代算法
结果分析
文章:Sum Rate Maximization for IRS-Assisted Uplink NOMA
网址:Sum Rate Maximization for IRS-Assisted Uplink NOMA | IEEE Journals & Magazine | IEEE Xplore
模型
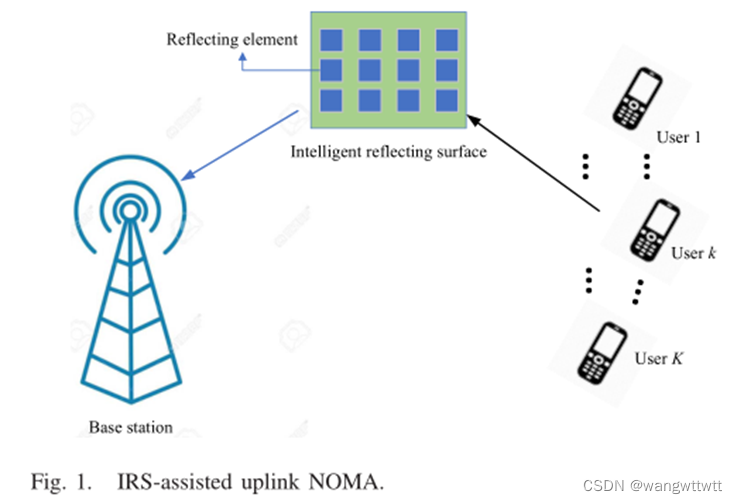
上图为IRS辅助NOMA上行链路系统,系统包含了1个基站,K个用户和由N个反射元件组成的IRS。用户和BS都配备了一个天线,假设用户和BS之间不存在直接联系, IRS在系统中作为中继,信号通过IRS反射链路到达基站,整个系统利用NOMA同时为所有用户提供服务。第k个用户发射的信号记为![]() ,其中为最大发射功率P𝑚𝑎𝑥约束下的发射功率, s为单位功率的发射信号。
,其中为最大发射功率P𝑚𝑎𝑥约束下的发射功率, s为单位功率的发射信号。
传输过程
![]() 为相位矩阵。满足
为相位矩阵。满足![]() 。假设所有信道的信道状态信息在BS和IRS完全已知。用户与RIS之间的通道用
。假设所有信道的信道状态信息在BS和IRS完全已知。用户与RIS之间的通道用![]() 表示,RIS与BS之间的通道用
表示,RIS与BS之间的通道用![]() 表示。
表示。
在BS接收到的信号可以写成:
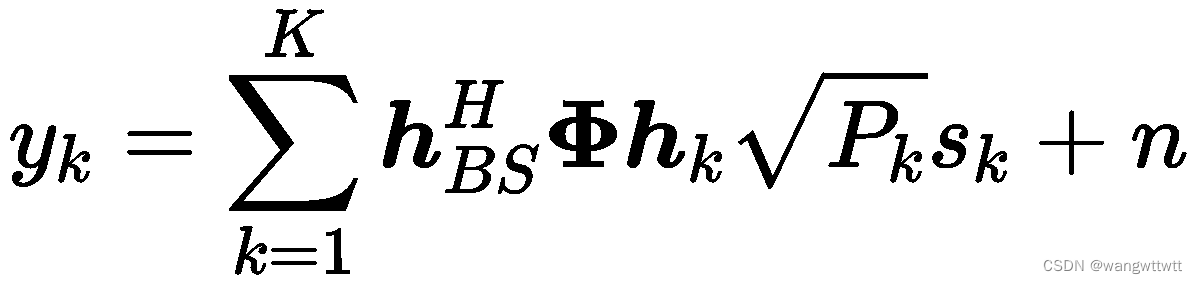
其中,n为均值为零,方差为σ^2的加性高斯白噪声。
BS使用NOMA执行连续的干扰抵消(SIC)。对于上行NOMA,信道条件较好的用户往往解码较早。假设用户按简化有效通道的降序排列,即
![]()
用户k的SINR可以表示为:
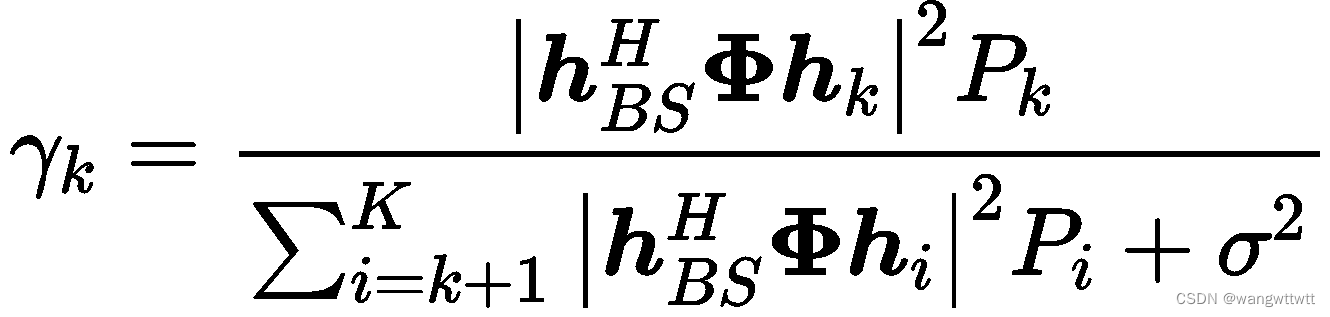
其中,当k=0时,![]() 。
。
𝑈𝑘的信息速率为:
![]()
系统的和速率为:
![]()
优化问题
(1)优化问题1
通过适当的IRS被动波束形成和用户功率控制来最大化用户的总速率。定义![]() 作为发射功率矢量。优化问题表述为:
作为发射功率矢量。优化问题表述为:
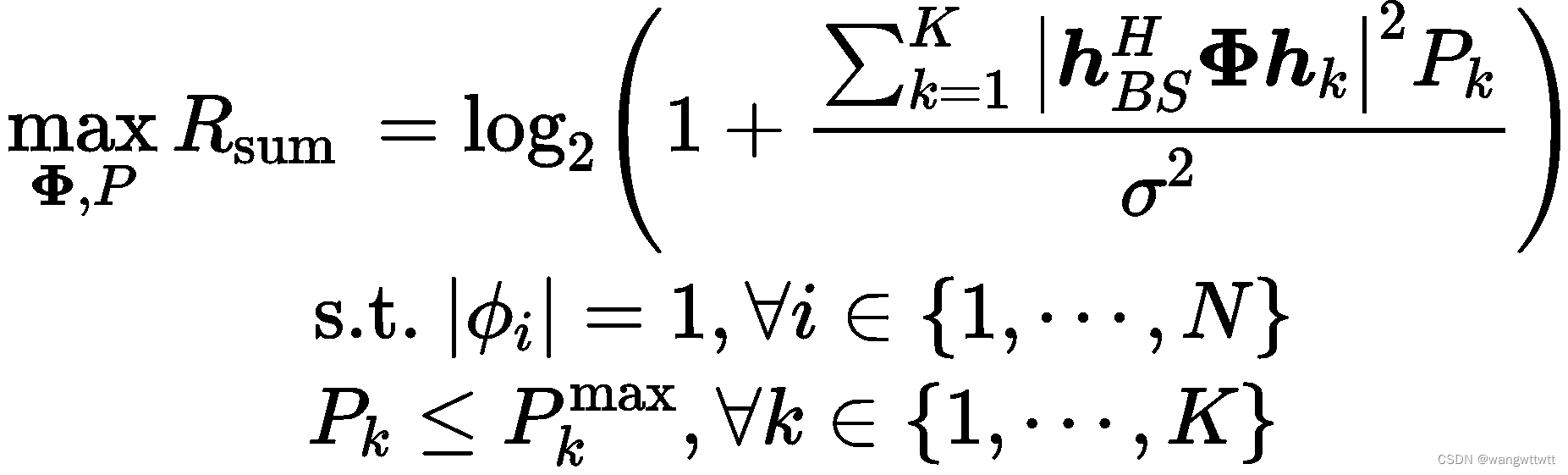
其中,![]() 为IRS相移约束,
为IRS相移约束, ![]() 为用户发射功率约束。
为用户发射功率约束。
优化办法(半定松弛法)
在相移的任意给定值下,系统的和速率随![]() 单调递增。因此,每个用户都应该以最大功率传输,以最大限度地提高和速率。
单调递增。因此,每个用户都应该以最大功率传输,以最大限度地提高和速率。
![]() 确定后,采用半定松弛法,优化IRS反射波束,可以得到近似最优解。
确定后,采用半定松弛法,优化IRS反射波束,可以得到近似最优解。
具体步骤:
为了方便计算,将对角矩阵Φ重新排列为向量![]() ,其中元素
,其中元素![]() ,引入一个辅助向量
,引入一个辅助向量![]() 。 得到,
。 得到,
![]()
和速率可以表示为:
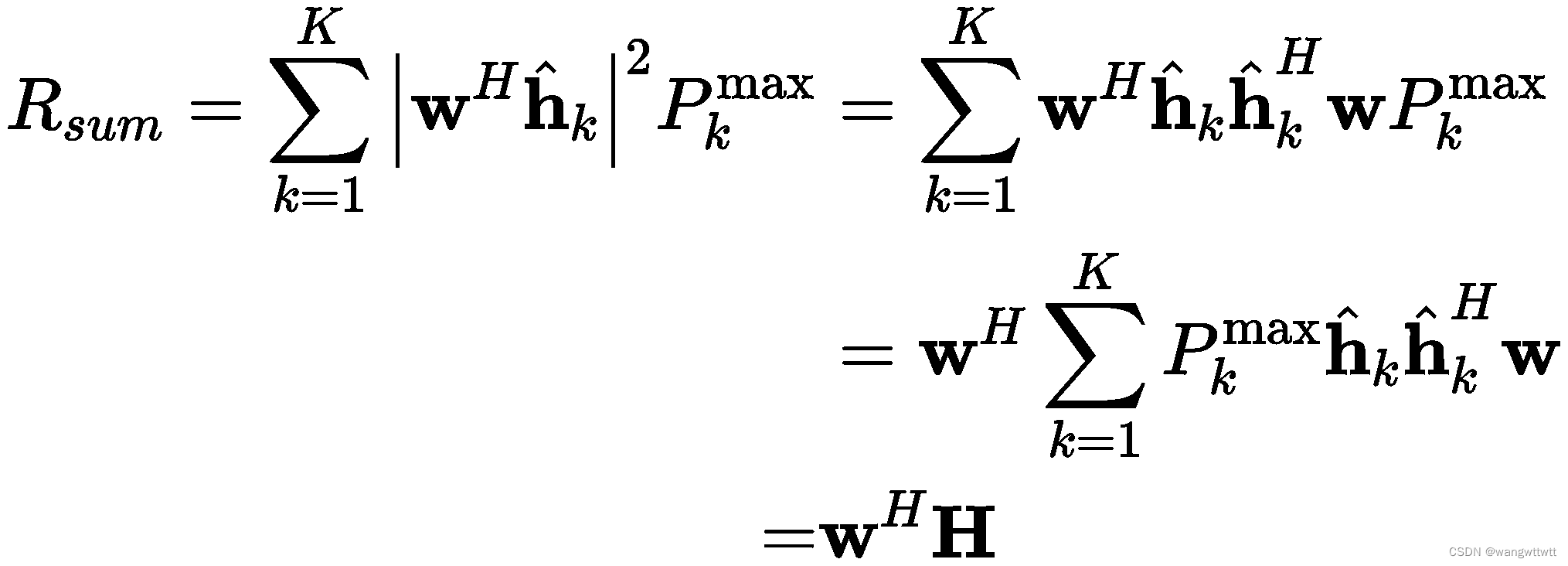
其中,![]() 。因此,优化问题可以重新表示为
。因此,优化问题可以重新表示为
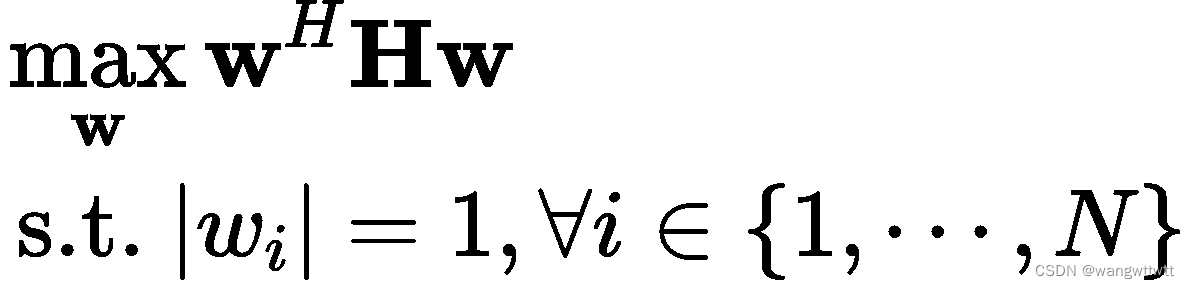
目标函数仍然是非凸的,因为我们的目标是最大化具有正半定矩阵的二次函数。同时,约束也是非凸的。根据 ![]() 。通过引入新的变量
。通过引入新的变量![]() ,可等效转化为如下问题:
,可等效转化为如下问题:
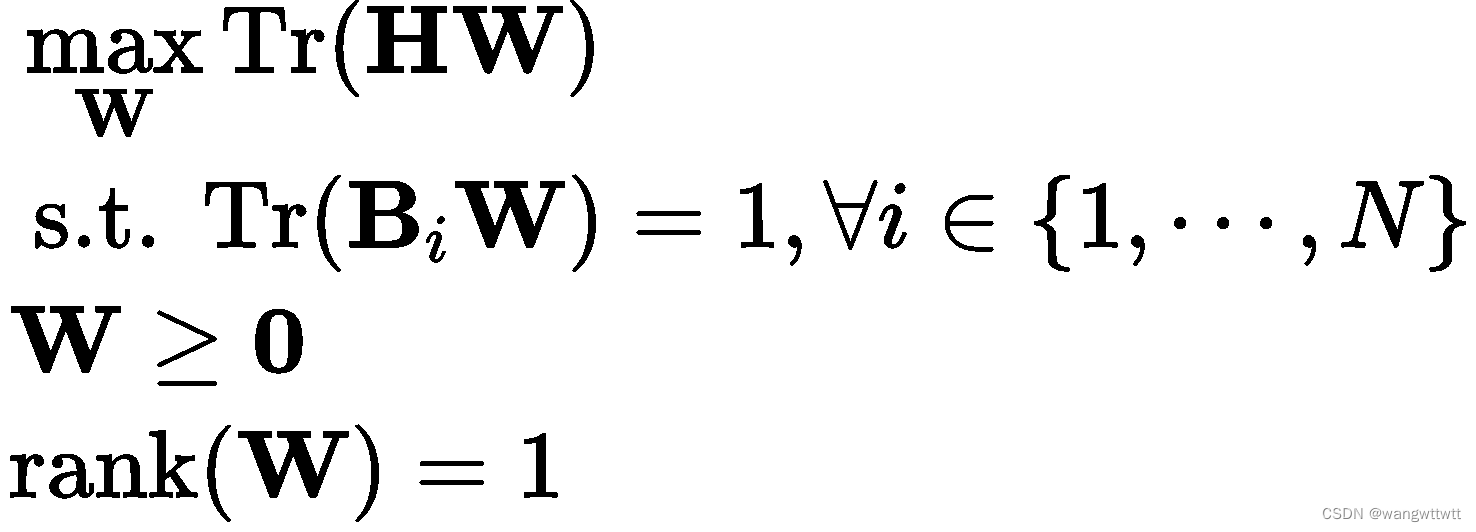
其中,由于![]() ,限制
,限制![]() 。
。![]() 只有一个非零元素,它位于
只有一个非零元素,它位于![]() , 𝐁的其余元素均为0。因此,
, 𝐁的其余元素均为0。因此,![]() 。
。
问题为半定规划,唯一的非凸约束是秩约束。工程上很自然的处理办法就是暂时忽略这个约束(松弛掉秩为1的约束),可以得到如下的简化版本:
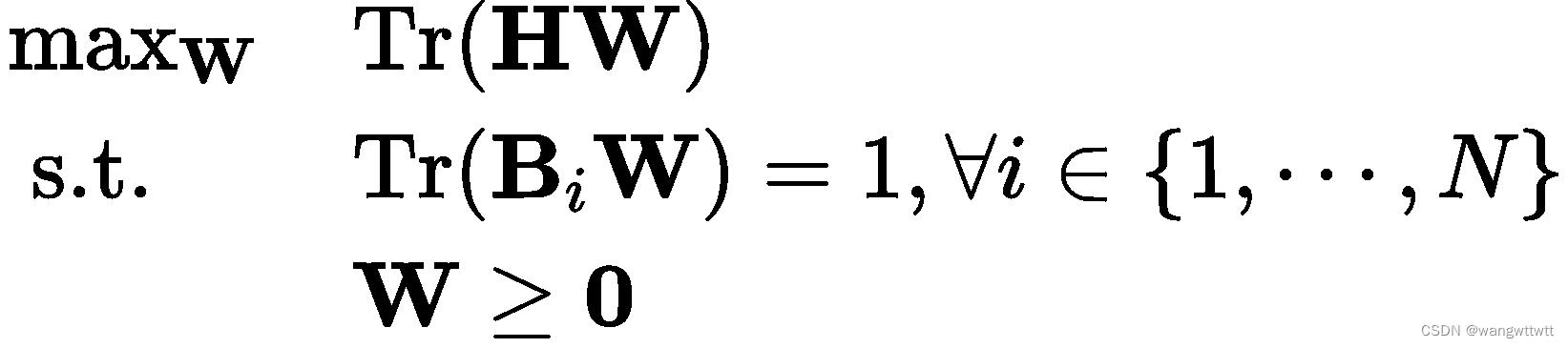
可以通过现成的软件包(如CVX)有效地解决。求解得到的最优解![]() 。
。
如果![]() 成立,那么我们可以写出
成立,那么我们可以写出![]() ,
, ![]() 将是可行且最优解。另一方面,如果秩
将是可行且最优解。另一方面,如果秩![]() ,我们需要提取一个可行的解决方案
,我们需要提取一个可行的解决方案![]() 。特征值分解(EVD)
。特征值分解(EVD)
一种最直观的想法就是, 要从![]() 中恢复𝐰,可以通过求解如下的问题:
中恢复𝐰,可以通过求解如下的问题:
![]()
闭式解就是𝐰是![]() 的最大特征向量乘以最大特征值的平方根, 即,将
的最大特征向量乘以最大特征值的平方根, 即,将![]() 的特征值分解表示为:
的特征值分解表示为:
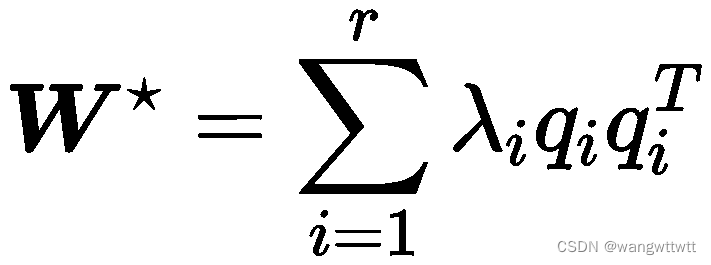
![]() 代表第i大的特征值和特征向量,那么问题的近似最优解
代表第i大的特征值和特征向量,那么问题的近似最优解![]() 。
。
(2)优化问题2
上述优化问题1,不能保证每个用户的服务质量(QoS)。为了克服这个问题,我们假设每个用户都有一个必须满足的最低速率要求。优化问题表述为:
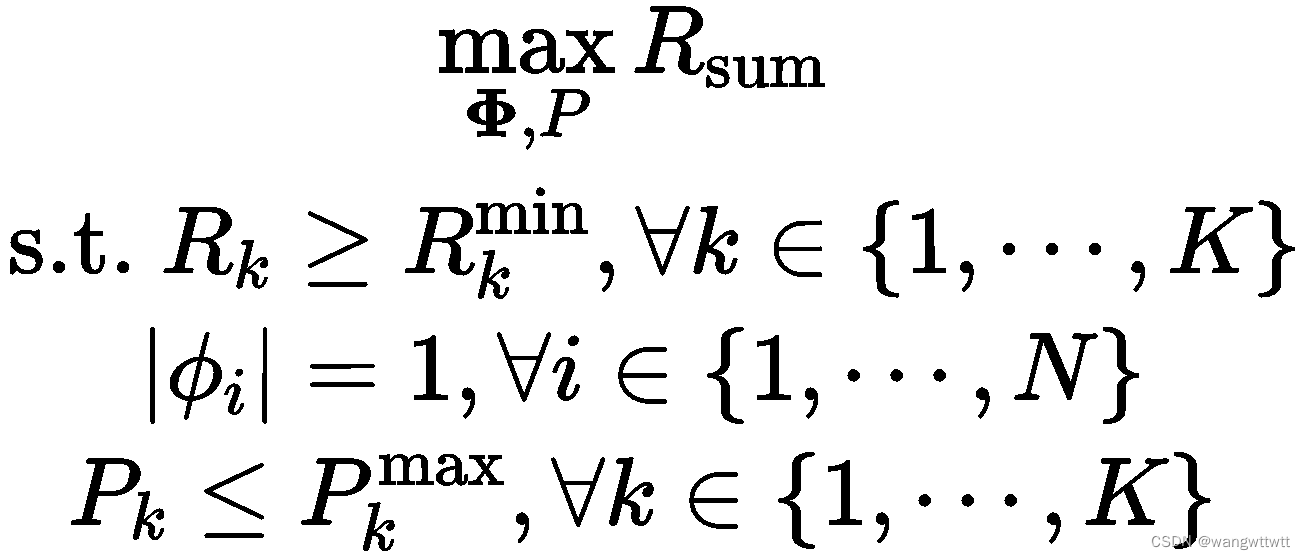
优化办法:交替迭代算法
a.功率分配:在给定Φ值下,功率分配问题表示为
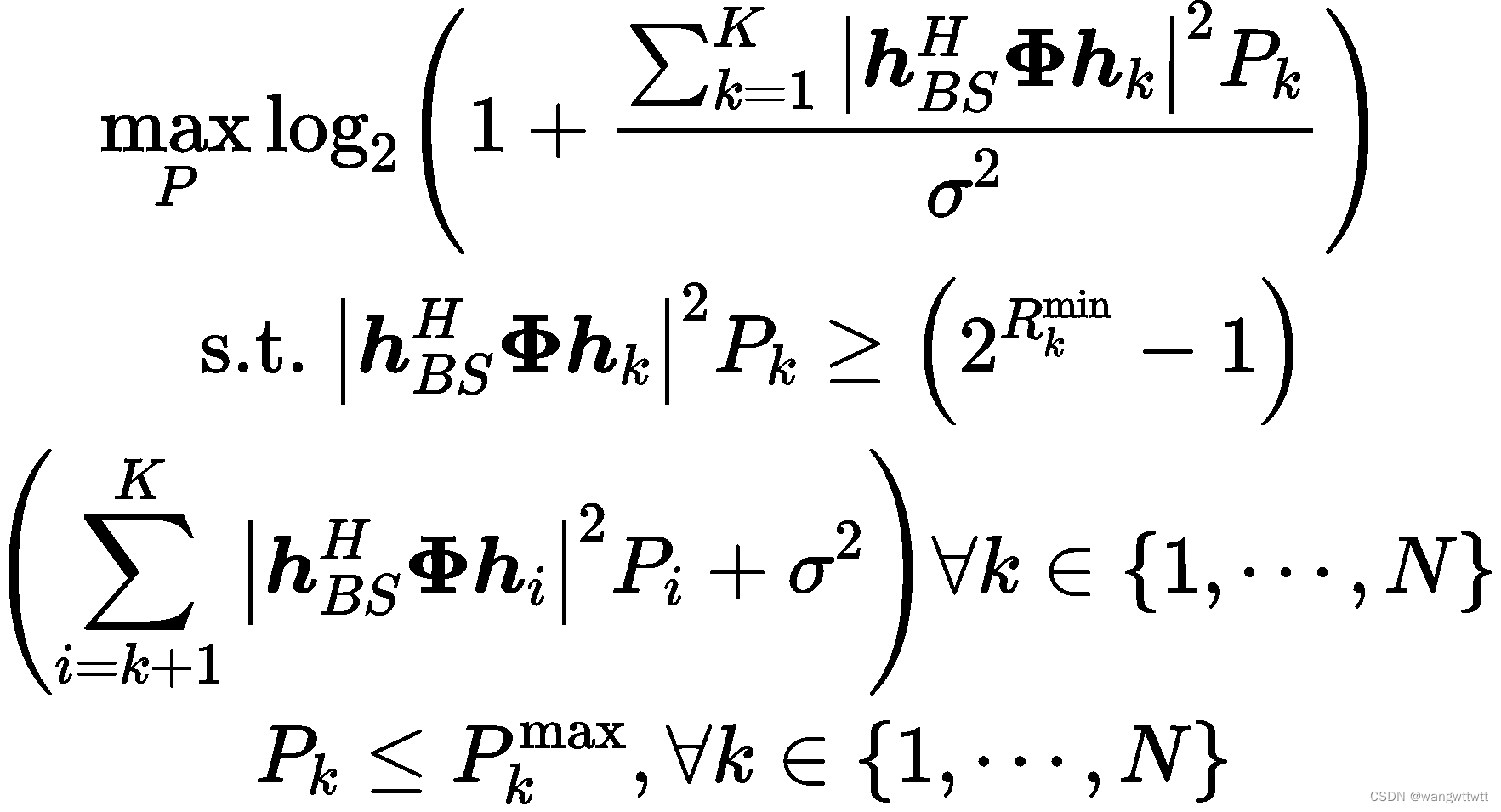
凸优化问题,可以使用凸优化工具(CVX),如内点法。
b.IRS波束形成:在给定P值下,采用半定松弛法,得到近似最优解。
与上面步骤的类似,问题可以重新表示为
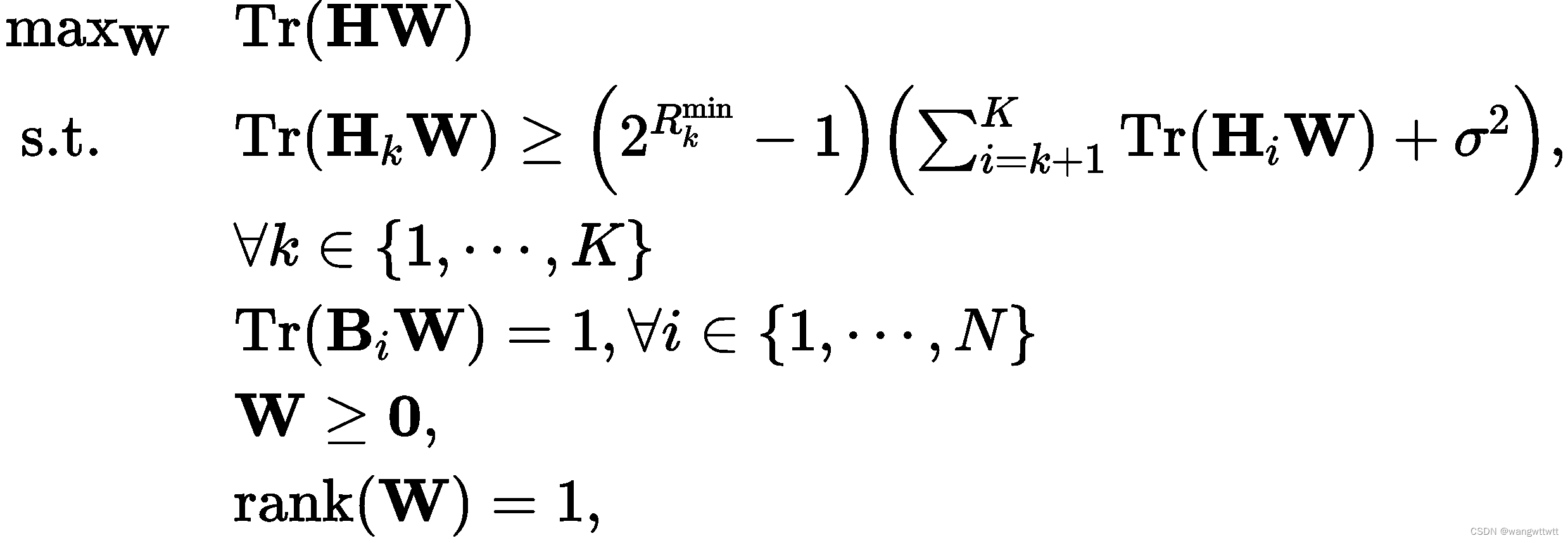
其中, ![]() 。
。
c.迭代更新直到收敛:重复功率分配和IRS波束形成优化,直到收敛。
结果分析
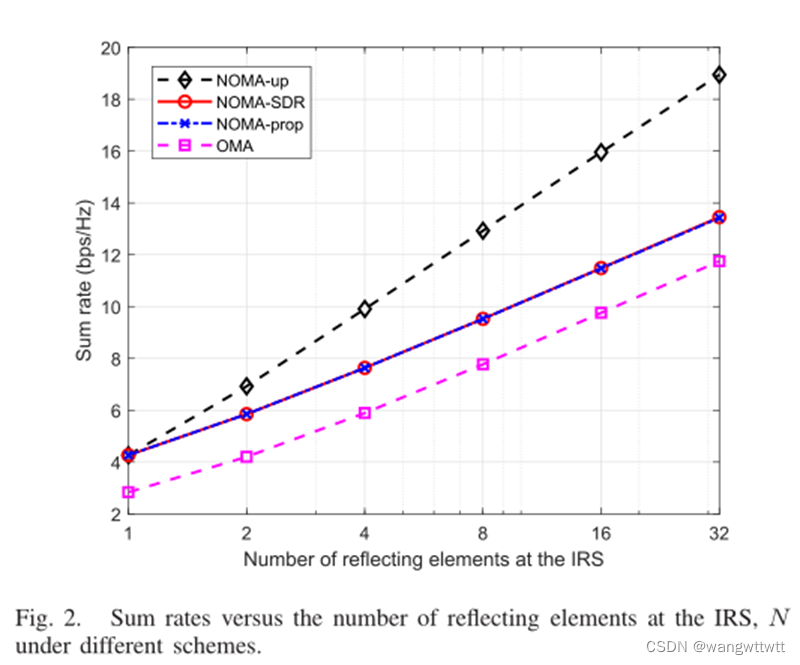
通过比较三种NOMA方案,(1)NOMA- SDR提供了比NOMA-up更严格的上界。
(2)NOMA-SDR和NOMA-prop的表现接近,表明NOMA-prop接近最优,由于NOMA-prop 增加对每个用户信噪比约束。
(3)验证了NOMA优于OMA,是由于NOMA 技术可以使不同的用户在时间域和频率域上复用资源带来的。
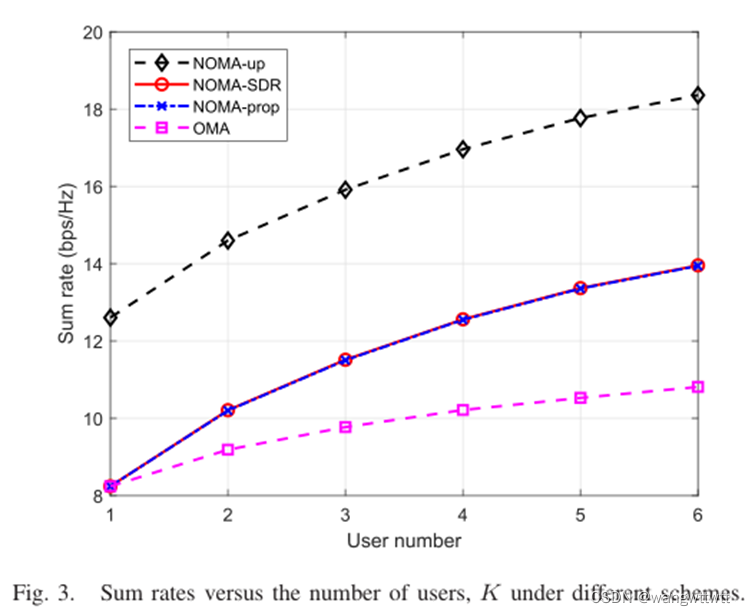
图3显示了总速率与用户数量的关系。
当K > 1时,NOMA-prop在和率方面优于OMA,且差距随着K的增大而增大,这是因为在NOMA中,由于IRS同时为所有用户提供服务,因此有复用增益可用。相比之下,OMA只能获得功率增益,因为用户是使用正交资源服务的。
这篇关于Sum Rate Maximization for IRS-Assisted Uplink NOMA(论文分析)(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




