本文主要是介绍EM算法(expectation maximization algorithms)揭秘,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
EM算法篇
EM算法简介
EM算法,也叫expectation maximization algorithms,是在包含隐变量(未观察到的潜在变量)的概率模型中寻找参数最大似然估计(也叫最大后验估计)的迭代算法。EM 算法在期望 (E步骤) 和最大化 (M步骤) 之间交替执行,前者计算模型参数当前估计的对数似然期望函数,后者对E步骤中找到的预期对数似然计算最大化,然后使用参数新估计值来确定下一个E步骤中隐变量的分布。EM算法是很多机器学习算法的基础,如GMM、HMM、GAN、FA等。
EM算法核心
令所有可观测变量为X,所有隐变量为Z,以及为模型参数,那么
表示被
支配的X和Z联合概率分布。我们的目标是最大化似然函数
。
1. 选择初始模型参数
2. E步骤:计算
3. M步骤:利用公式,计算
,
其中
4. 判断目标对数似然函数(即)和模型参数
是否收敛,有一个收敛即可,如果都不满足,那么令
,并返回第2步。否则结束算法。
思考:上述步骤的如何与目标对数似然函数
建立联系?见推导部分
背景知识:KL散度
KL散度(全称是 Kullback-Leibler 散度,也称为相对熵和I 散度),表示为,是一种统计距离,它衡量两个概率分布(P和Q)的差异程度(因此是非负的)。一个简单解释是,当实际分布为P时,使用Q作为预期时的额外惊喜。它的重要性质是不对称,或说不符合交换律,一般来说
。另外,它也不满足三角不等式。相对熵为 0 表示两个分布具有相同的信息量。从Q到P的相对熵
公式一般表示为:
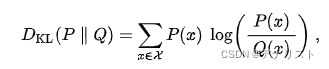
其等价于

也就是说,它是概率分布P和Q之间的对数差的期望,其中使用前概率P获取该期望。
KL散度(相对熵)和交叉熵的关系
P和Q的KL散度(相对熵)等于P和Q的交叉熵减去P的熵(即P 与自身的交叉熵),具体推导如下
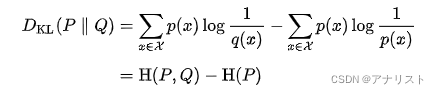
EM推导过程
首先,我们对进行改写,引入隐变量Z的求和,显然有:
=
(0)
这里我们假设X和Z都是离散的变量,当处理连续变量时,只需要把求和()变为积分(
)即可。
我们注意到,直接优化是困难的,但是优化
是相对容易的。我们把X和Z的组合叫做完全数据(complete-data )。我们定义一个函数
表示隐变量Z的分布。我们发现对于任意的
,有如下等式成立:
(1)
其中 (2)
以及 (3)
思考:怎么验证?很简单,公式(2)和(3)相加,首先提取,由于
是Z的分布,所以求和为1。然后两个ln对数相加,即
,而
,因此等号成立。
注意:这里的是q和
的函数,而q本身又是Z的函数。另外,
包含X和Z的联合概率;
包含已知X求Z的条件概率。当然,
有个负号。
是
和
的KL散度。因此
>=0,当且仅当
=
时,等号成立。因此,根据公式(1)有:
,换言之,
是
的一个下界。因此,我们可以作图如下:
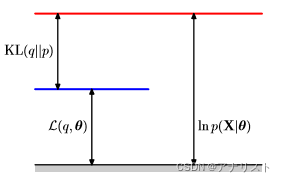 (左边两根黑色竖线的高度之和等于右边竖线的高度)
(左边两根黑色竖线的高度之和等于右边竖线的高度)
再次强调,以上公式和图对任意都成立。
EM算法是利用两阶段迭代优化来找到最大似然解的算法。可以利用公式(1)来定义EM算法,并证明它确实能够最大化log likelihood,即。假设当前参数向量是
,在E步骤中,对下界
关于q(即
)进行最大化,其中保持
固定。注意到,
不依赖于q(即
),因此
的最大值只会发生在KL散度消失的时候,即
=0。这意味着q=p,即
=
,此时下界等于所求的log likelihood,如下图所示:
 (注意,此时两根黑色竖线一样高)
(注意,此时两根黑色竖线一样高)
在接下来的M步骤中,保持固定,让下界
关于
最大化,得到新的
值,叫做
,这样会造成下界
变大,除非已经到达最大值点。而下界的增加就会推动 log likelihood(即
)的增加。由于
是利用
而非
得到的,且在M步骤中保持固定,它自然不会等于
,因此一定会存在一个非零的KL散度。这意味着,log likelihood的增加幅度会大于下界的增加,如下图所示:
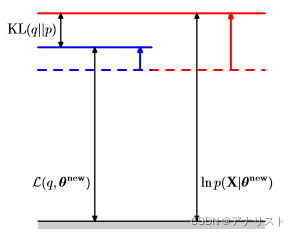 (M步骤中出现非零的KL散度;同时log likelihood的增加幅度(红线所示)大于下界的增加幅度(蓝色所示))
(M步骤中出现非零的KL散度;同时log likelihood的增加幅度(红线所示)大于下界的增加幅度(蓝色所示))
如果我们替换公式(2)中的为
,即根据
=0,那么在E步骤之后,下界就变为:
把上式记为,其中
代表右项,表示常量,这里是
(即
)的负熵,它独立于
。(这里的
展开和上面EM算法的M步骤一致!)
注意到只在ln中出现,即
,如果
包含指数形式或指数乘积形式,那么对数ln就能和指数一起抵消,最终导致在M步骤中,完全数据(complete-data )的求对数似然函数的极大值,即
,比不完全数据(incomplete-data )的求对数似然函数的极大值,即
,更简化。
EM算法的运算过程随着的更新可表示如下图:
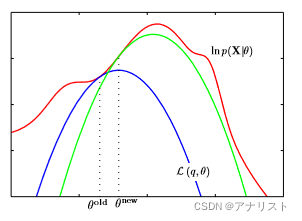 (当模型参数
(当模型参数从
变为
,下界
推动log likelihood(即
)变化;最大化下界得到新的
;不断迭代)
为了最大化红色曲线代表的不完全数据(incomplete-data )的对数似然函数,即,从初始的
开始,在第一轮E步骤中,首先评估潜在变量的后验分布,这产生一个下界如
,如图蓝色曲线在
的取值,其实就是蓝色和红色的切点,意味着此刻两条曲线有相同的梯度。而蓝色曲线(即下界)是一个凸函数(对于指数族及其混合形式来说,这里指
),只有一个极大点。在M步骤中,对下界最大化得到
,从而相对于
,把log likelihood(即
)往大的方向推动。在第二轮的E步骤又构造新的下界(绿色曲线),与红色曲线正切于
。这就是EM算法的形象化运行轨迹。
EM应用篇(GMM)
背景知识:高斯分布
高斯分布(Gaussian distribution)也叫正态分布(normal distribution),是一种广泛使用的连续变量概率分布,对于单变量x来说,其概率密度函数为:
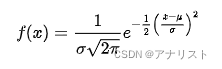 (公式Ⅰ-0)
(公式Ⅰ-0)
这里做简单的变形,且用代替f(x),表示为:
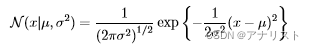 (公式Ⅰ-1)
(公式Ⅰ-1)
其中µ 、σ 分别表示均值和标准差。对于一个D维的向量X来说,多变量高斯分布可表达为:
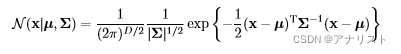 (公式Ⅰ-2)
(公式Ⅰ-2)
其中µ 表示均值向量,Σ 表示DxD维的协方差矩阵。而|Σ|表示Σ 的行列式的值。
GMM基本介绍
高斯混合模型,是多个含有离散隐变量的高斯分布,可以写为高斯模型的线性叠加形式,如下
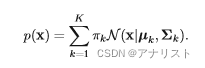 (公式 Ⅱ)
(公式 Ⅱ)
K表示高斯模型的个数;令z是K维的随机变量向量,其值只能取0或1(即{0, 1}),且只有一个
值为1,其余都是0;因此有
;此时可以定义联合分布
,我们称
是z的边缘概率分布,
是已知z求x的条件分布。
现在思考和模型混合参数
的关系,很明显,
,其中
满足:
,以及
的总和为1,即:
(公式 Ⅲ)
此时是一个有效的概率变量。由于
是只有1个1元素的K维向量(其余都为0),因此
可改写为
(公式 Ⅳ)
类似的,已知某个为1(此时其余z元素全为0)求x的条件概率可直接表示为:
上式是结合公式 Ⅱ和公式 Ⅳ得到的。现在把元素扩展到整个z向量,就有:
(公式 Ⅴ)
注意上式对所有k,只有一个=1,其余为0,因此得以成立。
根据贝叶斯公式得到联合概率,另外有
,因此
将公式Ⅳ和公式Ⅴ代入上式,并将z向量展开为多个元素的形式,同时注意只有一个
=1,其余为0的事实,得到:
(公式 Ⅵ)
这样我们就推导出了的表达式,发现没,公式 Ⅵ和公式 Ⅱ完全等价!
公式 Ⅵ蕴含着这样一个事实,任何一个观测数据的背后对应了一个隐变量
!
现在我们能够用联合概率分布代替
来解决GMM问题,这样就能用EM算法来简化。
现在考虑已知x求某个=1的条件概率
,这个变量含义是,当观测到变量x时,
=1的后验概率,它可以看成混合高斯的某个高斯成分对解释x变量所起到的某种“责任”,或说负责解释的比例。记
,那么根据贝叶斯规则,即
,得到
 (公式 Ⅶ)
(公式 Ⅶ)
别忘记,,表示
的先验概率。因此
表示当观测到变量x时,
的后验概率。
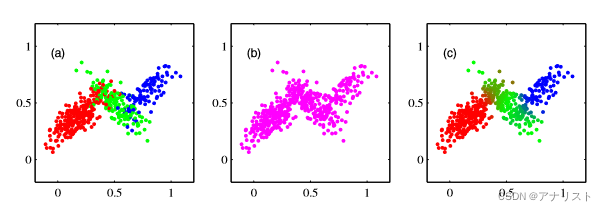
上图a为三个高斯500个点的可视化图,分别用红绿蓝表示,可以理解为联合分布,其中z的状态有3种,因为不仅能区分出3堆(高斯个数),而且还能确定哪个数据点属于哪一堆;上图b表示边际分布
,我们只能大概看出有3堆,但不能确定哪个点属于哪个堆,它没有包含z的信息。上图a叫做完全数据(complete-data ),上图b叫做不完全数据(incomplete-data )。上图c表示每个数据点和每个高斯成分之间的关联
,即某个数据点有多大概率来自某个高斯,举个例子,如果
,那么整个点会涂成红色,如果
,那么会涂相同比例的绿色和蓝色,于是得到藏青色。显然,上图a和c的区别是,一个是“硬分类”,一个是“软分类”。
GMM求最大似然
假设有观测数据{,
,..,
},我们想用GMM建模它,我们可以用NxD的矩阵
来表示,其中第n行表示为
。类似的,隐变量Z是NxK的矩阵,其中第n行为
。
现在对公式Ⅱ取对数似然,得到:
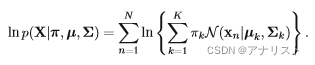 (公式 Ⅷ)
(公式 Ⅷ)
其中是矩阵,而不是单个变量,因此右边需要对所有点求和,即加上
;至于如何最大化这个函数,首先要讨论一下GMM的奇点问题。考虑一个GMM,其协方差矩阵为
,其中
是单位矩阵(最后的结论对其他协方差矩阵也一样,这里为了简化讨论)。假设其中一个高斯分布(比如第j个),它的均值
刚好等于其中一个数据点
,即
,那么这个点的概率可以写为(代入公式Ⅰ-1):
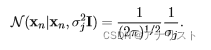
当考虑σj → 0时,这一变量是无穷大,其对数似然也是无穷大。因此对它求最大值不是一个定义良好的问题。这就是奇点问题,只要GMM有一个高斯成分坍塌到一个特定点,那么总会存在奇点问题。思考:为啥单高斯分布不存在奇点问题?
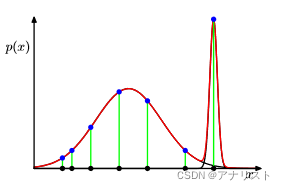 (GMM的奇点问题)
(GMM的奇点问题)
GMM存在的奇点,在最大似然求值中,会导致严重的过拟合,而只要我们用贝叶斯方法就能克服这个问题。再次强调,我们需要避免找到这种病理(或病态)的解决方案,而至少要找到局部最优解,当然全局最优解更好。一个启发式方法是,当我们发现一个高斯成分要坍塌的时候,可以随机初始化它的均值,同时把它的协方差设置成比较大的值,然后继续最优化。
另一个最大似然问题存在的事项是,假如有K个高斯成分,对于给定的最大似然解,就一共有个等价的解,因为有
种方式将K个参数组合赋值给K个高斯成分。因此对于特定的参数空间的解,总存在另外
个解代表相同的分布。这个叫做GMM的可识别性(identifiability )问题。理解这个问题,有助于我们理解GMM。但在本文中,我们认为等价的各个解是一样好的,不去做区分。
对于GMM(公式Ⅷ)的对数似然最大化比单个高斯要复杂,因为ln对数中存在对k的求和,因此ln就无法直接作用在高斯上。直接令该式的导数等于0,将无法得到闭合形式的解。一个解决方案是利用基于梯度的方法(如梯度下降法),但本文还是继续介绍EM算法的能力,毕竟EM的应用是非常广的,其中就包括GMM场景。
GMM中引入EM
现在正式讨论如何用EM解决GMM的优化问题。令公式Ⅷ的对均值
求偏导并令其为0,我们得到:
 (公式 Ⅸ)
(公式 Ⅸ)
这里的高斯分布采用公式Ⅰ-2形式。此时发现等式右侧的中天然存在
,表示每个数据点和每个高斯成分之间的关联。假设协方差矩阵
非奇异,那么两边乘以
并重新整理,得到:
(公式 Ⅹ)
其中定义为:
(公式 Ⅺ)
感官上可理解为落在第k个高斯分布上的数据点数。而公式 Ⅹ可理解为第k个高斯成分的均值是各个数据点的加权平均得到的,而权重因子正是
,表示某个高斯成分有多大概率生成了该数据点。
现在令公式Ⅷ的对协方差
求偏导并令其为0,我们得到:
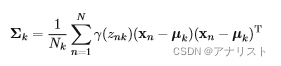 (公式 Ⅻ)
(公式 Ⅻ)
同样可看成是各个数据点的一种加权平均,权重因子也是。
最后考虑公式Ⅷ的对混合系数
求偏导,并最大化。此时要考虑
的约束,即公式 Ⅲ,也就是
对所有k的求和必须为1. 利用拉格朗日乘子法,构造出以下待最大化的目标方程:
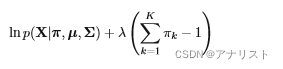 (公式 XIII)
(公式 XIII)
现在令公式XIII对混合系数求偏导并令其为0,我们得到:
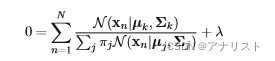 (公式 XIV)
(公式 XIV)
此时我们似乎又看到了的影子,现在我们对等式两边同乘以
,并利用公式Ⅲ,即
对k从1到K求和为1,给等式两边对k求和(加上
),我们进一步得到:
(公式 XV)
因此有 (公式 XVI )
把公式XVI代入公式XV,整理得到:
结合公式Ⅺ,得到:
(公式 XVII )
可见,GMM的某个高斯成分的混合系数是由落到该高斯上的数据点数占所有点数的比例。
现在回头看的表达式,即公式Ⅶ,发现
以一种复杂的方式依赖
、
、
三个模型参数,因此可能并不存在闭合形式的解。不过结合公式X、公式XII、公式XVII可发现,两者存在一种简单的迭代模式,可用来寻找最大似然的解。这就是使用EM算法的动机。
EM算法中,首先初始化模型参数,然后在E步中计算,然后在M步中重新计算模型参数。注意,要先计算均值,再计算协方差。我们会发现,从E步到M步的每次更新,都能保证增加目标对数似然函数的值。
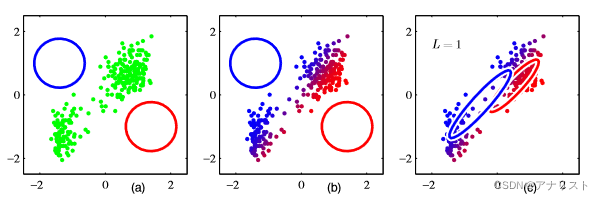
上图是两个高斯成分GMM的EM过程,图a中绿色是数据点,蓝色和红色是标准差等值线。图b表示第一次E步后,其中蓝色表示一些数据点被认为是来自蓝色的高斯成分,红色与之类似,而紫色(重合点)表示一些点被同时认为来自两个高斯分布的概率都比较高。图c表示第一次M步后,两色的均值和标准差都往数据集的中心移动。
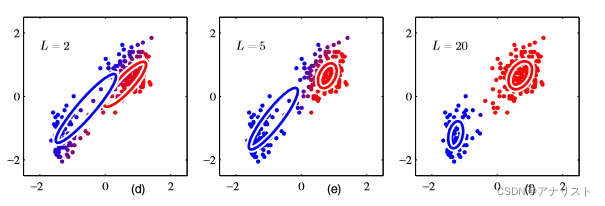
以上三图(d/e/f)分别表示经过2、5、20轮EM迭代后的情况。其中图f接近于收敛。
比起k-means算法,EM一般需要迭代更多次数来到达收敛,每一轮的计算量也更大。因此有必要用k-means辅助初始化,帮助找到比较好的初始值。需要强调,EM并不保证找到全局最优解,初始值对此有影响。存在多种启发式或元启发式方法来避开局部最大值,例如随机重新启动爬山(从几个不同的随机初始估计开始),或应用模拟退火方法。
基于EM的GMM完整算法
已知高斯混合模型,我们的目标是最大化似然函数,其中变量是模型参数(均值、协方差、混合系数),分别用、
、
表示。
1. 初始化所有模型参数,并计算一遍目标函数的值
2. E步骤:利用已知模型参数,计算:

3. M步骤:利用新的重新评估模型参数,即:

其中
4. 计算目标对数似然函数的值,即
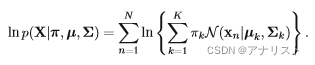
并检查模型参数和对数似然函数是否收敛,如果不满足,回到第2步。否则结束算法。
参考资料
EM算法,维基百科。
混合模型,维基百科。
《模式识别与机器学习》,2006 年。
这篇关于EM算法(expectation maximization algorithms)揭秘的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








