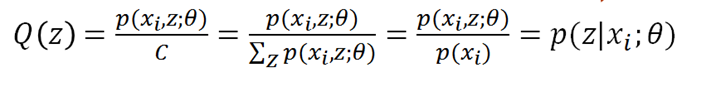em专题
高斯混合模型(GMM)的EM算法实现
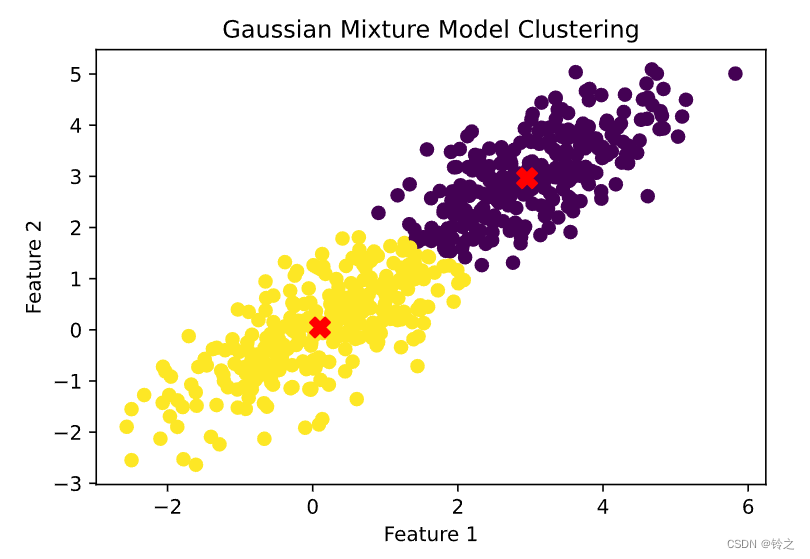
在 聚类算法K-Means, K-Medoids, GMM, Spectral clustering,Ncut一文中我们给出了GMM算法的基本模型与似然函数,在EM算法原理中对EM算法的实现与收敛性证明进行了详细说明。本文主要针对如何用EM算法在混合高斯模型下进行聚类进行代码上的分析说明。 GMM模型: 每个 GMM 由 K 个 Gaussian 分布组成,每个 Gaussian 称为一个“C
前端面试:title与h1的区别、b与strong的区别、i与em的区别?
在前端开发中,理解 HTML 标签的区别和语义非常重要,以便更好地组织内容和优化搜索引擎优化(SEO)。以下是 title 与 h1、b 与 strong、i 与 em 的区别: 1. title 与 h1 title: 位置:位于 <head> 标签中。目的:定义文档的标题,通常在浏览器标签页显示,搜索引擎结果页面中也使用该标题。语义:表示文档的主题。示例: <head> <title
POJ 2993Emag eht htiw Em Pleh(模拟)
题目地址:http://poj.org/problem?id=2993 这个题以前做过一遍。。当时居然没写博客。。这题其实也算不上模拟吧,我只是用了几套公式。。 #include <stdio.h>#include <string.h>char map[50][50];int main(){char s1[200], s2[200];int i, j, len1, len2, x,
B,strong,I,em的区别
很多网页编写者不明白b和strong以及i和em具体含义,写文章的时候只是用网站后台的编辑器排版文章,需要加粗的时候点击编辑器上面的B按钮就行了。因为两者所达到的效果一样,所以人们就没有太在意这两个到底有什么区别,那么今天我来告诉大家,是有区别的。 它们的区别就再于一个是物理元素,一个是逻辑元素。 什么是物理元素?什么是逻辑元素? 物理元素所强调的是一种物理行为,比如说我把一段文字用b标记
GMM与EM算法(一)
EM是我一直想深入学习的算法之一,第一次听说是在NLP课中的HMM那一节,为了解决HMM的参数估计问题,使用了EM算法。在之后的MT中的词对齐中也用到了。在Mitchell的书中也提到EM可以用于贝叶斯网络中。 下面主要介绍EM的整个推导过程。 1. Jensen不等式 回顾优化理论中的一些概念。设f是定义域为实数的函数,如果对于所有的实数x,,那么f是凸函数。当x是向量
第9章 EM算法:例题及课后习题
1 概要 1.EM算法是含有隐变量的概率模型极大似然估计或极大后验概率估计的迭代算法。含有隐变量的概率模型的数据表示为 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ)。这里, Y Y Y是观测变量的数据, Z Z Z是隐变量的数据, θ \theta θ 是模型参数。EM算法通过迭代求解观测数据的对数似然函数 L ( θ ) = log P ( Y ∣ θ )
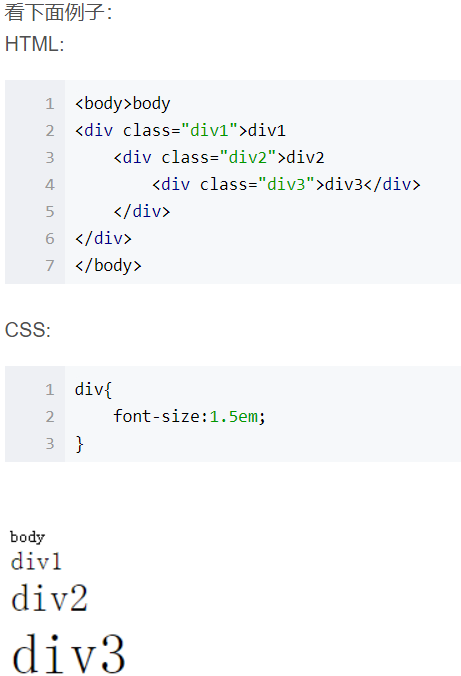
em、rem、px区别
css中如何区分em、rem、px? 随着css学习的不断深入页面也随之丰富,那么em、rem、px是我们在页面布局中经常会用到的单位,也是面试题中老生常谈的一个问题,经久不衰,那我们今天用我们的小案例来解释他们的区别吧! px(像素) px这个单位用的非常多,我们大多数人都很熟悉了吧。px单位的名称为像素,它是一个固定大小的单元,像素的计算是针对(电脑/手机)屏幕的,一个像素(1px)就是
ADS基础教程21 - 电磁仿真(EM)模型的远场和场可视化
模型的远场和场可视化 一、引言二、操作步骤1.定义参数2.执行远场视图(失败案例)3.重新仿真提取参数 三、总结 一、引言 本文介绍电磁仿真模型的远场和场可视化。 二、操作步骤 1.定义参数 1)在Layout视图,工具栏中点击EM调出模型设置界面。 2)在模型设置界面中,首先设置Output Plan,将Save current for:选择All generate
极客战记砸死他们全家(bash ‘em all) 通关代码
这一关没有难度,面对经过训练的食人魔暴力杀死他们需要很好的装备,然而杀死他们后我们也不能够很好的通过雷区,因此采用盾牌的bash技能击退他们让他们帮我们探雷。想要完美通关需要注意以下几点: 务必在击退食人魔后回到初始位置等待,因为食人魔击退后到雷区需要一定的时间,如果不等待,英雄会踩雷阵亡在拾取宝石后,应再次返回初始位置,否则英雄会被地形卡住造成超时无法完成任务。两次回到初始位置也是为了等待ba
ADS基础教程20 - 电磁仿真(EM)参数化
EM介绍 一、引言二、参数化设置1.参数定义2.参数赋值3.创建EM模型和符号 四、总结 一、引言 参数化EM仿真,是在Layout环境下创建参数,相当于在原理图中声明变量。 二、参数化设置 1.参数定义 1)在Layout视图,菜单栏中选中EM>Component>Parameters… 2)在弹出的参数编辑框中,Create/Edit Parameter有一栏Ty
【机器学习算法】期望最大化(EM)算法概述
期望最大化(EM)算法是一种迭代算法,用于在有未观测变量的情况下,求解概率模型参数的最大似然估计或最大后验估计。以下是对EM算法的原理与应用进行详细地剖析: EM算法原理 E步 - 期望计算:根据当前估计的模型参数,计算隐变量的期望值[1]。这个步骤利用了已知的观测数据和当前的参数估计,来更新隐变量的概率分布。M步 - 最大化:基于E步计算得到的隐变量期望,更新模型参数以最大化似然函数[1]。这
【机器学习】高斯混合模型GMM和EM算法
百度百科:高斯混合模型就是用高斯概率密度函数(正态分布曲线)精确地量化事物,它是一个将事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。 高斯混合模型(GMM),顾名思义,就是数据可以看作是从数个单高斯分布(GSM)中生成出来的。虽然我们可以用不同的分布来随意地构造 XX Mixture Model ,但是 GMM最为流行。另外,Mixture
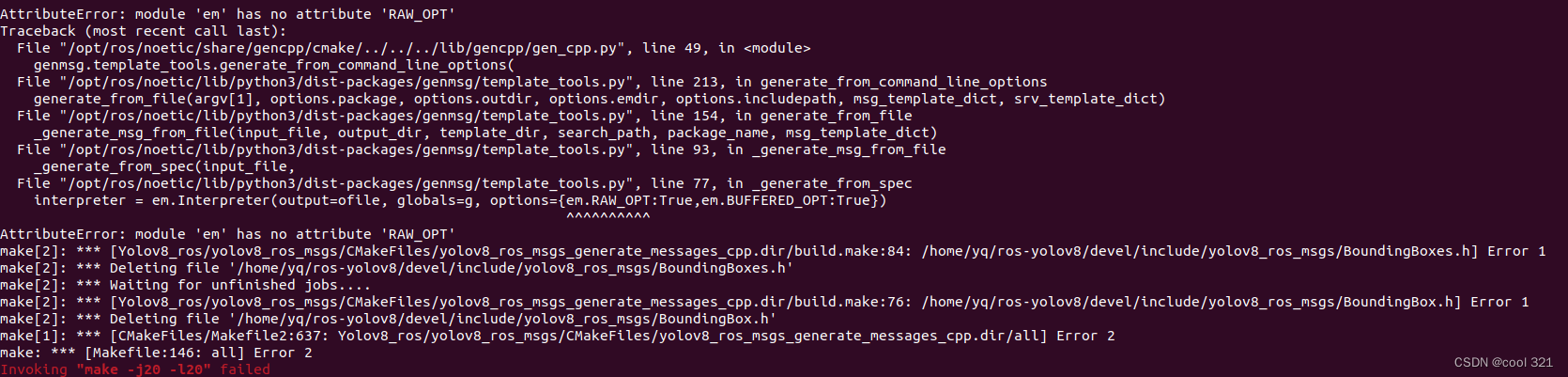
AttributeError: module ‘em‘ has no attribute ‘RAW_OPT‘
解决方案: pip uninstall empypip install empy==3.3.2
数字图像处理成长之路15:前景提取(最大似然估计EM算法与高斯混合模型)
先实践一下何为前景提取: 原始图像 如果画面中有移动的物体,会以白色表现出来。 我理解的前景提取就是把画面中移动的物体提取出来。 这是opencv中给的示意图,来简单看看opencv代码: - 代码 // Global variablesMat frame; //current frameMat fgMaskMOG2; //fg mask fg mask gener
数据挖掘算法之 EM 算法(高斯混合修正)
一、什么是EM算法? EM(期望最大化)算法是一种被广泛用于极大似然估计(ML)的迭代型的计算方法,对处理大量的数据不完整问题非常有用,简化有限混合模型ML拟合问题的处理,经常用在机器学习和数据聚类中。 二、EM算法思想: EM算法主要分为期望步骤(E-step)和最大化步骤(M-step),以高斯混合修正为例: E-step:
【机器学习】期望最大化(EM)算法
文章目录 一、极大似然估计1.1 基本原理1.2 举例说明 二、Jensen不等式三、EM算法3.1 隐变量 与 观测变量3.2 为什么要用EM3.3 引入Jensen不等式3.4 EM算法步骤3.5 EM算法总结 参考资料 EM是一种解决 存在隐含变量优化问题 的有效方法。EM的意思是“期望最大化(Expectation Maximization)” 。EM是解决(不完全数据,含
sheng的学习笔记-AI-EM算法
AI学习笔记目录:sheng的学习笔记-AI目录-CSDN博客 目录 基础知识 什么是EM算法 EM算法简介 数学知识 极大似然估计 问题描述 用数学知识解决现实问题 最大似然函数估计值的求解步骤 Jensen不等式 定义 EM算法详解 问题描述 EM算法推导流程 EM算法流程 小结 EM算法实例 基础知识 什么是EM算法 EM(Expectat
统计计算二|EM算法(Expectation-Maximization Algorithm,期望最大化算法)
系列文章目录 统计计算一|非线性方程的求解 文章目录 系列文章目录一、基本概念(一)极大似然估计和EM算法(二)EM算法的基本思想(三)定义1、缺失数据, 边际化和符号2、Q函数3、混合高斯模型(Gaussian Mixture Model,简称GMM)4、一般混合模型 三、收敛性(一)琴生不等式(Jensen’s inequality)(二) EM 算法的收敛性质(三)MM 算法 (
从高斯分布、机器人误差、EM算法到小球检测
Coursera上的课程(Robotics: Estimation and Learning),感觉讲得特别棒,写下自己的理解。 高斯分布被广泛应用于对机器人误差的建模。在这篇笔记中,我们将会: 介绍如何使用一元高斯分布、多元高斯分布和高斯混合模型对机器人误差进行建模。介绍求解这些高斯分布的算法。以小球检测这一实际应用来实践我们的模型和算法。 1. 一元高斯分布 在这一节我们将介绍如何使用
px, em, rem, vw, vh, vmin, vmax的含义
vw 相对于视窗的宽度:视窗宽度被平均分为100vw,即width:1vw相当于width:1%,此1%不是父元素的1%而是视窗的1%。 vh 相对于视窗的高度:视窗高度被平均分为100vh vmin vw和vh中较小的那个被均分为100单位的vmin,应用场景举例:用于移动设备横屏竖屏的显示时 vmax vw和vh中较大的那个被均分为100单位的vmax 注意,“视区”所指为浏览器内部的
最大似然估计、梯度下降、EM算法、坐标上升
机器学习两个重要的过程:学习得到模型和利用模型进行预测。 下面主要总结对比下这两个过程中用到的一些方法。 一,求解无约束的目标优化问题 这类问题往往出现在求解模型,即参数学习的阶段。 我们已经得到了模型的表达式,不过其中包含了一些未知参数。 我们需要求解参数,使模型在某种性质(目标函数)上最大或最小。 最大似然估计:
Oracle10g重建EM 报ORA-20001: SYSMAN already exists
10g重建EM 报ORA-20001: SYSMAN already exists 解决方法: Logon SQLPLUS as user SYS or SYSTEM, and drop the sysman account and management objects: SQL> drop user sysman cascade; SQL> drop role MGMT_US
期望最大化算法(expectation maximization,EM)
EM算法是一种迭代算法,用于含有隐变量(hidden variable)或缺失数据(incomplete-data)的概率模型参数的极大似然估计。EM算法被广泛用于高斯混合模型(Guassian Mixture Model,GMM)和隐马尔可夫模型(Hidden Markov Model,HMM)的参数估计。每次迭代分为两步:E步,求期望;M步,求极大。概率模型有时既包含观测变量(observab