本文主要是介绍A Community-Aware Framework for Social Influence Maximization，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Abstract
我们考虑影响力最大化（IM）问题，即在社交网络中选择 k 个种子节点，以使受影响的节点的预期数量最大化的任务。
我们提出了一个社区意识分而治之的框架，其中包括（i）学习社交网络的固有社区结构，（ii）通过解决每个社区的影响力最大化问题来生成候选解决方案，以及（iii）选择最终的解决方案使用新颖的渐进预算方案的种子节点集。我们对现实世界社交网络的实验表明，所提出的框架在运行时间方面优于标准方法，在影响力方面优于启发式方法。我们还研究了社区结构对所提出框架性能的影响。我们的实验表明，具有更高模块化程度的社区结构使得所提出的框架在运行时和影响力方面表现更好。
索引术语——社交网络、影响力最大化、病毒式营销、社区发现、子模块最大化。
I. INTRODUCTION
A. Motivation
社交媒体的出现改变了传统营销策略的设计方式[1]。公司现在更愿意分配很大一部分营销预算来通过大型社交媒体平台推动销售。利用社交媒体进行促销营销的方式有多种。例如，在访问量最大的社交平台上做广告、制作社交媒体页面进行品牌推广和传播有关产品的信息等。促销营销的更复杂的方法是利用社交网络的动态来识别合适的个人受到激励以在整个网络中获得最大的影响力。
在社交媒体营销的背景下，多明戈斯和理查森提出了影响力最大化（IM）问题[2]：“如果我们能够尝试说服社交网络中的一小部分人采用新产品或创新，目标是为了引发大量的进一步收养，我们应该针对哪一组人？”形式上，它的任务是在社交网络中选择 k 个种子节点，以使网络中受影响节点的预期数量（在某种影响力传播模型下）（称为影响力）最大化。肯佩等人。 [3]表明影响力最大化问题是NP-Hard问题。该问题已在文献中得到广泛研究，并提出了几种解决该问题的方法。有些方法提供了接近最优的解决方案，但运行时间成本高昂。另一方面，一些方法速度更快，但是是启发式的，即没有近似保证。
出于解决准确性和运行时间之间的这种权衡的想法，我们提出了一个社区意识的分治框架来提供一个高效的解决方案。所提出的框架在运行时间方面优于标准方法，在影响方面优于启发式方法。
B. Literature Review
在文献中，研究人员尝试使用多种方法来解决影响最大化（IM）问题。我们讨论相关方法如下。
1）简单启发法：程度中心性可能是量化网络中个体影响力的最简单方法[3]。 Chen 等人观察到许多最中心的节点可能聚集在一起，因此完全没有必要针对所有节点。 [4]提出了度折扣启发式。这些启发式方法既简单又省时。然而，他们没有任何可证明的保证。
2）基于模拟的方法：基于模拟的方法假设网络中信息传播的基础模型，并通过使用昂贵的蒙特卡罗模拟评估不同的个体集合来选择有影响力的个体。在独立级联 [5]、[6] 和线性阈值 [7]、[8] 扩散模型（第 II-B 节中讨论）下，Kempe 等人。 [3]表明影响力最大化问题是NP-Hard问题。他们还建议使用一种高效的贪婪算法 [2]，这是由于 Nemhauser 等人的结果。 [9] 给出了解的 (1 − 1 e ) 近似。该算法的渐进运行时间为O(nk)。从渐近的角度来看，这种贪心算法是有效的，但从经验来看，昂贵的蒙特卡罗模拟会导致巨大的开销。莱斯科维奇等人。 [10]提出了CELF算法，该算法通过进一步利用子模性的性质来改进简单贪婪算法的经验运行时间。戈亚尔等人。 [11]提出了CELF++算法，该算法进一步改进了CELF算法的经验运行时间，进一步利用子模性的特性来避免CELF引起的边际增益的不必要的重新计算。请注意，CELF 和 CELF++ 都是贪婪算法，其渐近运行时间与 Kempe 等人提出的算法相同。 [3]，并且运行时增益只是经验性的。博格斯等人。 [12]提出了一种使用反向影响采样（RIS）的贪婪算法——一种有效估计种子集影响的方法。 CELF、CELF++ 和 [12] 具有与 Kempe 等人提出的相同的最坏情况运行时间 O(nk) 和近似比 (1 − 1 e )。 [3].洛菲塔尔.[13]提出了一种基于遗传算法的动态（随时间演变）网络的启发式算法。该方法涉及蒙特卡罗模拟并且没有任何近似保证。本文提出的框架还可能涉及蒙特卡罗模拟。但是，分而治之的策略使我们能够显着减少运行时间。
3）基于社区的方法：由于所提出的方法利用了网络固有的社区结构，因此我们如下讨论其他基于社区的影响力最大化方法。陈等人。 [14]在热扩散模型[15]下提出了两种方法，称为CDHKCut和CDH-SHRINK。他们进一步改进了他们的方法，提出了另一种称为CIM的方法[16]。博佐尔吉等人。 [17]提出了一种称为 INCIM 的方法，该方法仅适用于线性阈值扩散模型。此外，该方法涉及重叠社区检测，这与我们社区不重叠的工作相反。博佐尔吉等人。 [18]还开发了一种在竞争线性阈值模型下竞争影响最大化的方法[19]。尚等人。 [20]在独立级联扩散模型和加权级联边缘权重模型下提出了一种称为CoFIM的方法。与这些方法相反，我们的方法不依赖于扩散模型的选择。黄等人。 [21]提出了一种称为 CTIM 的基于数据的方法，它需要潜在的操作日志和项目主题相关性。
4）基于数据的方法：在存在一些涉及现实世界扩散轨迹的观测数据或行动日志的情况下，可以通过直接从数据估计影响来完全避免昂贵的蒙特卡罗模拟。戈亚尔等人。 [22]没有使用传播模型，而是提出了一种新颖的数据库方法来引入称为信用分配模型的模型，该模型直接利用现实世界数据的传播轨迹并学习网络中的影响流。彭等人。 [23] 和邓等人。 [24]分别研究了时间约束和节点特征下信用分配模型的变体。所提出的方法不涉及任何观测数据。然而，这是一项潜在的未来工作。
5）在线方法：最近，焦点还集中在以在线方式解决影响力最大化问题，其目标是在接收即时反馈的同时最大化不同时间选择的种子集的累积观察到的影响力。基于半老虎机反馈[25]、[26]、[27]、[28]、[29]和全老虎机反馈[30]、[31]，方法有所不同。所提出的方法不是在线方法。然而，这是一项潜在的未来工作。
C. Contribution
在第 I-B 节中，我们讨论了 CELF++ [11] 算法比简单的贪婪算法 [2]、[3] 更快。但是在整个网络中执行大量扩散的成本仍然存在。出于以省时的方式解决影响力最大化问题的想法，我们提出了一种社区意识分而治之的框架，其中包括（i）学习社交网络的固有社区结构，（ii）生成候选解决方案通过解决每个社区的影响力最大化问题，以及（iii）使用新颖的累进预算方案从候选解决方案中选择最终一组要受到激励的个人。我们的方法也可以使用蒙特卡罗模拟，但与整个网络相比，我们将它们限制在每个社区内，与 CELF++ 算法相比，这节省了运行时间。
与其他基于社区的方法相比，所提出的框架在以下方面具有新颖性。它不限于特定的扩散和/或边缘权重模型。在步骤（i）中，候选解决方案集是由来自每个社区的解决方案的所有组合生成的。在步骤(ii)中，通过在受预算约束的候选解决方案上求解整数线性规划(ILP)来执行最终种子选择。我们提出了一种有效的累进预算方案来有效地解决步骤（iii）中的 ILP。我们提供了该方案的正确性证明，该方案利用了影响力的子模块性（在第二节中定义）。
我们在现实世界的社交网络上进行了实验，表明所提出的框架在运行时和启发式方法的影响方面优于基于模拟的方法。我们研究社区结构对所提出框架性能的影响。我们的实验表明，具有较高“模块化”（在第三节中定义）的社区结构使得所提出的框架在运行时间和影响力方面表现更好。
D. Organization
本文的其余部分安排如下。在第二节中，我们讨论预备知识并提出问题。在第三节中，我们讨论我们的方法。在第四节中，我们讨论针对不同社交网络进行的实验。第五节总结了本文并讨论了未来的方向。
II. PRELIMINARIES AND PROBLEM FORMULATION
在本节中，我们讨论一些预备知识并阐述本文感兴趣的问题。有关整篇论文中使用的重要符号，请参阅表 IV（附录 C）。
A. Submodularity
设 Ω 表示 n 个元素的基本集合，O = 2Ω 为 Ω 的所有子集的集合。
如果集合函数 f : O→R 满足自然的“收益递减”属性，则称其为子模：将元素 v 添加到asetS ∈Si 的边际收益至少与将相同元素 v 添加到一个超集 T ∈Oof S。形式上，对于任何集合 S，T ∈O 使得 S ⊆ T , f 满足
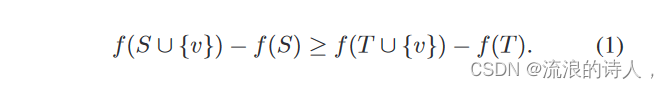
集合函数 f : O→R，如果对于任意集合 S, T ∈O 使得 S ⊆ T , f 满足，则为单调（非递减）
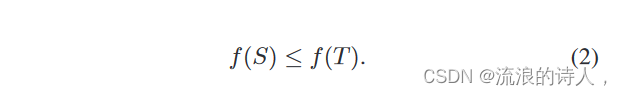
B. Diffusion Models and Social Influence
扩散模型描述了社交网络中级联如何发生。出于我们研究的目的，我们重点关注扩散的独立级联 [5]、[6] 和线性阈值 [7]、[8] 模型
在独立级联模型中，给定图 G =(V, E)，该过程从时间 0 开始，具有一组初始活动节点 S，称为种子集。当节点 v ∈ S 在时间 t 首次变为活动状态时，它将有一次机会激活每个当前不活动的邻居 w，它以 pv,w 的概率成功（与迄今为止的历史记录无关）。如果 w 有多个新激活的邻居，则它们的尝试按任意顺序排序。如果 v 成功，那么 w 将在时间 t +1 时激活；但无论v是否成功，它都不能在后续回合中进一步尝试激活w。该过程将一直运行，直到无法进一步激活为止。
在线性阈值模型中，给定图 G =(V, E)，节点 v 根据权重 pv,w 受到每个邻居 w 的影响，使得 Σ w∈∂v pv,w ≤ 1，其中 ∂v 表示v的邻居集合。每个节点v从区间[0,1]中统一选择一个阈值θv；这表示 v 的邻居的加权分数必须变得活跃才能使 v 变得活跃。该过程从随机选择节点阈值和一组初始活动节点 S（称为种子集）开始。在步骤 t − 1 中处于活动状态的所有节点都保持活动状态，并且我们激活任意节点 v其活跃邻居的总权重至少为 θv。该过程将一直运行，直到无法再激活为止。
请注意，这两个扩散过程都是渐进的，即节点可以从不活动状态切换到活动状态，但不会向另一个方向切换。在级联中的任何时间 t，每个节点 v ∈ V 可以是活动的或不活动的。我们将该过程表示为
集合 S 的影响 σ(S) 定义为级联末端的预期活动节点数（表示为时间 T ），假设 S 是初始节点集。
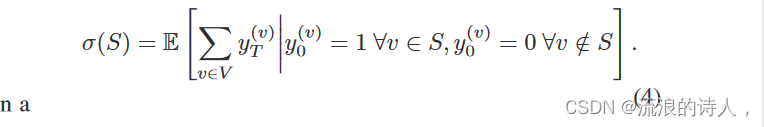
肯佩等人。 [3]表明，在独立级联和线性阈值模型等常见扩散模型下，σ(S)是单调非递减子模集函数。
C. Problem Statement
对于给定的整数预算 k，我们感兴趣的是找到节点集 V 的 k−节点子集，它对 V 的所有可能的 k−节点子集具有最大影响。形式上，影响力最大化（IM）问题定义为
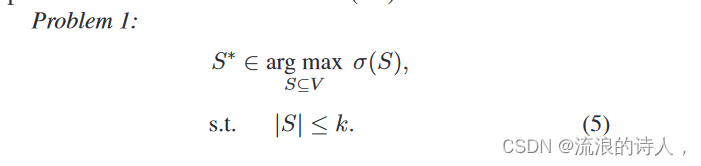
III. METHODOLOGY
如前所述，基于模拟的方法面临着在整个网络中进行扩散以估计不同候选解决方案的影响的巨大开销。受以高效的方式解决（5）中定义的影响力最大化问题的想法的启发，我们提出了一个社区意识的分而治之框架。所提出的框架试图通过将给定网络划分为多个子网络来限制扩散到原始网络的某些子网络而不是整个网络，从而降低模拟成本。由于大多数现实世界的网络都表现出某种社区结构，因此可以通过学习其固有的社区结构来获得网络的这种划分。所提出的框架涉及（i）学习社交网络的固有社区结构，（ii）通过解决每个社区的影响力最大化问题来生成候选解决方案，以及（iii）从候选解决方案中选择最终要激励的个体集使用新颖的累进预算方案。
算法 1 概述了本文提出的框架。它使用三个子例程，这些子例程将在以下小节中进行解释。
A. Learning the Inherent Community Structure of the Social Network
对于给定的社交网络 G =(V, E)，我们使用某种社区检测方法获得 V 的硬分区 {V1,...,Vc}。通过硬划分，我们的意思是 Vi ∩ Vj = φ ∀i = j = 1,...,cand ⋃ i Vi = V 。Let|Vi| = ni 是第 i 个群落的大小，i =1,...,c, Σc i=1 ni = n。定义 Gi =(Vi,Ei)，其中 Ei 是 E 中属于 Vi 中节点对的边集。我们将 {G1,...,Gc} 称为网络分区。
大多数社区检测方法试图在网络中找到社区，使得社区内的节点比社区之间的节点更加“连接良好”。测量网络中节点连通性的方法通常有所不同。常见的方法有Louvain [32]、标签传播[33]和Girvan-Newman算法[34]。
算法 2 概述了社区检测步骤。
1）网络分区的质量：网络分区的质量可以使用模块化分数来衡量[35]，[36]。网络分区的模块性分数定义为给定组内的边的分数减去边缘随机分布时的预期分数。对于网络分区 {G1,...,Gc}，模块性 [36] 定义为
其中 Li 是 Gi 中节点对之间的边数，δi 是 Gi 中节点的度数之和。
模块化得分衡量社区检测算法划分网络的程度。较高的模块化值对应于每个社区内具有较高连通性的网络分区。
2）社区检测方法：我们讨论一些常用的社区检测方法。 Louvain方法[32]首先通过在所有节点上局部优化模块化来获得小社区。然后将每个小社区视为单个节点并重复之前的步骤。标签传播 [33] 从具有社区标签的节点的（通常很小）随机子集开始。然后，该算法迭代地将标签分配给先前未标记的节点。 Girvan-Newman 方法 [34] 使用一种称为“介数”的度量。将边 [34] 的介数定义为沿其运行的任何一对节点之间的最短路径的“权重”之和。如果任意两个节点之间有 d 条不同的最短路径，则每条路径的权重设置为 1/d。 Girvan-Newman方法[34]方法涉及以下步骤。
1）首先，计算网络中所有现有边的介数。
2) 接下来，删除介数最高的边。
3) 最后，重新计算上一步中受移除影响的所有边的介数。
4) 重复前两步，直到没有边缘为止。
B. Generating Candidate Solutions by Solving the Influence Maximization Problem for Each Community
对于每个社区，我们通过仅保留该社区中的节点以及与它们相关的所有边来找到 G 的子图，然后使用标准方法为该子图找到大小最大为 k 的“最佳”种子集。令 Si,j 为社区 i 中大小为 j (j =1,...,k) 的最佳种子集，σi(Si,j) 为其在社区 i (i =1,...,c) 内的影响力）。
分别解决不同社区而不是整个网络的影响最大化问题会带来经验运行时间的收益，因为与整个网络相比，社区内的扩散长度要短得多。算法 3 概述了标准影响力最大化步骤。
C. Selecting the Final Seed Set
我们从 {Si,j : i =1,...,c; 中选择尽可能多的集合； j = 1,...,k}，它们之间没有重复元素，因此它们的影响之和最大化，并且它们的并集恰好有 k 个元素。使用该并集作为 (5) 的解。形式上，我们正在求解以下整数线性规划（ILP）。
一般来说，解决 ILP 是一个 NP 完全问题 [37]。然而，影响的子模性使我们能够在多项式时间内求解 (6) 中的 ILP。
1）渐进预算：根据子模块性的定义，我们知道种子集中每增加一个节点所带来的边际影响力收益都会递减。因此，我们可以在 S 中的集合之间逐步分配预算一旦为某个集合分配了预算，它就会保留在所有最终选择的集合的列表中。
算法 4 概述了算法 1 中使用的渐进预算子例程。
定理 1：渐进预算解决了 (6) 中的 ILP。
证明：由于影响的子模性，证明如下。 (6)中的ILP试图选择唯一的Si,j，使得它们所有的基数之和等于k并且它们的影响之和最大化。我们知道 Si = {Si,j : j =1,...,k} 是社区 i 内影响力最大化问题的贪心解。因此，由于子模性，我们有 σi(Si,1) − σi(Si,0) ≥ ... ≥ σi(Si,k) − σi(Si,k−1) ∀i。利用这一特性，渐进式预算算法通过比较不同选择之间影响力的边际改进，迭代地构建一组独特的 Si,j。因此，渐进预算确实解决了（6）中的 ILP。
附录 B 提供了累进预算的说明性示例
D. Computational Complexity Analysis
我们现在分析所提出的框架（算法 1）的计算复杂性。所提出框架的运行时间是三个步骤所用时间的总和。这取决于社区检测方法的选择以及针对每个社区解决IM的解决方法。我们分析每一步涉及的运行时间如下
1）学习社交网络固有的社区结构：
本文考虑的不同社区检测算法的最坏情况运行时间如下：Louvain方法为O（n log n）[32]，标签传播为O(n + |E|) [33]，Girvan-Newman 方法为 O(n|E|2) [34]。
2) 通过解决每个社区的影响力最大化问题生成候选解决方案：
如果我们使用 CELF++ 来解决 c 个不同社区的 IM，那么我们正在解决 c 个问题，即从 ni 个节点中为每个社区找到 k 节点子集，i = 1， ...,c.对于theith社区，CELF++迭代构建k节点子集如下。首先，通过评估基数一的所有 ni 个子集来找到最佳单个节点。接下来，通过评估（最多）先前选择的最佳个体和附加节点的所有 ni − 1 个子集，找到在存在最佳个体节点的情况下具有最高边际影响力的节点。 CELF++然后以相同的方式不断向前一个集合添加节点，直到当前集合的大小为k。最坏情况下，第 k 步评估的 k 节点子集的数量为 ni − (k − 1)。因此，最坏情况下评估的子集数量为
相反，如果我们对整个网络使用CELF++，那么在最坏情况下评估的子集总数为
通过比较（8）和（9），我们观察到，与对整个网络使用 sol 方法相比，所提出框架的GenerateCandidates 步骤通过附加因子 (c − 1)k(k) 实现了更低的运行时间− 1)/2。此外，由于 ni ≤ n ∀i =1,…,c，在任何社区内使用蒙特卡罗模拟评估节点子集时的扩散长度总是比在整个网络中执行相同操作时更小。这进一步减少了生成候选步骤的运行时间
3）使用渐进预算的最终种子集选择：
最终种子集选择的渐进预算方法解决了“找到c个元素的最大值”k次。因此，渐进预算最坏情况的运行时间是 O(ck)。
在实践中，由于昂贵的蒙特卡罗模拟，解决每个社区的 IM（使用基于模拟的 sol 方法）是花费最多时间的步骤。从这个意义上说，与使用相同的基于模拟的原始网络解决 IM 的运行时间相比，所提出的框架（使用基于模拟的 sol 方法）解决每个社区的 IM 的最坏情况运行时间较低。溶胶法。
IV. EXPERIMENTS
我们使用现实世界的社交网络评估了所提出的框架的性能。我们讨论用于实验的网络数据，列出选择用于比较的算法，提供实验细节、展示结果和讨论。
A. Network Data
我们使用 4 个真实世界的社交网络进行实验。该数据可在 https://snap.stanford.edu/data/Stanford Large Network Dataset Collection [38] 获取。
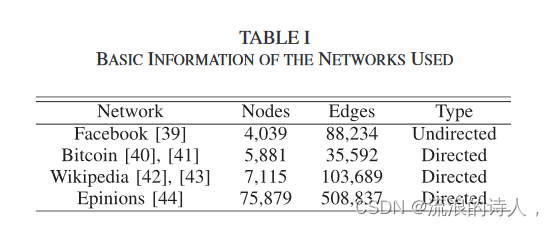
表 I 提供了每个网络的节点数、边数和类型。
Facebook 网络是一个由 Facebook 的“圈子”（或“朋友列表”）组成的数据集[39]。比特币网络是一个谁信任谁的网络，由在比特币场外交易平台上使用比特币进行交易的人们组成[40]，[41]。维基百科网络是一个谁投票谁成为管理员的网络[42]，[43]。 Epinions 是一个名为 Epinions 的通用消费者评论平台的谁信任谁的在线社交网络[44]。
对于无向网络，每条边都被两条有向边替换。对于边权重，使用两个模型，即加权级联模型 [3]，其中对于每个节点 v ∈ V，进入 v 的每条边的权重设置为 1/in- Degree(v) 和三价模型 [22]，其中每个边权重都是从一小组常量 {0.1, 0.01, 0.001} 中均匀随机抽取的。然而，对于扩散的线性阈值模型，仅使用加权级联模型作为边权重，因为三价模型不一定保持入射到节点上的所有边的权重之和小于或等于1。
B. Algorithms
我们将所提出的社区感知框架（Community-IM）与以下算法进行了比较。
1）CELF++[11]，一种基于模拟的贪心算法。
2）CoFIM [20]，一种社区感知启发式算法。
3）DSGA[13]，一种基于遗传算法的方法。
4）Degree-Discount [4]，一种启发式算法。
5）出度，一种启发式算法，其中对于预算k，选择topk个出度节点。我们选择上述算法的原因如下
CELF++ 是最先进的基于模拟的算法。 CoFIM 是一种具有社区意识的启发式方法，在带有加权级联 [3] 边缘权重模型的独立级联扩散模型下具有理论保证。 DSGA [13] 是一种最新的基于遗传算法的方法，使用蒙特卡罗模拟。学位折扣和出学位是一些最简单但最强大的启发式方法。
在第一节下的文献综述小节中讨论的 INCIM 算法 [17] 可能是我们在线性阈值扩散模型下进行比较的社区感知基线，但它使用与我们的方法相反的重叠社区结构。
请注意，CoFIM 算法仅针对具有加权级联边缘权重模型的独立级联扩散模型而开发。然而，为了进行实证比较，我们也将其应用于扩散模型和边缘权重模型的其他选择。
作为 Community-IM 的一部分，我们分别使用 Louvain 方法 [32] 作为 com 方法，使用 CELF++ [11] 作为 sol 方法，用于社区检测和生成候选者。我们还研究了固有的社区结构对所提出框架性能的影响。为此，我们使用通过第 III-A2 节中讨论的社区检测算法学习到的社区结构。为简洁起见，我们仅考虑加权级联边权重模型下的 Facebook 网络，以研究社交网络学习社区结构的效果。
C. Experimental Details
我们使用预算 k =1, 5, 10,...,100 来比较不同的算法。然而，对于 DSGA [13]，由于其运行时间较长，我们仅使用预算 k =1, 20, 40,...,100。任何种子集的影响被估计为从相同种子集开始的底层扩散的 1,000 个不同蒙特卡罗模拟中的平均活跃节点数。对于任何网络，如果社区检测方法返回的一些社区的个体大小低于网络中节点数量的 1%，那么我们将它们全部合并为一个社区。我们这样做是为了避免出现太多的小社区。
实验在配备 2.6 GHz 24 核 Intel Xeon Gold Sky Lake 处理器和 96 GB 内存的计算机上进行。我们使用 Python 来实现。 CELF++和CoFIM的作者提供的源代码是用C++编写的。本文的数据和源代码可在 https://github.com/abhishekumrawal/CommunityIM 获取
D. Results
对于不同扩散模型和边权重模型下的不同网络，图 1-3 显示了使用不同算法对不同 k 值选择的种子集的影响。表 II 显示了使用 CELF++、Community-IM、CoFIM 和 DSGA 选择的大小为 100 的种子集的影响。表 III 显示了 k = 100 时 CELF++、Community-IM、CoFIM 和 DSGA 的经验运行时间。此外，不同扩散模型下的 Facebook 网络和使用不同社区检测方法的加权级联边缘权重模型的结果为附录 C 中提供。
E. Discussion
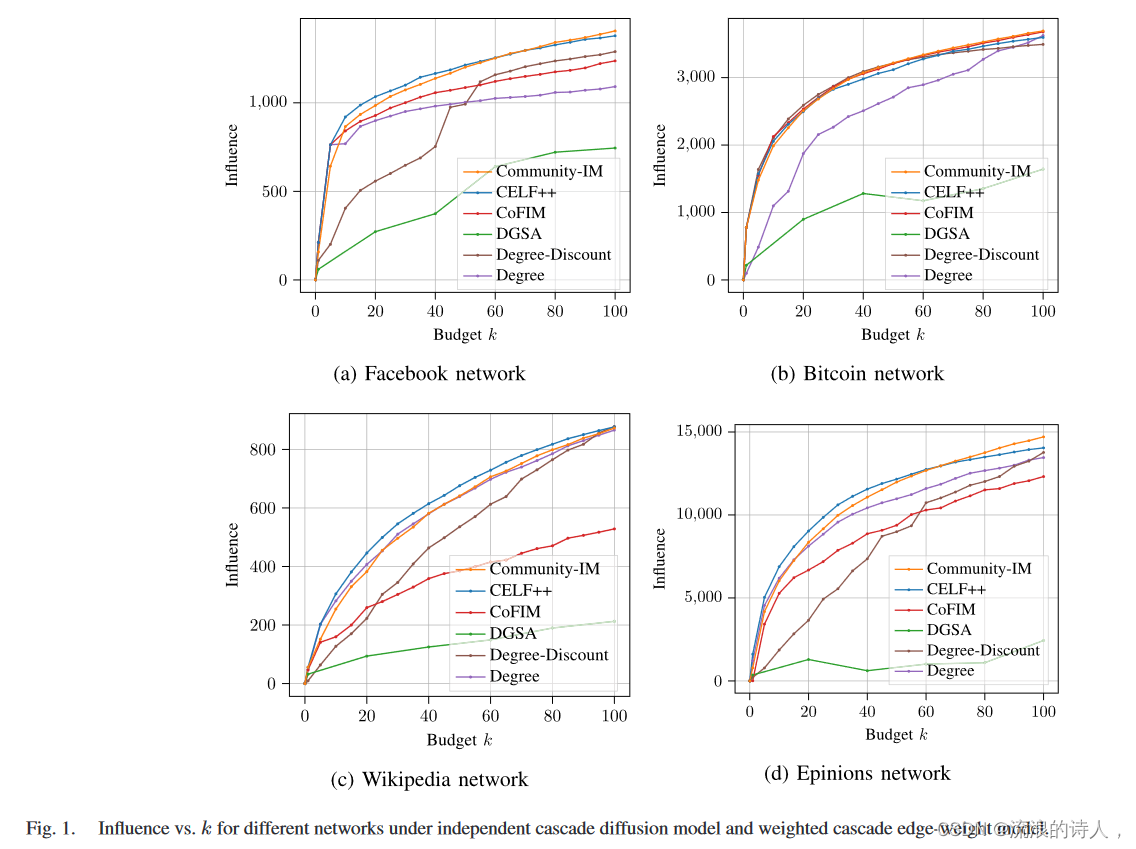
图 1. 独立级联扩散模型和加权级联边权重模型下不同网络的影响与 k 关系。
图1（a）显示，对于独立级联扩散模型和加权级联边权重模型下的Facebook网络，当预算k达到60时，Community-IM的影响力略低于CELF++的影响力。然而，当预算 k 大于 60 时，Community-IM 的影响与 CELF++ 的影响相同或更高。此外，对于预算 k 的所有值，与除 CELF++ 之外的所有其他方法的影响相比，Community-IM 的影响要高得多。图1(d)提供了独立级联扩散模型和加权级联边权重模型下的 Epinions 网络具有类似的见解。图 2（a）为独立级联扩散模型和三价边权重模型下的 Facebook 网络提供了类似的见解。
图1（b）显示，对于独立级联扩散模型和加权级联边权模型下的比特币网络，当预算k达到60时，除了DSGA和Degree的影响之外，所有方法的影响都非常接近。 - 折扣比其他的低。然而，当预算 k 大于 60 时，Community-IM 的影响往往会超过除 CoFIM 之外的所有其他方法的影响。图1（c）显示，对于维基百科网络，对于预算k的所有值，Community-IM的影响力略低于CELF++，而Community-IM的影响力高于CoFIM、DSGA 、独立级联扩散模型和三价边权重模型下的度数折扣和度数。
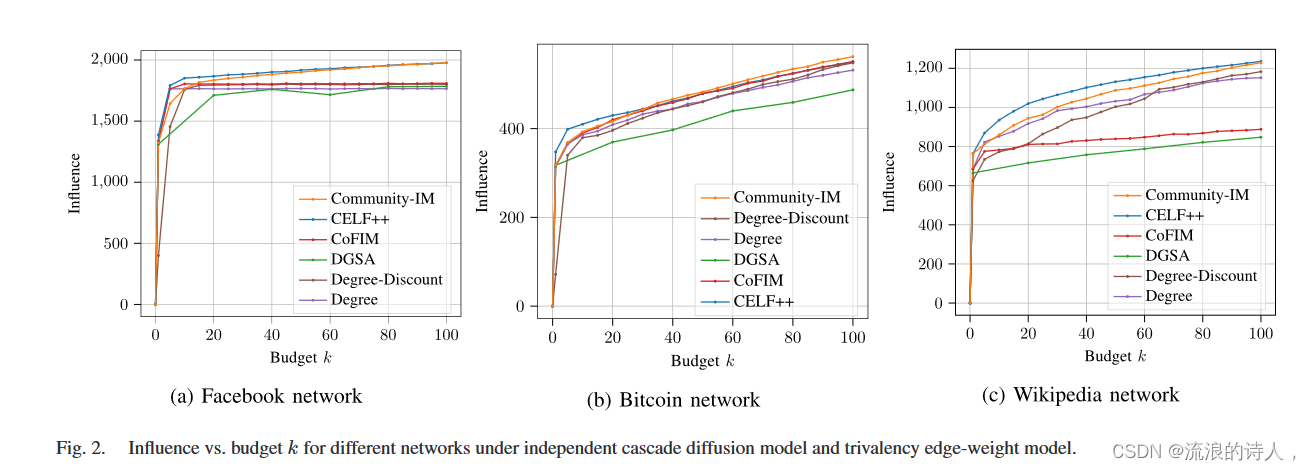
图2.独立级联扩散模型和三价边权重模型下不同网络的影响与预算k。
图2（b）显示，对于独立级联扩散模型和三价边权重模型下的比特币网络，当预算k达到30时，Community-IM的影响略低于CELF++的影响。然而，当预算 k 大于 30 时，Community-IM 的影响高于 CELF++。此外，与 CoFIM、DSGA、Degree-Discount 和 Degree 相比，Community-IM 的影响力更高。图2（c）显示，对于独立级联扩散模型和三价边缘权重模型下的维基百科网络，对于预算k的所有值，Community-IM的影响力略低于CELF++的影响力。然而，Community-IM 和 CELF++ 的影响力之间的差距随着预算 k 的增加而减小。此外，与 CoFIM、DSGA、Degree-Discount 和 Degree 相比，Community-IM 的影响力更高。图 3(c) 为维基百科网络在线性阈值扩散模型和加权级联边权重模型下提供了类似的见解。
图 3. 线性阈值扩散模型和加权级联边权重模型下不同网络的影响与预算 k 的关系。
图3（a）显示，对于线性阈值扩散模型和加权级联边缘权重模型下的Facebook网络，当预算k达到15时，Community-IM的影响略低于CELF++的影响。然而，当预算 k 大于 15 时，Community-IM 的影响高于 CELF++。此外，与 CoFIM、DSGA、Degree-Discount 和 Degree 相比，Community-IM 的影响力更高。
图3（b）显示，对于线性阈值扩散模型和加权级联边权重模型下的比特币网络，当预算k达到40时，Community-IM的影响为略低于 CELF++。然而，当预算 k 大于 40 时，Community-IM 的影响高于 CELF++。此外，请注意，当预算 k ≥ 30 时，CoFIM、Degree-Discount 和 Degree 的影响高于 CELF++，但同时 Community-IM 的表现更好或与 DSGA、Degree-Discount 和 Degree 一样好。
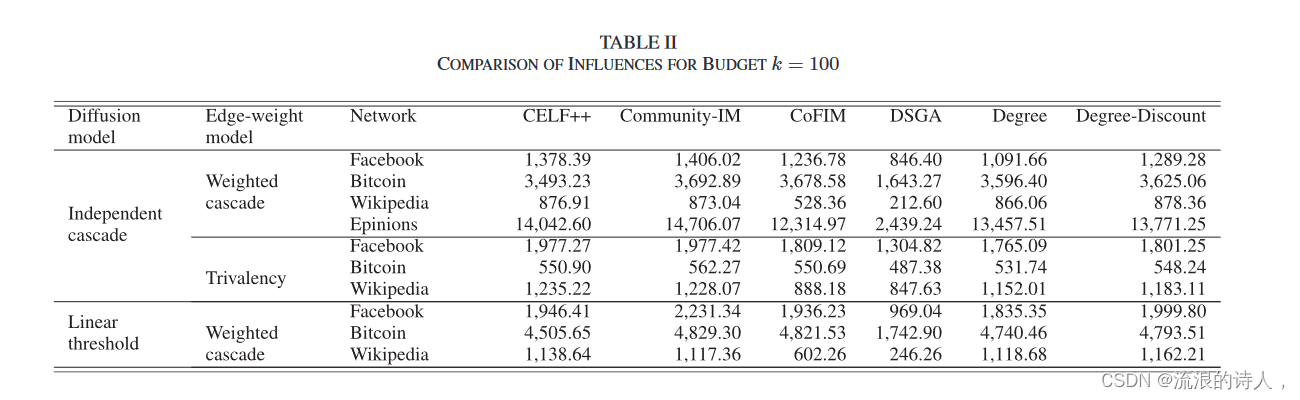此外，表 II 显示，对于每个网络，使用 Community-IM 选择的大小为 100 的种子集的影响非常接近甚至更好于不同扩散模型和边缘权重模型下的 CELF++。此外，
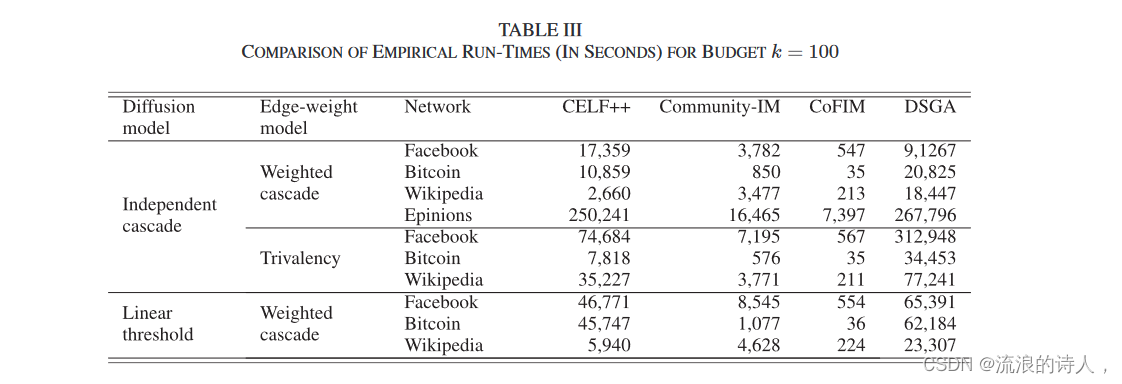表 III 显示，与 CELF++ 算法相比，在所有扩散模型和边权重模型选择下，所提出的社区意识框架在经验运行时间方面带来了巨大的节省。如前所述，Community-IM 在不同网络、扩散模型和边权重模型中比 CELF++ 和 DSGA 快得多。从表 III 中，我们还注意到，运行时间的增益在扩散模型和边权重模型之间存在差异。增益最高的是具有三价边权重模型的独立级联模型，而增益最小的是具有加权级联边权重模型的独立级联模型。
表VII（附录C）显示，对于Facebook网络，使用Community-IM选择的大小为50的种子集的影响大约等于CELF++对于不同扩散模型和加权级联下社区检测方法的不同选择的影响边权重模型。此外，表七和表八（附录C）表明，随着分区模块化和社区数量的增加，Community-IM 与 CELF++ 相比，在影响力和运行时间方面的性能有所提高。从表VII和表VIII（附录C）中，我们还注意到Louvain方法是社区检测方法的最佳选择，而Girwan-Newman方法表现最差。 Louvain方法将图划分为18个社区，最大的社区有523个节点，大约是整个网络大小的10%。因此，Community-IM 不会遇到任何巨大的组件，并且完成得更快。与此相反，Girwan-Newman算法将网络仅划分为两个社区，最大的社区有3,833个节点，非常接近整个网络的规模，因此Community-IM方法需要花费大量时间来完成。
我们还观察到，对于预算 k 的所有值，Girwan-Newman 算法对 Community-IM 的影响非常接近 CELF++，这可以通过以下事实来解释：Girwan-Newman 算法将整个网络划分为两个社区，其中一个社区是整个网络的一个巨大的互联组成部分。另一方面，对于预算 k 的所有值，使用 Louvain 算法的 Community-IM 和使用标签传播算法的 Community-IM 的影响彼此非常接近，这可以通过以下事实来解释：这两种方法非常接近。
总体而言，我们观察到，与最先进的基于模拟的算法 CELF++ 相比，所提出的框架以影响力损失最小的方式节省了运行时间，并且与其余的算法。
V. CONCLUSION AND FUTURE WORK
为了解决社交网络影响力最大化的问题，我们利用网络固有的社区结构，提出了一种新颖的社区感知框架，用于通过社交网络快速最大化影响力的传播。根据我们的实验，我们得出的结论是，所提出的框架在经验运行时间方面优于基于模拟的算法，在影响力方面优于启发式算法。由于所提出的方法利用了网络固有的社区结构，我们还研究了社区结构对我们框架性能的影响。根据我们的实验，我们得出的结论是，具有更高模块化程度的社区结构使得所提出的框架在运行时和影响力方面表现更好。在本文考虑的方法中，我们发现 Louvain 算法 [32] 对于影响力最大化问题是最好的。
我们指出我们的方法的两个局限性。首先，我们的方法要求在步骤（i）中学习的社区不重叠。然而，一般来说，现实世界的社交网络可能具有重叠的社区。其次，我们的方法在步骤（ii）中生成候选解决方案时没有明确考虑社区间的影响。未来，我们希望扩展我们的方法，使其能够处理重叠的社区结构，并明确地考虑社区间的影响。未来的其他方向是将所提出的社区感知框架扩展到竞争影响力最大化[45]、基于数据的影响力最大化[22]和全强盗在线影响力最大化[30]、[31]。
这篇关于A Community-Aware Framework for Social Influence Maximization的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
