Influence blocking maximization on networks: Models, methods and applications

本文主要是介绍Influence blocking maximization on networks: Models, methods and applications，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

abstract

由于各种社会和贸易网络的不断出现，网络影响力分析引起了研究者的极大兴趣。基于不同的影响力传播模型，人们提出了许多网络影响力最大化的新模型和方法。作为传统影响力最大化问题的延伸和扩展，影响力封锁最大化问题已成为研究热点，并在物理学、计算机科学和流行病学等多个领域得到广泛应用。近年来，已经报道了影响块最大化问题的各种方法。然而，我们仍然缺乏从社交网络影响力分析方面系统分析影响力阻止最大化问题的方法论和理论进展的全面回顾。本综述旨在通过对影响力阻止最大化的理论和应用进行全面的调查和分析来填补这一空白。它不仅增进了对影响力最大化问题的理论理解，而且将为未来的研究提供参考。

关键词：复杂网络信息扩散扩散模型影响扩散影响最大化影响阻塞最大化

1. Introduction

近年来，随着复杂网络的蓬勃发展，网络拓扑和传播动力学的研究引起了研究者的极大兴趣[1,2]。影响扩散分析是复杂网络分析的一个重要领域。它提供了复杂网络中影响力最大化、影响力传播预测和影响力源定位的模型和方法。例如，影响力最大化（IM）是影响力传播分析中的一个基本问题[3]。 IM问题的目的是根据节点度或其他中心性度量等一定的度量来识别一些有影响力的节点（称为种子），以将影响力传播到复杂网络中的最大范围[4]。 IM为企业选择有说服力的用户以促使最大数量的顾客接受其商品提供了有效的途径。政治家可以利用即时通讯技术来选择有影响力的媒体向公众传播他们的政治观点。

在这篇综述文章中，我们将重点关注传统 IM 问题的延伸和扩展，即影响力阻塞最大化 [5,6]。由于复杂网络的开放性和高速性，各种负面影响，例如虚假信息和谣言，可以在用户中快速且广泛地传播[7]。虚假新闻会对新闻中的个人造成一定程度的伤害，并可能引发社会恐慌[8]。谣言可能会降低企业的信誉，并可能损害个人的声誉。此外，假新闻的传播可能会导致社交网络的声誉和安全严重受损。为了有效阻止复杂网络上负面影响的传播，一般的方法是选择一些有影响力的个体在复杂网络上传播真实的消息[9]。如果用户收到真实信息并改正虚假信息，就不会再受到有害信息的影响。因此，在复杂网络中，积极信息的传播可以阻止消极信息的传播。这就是影响力阻塞最大化问题（IBM）。对于给定的扩散模型，IBM问题的目标是找到一组积极的种子来尽可能地阻止消极影响。

影响力阻断最大化可以应用于许多领域，例如谣言检测和控制[10,11]、假新闻监控[12,13]、防疫[14,15]、市场策略设计[16,17]、意见形成[18,19]等等。例如，当有关公司产品的负面信息在社交网络中传播时，公司可能会选择一些有影响力的用户来传播对该产品的正面评价，以抵消负面信息。当政治候选人试图阻止有关他或她的负面谣言时，或者当政府或公职人员试图阻止恐怖主义对公众健康和安全的威胁时，有必要在社交网络中选择适当的媒体来传播正面消息，以最大限度地减少负面消息。负面影响的蔓延。在与COVID-19（2019冠状病毒病）爆发后，我们必须对社交网络中的一些关键人群进行疫苗接种，以阻止病毒的传播[20]。

除了影响阻止最大化的广泛应用之外，它在复杂网络分析中也获得了突出的作用，主要是由于三个因素：（1）检测负面影响阻止最大化的正种子需要网络传播模型来描述两者的同时传播网络中的积极和消极影响。 (2)网络负面影响源深刻影响封锁结果。因此，影响力阻塞最大化问题为影响力源识别提供了重要的研究平台。 (3)由于影响力阻塞最大化需要估计负面影响和正面影响的传播，因此影响力阻塞最大化为影响力预测提供了重要手段。

近年来，已经报道了影响块最大化问题的各种方法。然而，我们仍然缺乏从社交网络影响力分析方面系统分析影响力阻止最大化问题的方法论和理论进展的全面回顾。最近发表了一些关于谣言检测和阻止的评论文章[21,22]。尽管谣言拦截问题在某种程度上与影响力拦截最大化问题相似，但这些综述文章的讨论并不能涵盖影响力拦截最大化问题的所有理论和技术问题。这些评论文章中探讨的方法在三个方面不适用于影响力阻塞最大化问题：（1）为了解决影响力阻塞最大化问题，必须考虑网络的结构。但大多数谣言拦截方法只考虑谣言传播的路径，而没有参考网络的整体拓扑信息。 (2)在影响力阻止最大化问题中，检测积极种子用户传播积极信息以纠正和抵消消极影响。但大多数谣言拦截方法都是通过阻断谣言源头来阻止谣言的传播，而不考虑其传播的积极影响。 (3)一些谣言拦截工作侧重于谣言检测，如识别假新闻和检测谣言来源，而不是识别阻断谣言的积极种子。为了填补这些空白，这篇综述文章的目标是从物理学和跨学科的角度彻底回顾复杂网络中影响阻塞最大化的方法和理论方面。将特别强调基于统计物理工具、网络影响传播模型和流体力学的方法和理论发展。

总之，我们的综述旨在为所有对阻碍最大化的负面影响的实践和理论方面感兴趣的学者提供参考材料，由于该主题的受欢迎程度，这很可能使我们的综述被广泛的跨学科受众阅读。这个话题是及时的，因为影响力阻止最大化问题的研究近年来对现实社交网络中的影响力传播产生了许多引人注目的理论见解，但我们仍然缺乏一篇全面的综述文章来介绍影响力阻止最大化问题的最新进展和成果系统地。

本评论文章的其余部分组织如下。第 2 节将概述影响阻止最大化的理论基础，其中将观察其目标函数的单调性和子模特性。第 3 节将回顾影响力扩散的不同模型并对它们进行分类。第 4 节将回顾影响块最大化问题的方法，这些方法根据不同的标准分为不同的类别。在本节中，我们还对这些方法的性能进行了详细的分析和比较。第五节将重点讨论影响力封锁最大化在谣言抑制、疫情控制、竞争营销、网络社交媒体、计算机病毒预防、城市路网交通控制等领域的应用。第六节总结了本文，并给出了与本研究主题相关的未来挑战。

2. Theoretical studies of influence blocking maximization

2.1. Problem definition

社交网络可以建模为图 G = (V , E)，其中 V 表示网络中的节点集，E 表示节点之间的边集。设u和v为社交网络G中的两个节点，(u,v)εE表示有一条边连接u和v，它们之间的传播概率用pu,v表示。令SN为在网络G中传播负面影响的负面种子的集合。IBM问题是在网络中找到k个正面种子节点，使得它们能够最大限度地阻止网络中负面影响的传播。

图1 负面影响传播与抑制示意图。其中，红色节点代表网络通信中存在负面影响的节点，绿色节点是未受影响的健康节点，粉色节点是受到负面影响的节点。蓝色节点为选中的抑制节点，浅蓝色节点为抑制节点可以覆盖的节点。 (a) 负面影响未传播时的初始网络状态；(b) 随着时间变化，负面影响传播后的网络状态； (c) 原网络添加抑制节点后的状态； (d) 节点阻止负面影响传播的网络状态。

IBM 问题还有一些其他的表现形式。例如，Masahiro 等人。 [23,24]将该问题命名为污染最小化，即通过阻止网络中的一些链接来最大程度地减少计算机病毒或恶意谣言等不良对象在网络中的传播。布达克等人。 [6]将该问题命名为负面影响力限制，即采用正面影响力来抵消误导性信息的传播，使受负面影响力影响的节点最小化。 2012 年，He 等人。 [5]将此类问题称为影响力阻止最大化，即最大限度地抑制负面影响的传播。在这篇综述中，我们将此类问题统一命名为影响力阻塞最大化（IBM）。图1展示了IBM问题中负面影响传播与抑制的示意图。从图1（b）可以看出，如果不抑制负面影响，网络中的大多数节点都会受到负面影响。然而，从图1（c）和（d）可以看出，通过选择一些积极的种子作为抑制节点，可以减少网络中负面影响的传播

定义1. 阻塞集：对于网络G，在给定的影响力传播模型下，设负种子集为SN ，正种子集为SP 。集合 SP 中的正种子的阻塞集被定义为当没有正种子时可以受到 SN 负面影响而当正种子集是 SP 时不能受到 SN 负面影响的节点的集合。我们用 IBS(SP , SN ) 来表示 SP 中的正种子对 SN 的负面影响的阻塞集。

定义2.阻塞影响：正种子集SP对SN的负影响的阻塞影响是阻塞集IBS(SP , SN )大小的期望：

定义3.影响力阻塞最大化：对于给定影响力传播模型下的网络G，设负种子集为SN，并设置一个正整数k。影响块最大化问题是找到满足 SP ⊆ V 和 |SP | 的正种子集 SP ≤ k，从而使阻塞影响σ (SP , SN )最大化，即找到最优的正种子集S* P ，使得：

2.2. Properties of the problem

在IBM问题中，影响函数σ(·)在IC和LT扩散模型下与正集SP是单调且子模的[5]。基于 σ (SP , SN ) 的单调性和子模性，利用贪心算法可以得到 (1 − 1/e) 的近似解

2.2.1. Monotonicity

定义4.单调性：设f(S)是集合的函数。令 S 和 T 为两个集合，使得 S ⊆ T 。如果满足以下方程，函数 f(S) 将随 S 单调递增。

在 IBM 问题中，σ (SP , SN ) 随 SP 单调递增。这意味着当新的种子被添加到正种子集SP 时，不会导致阻塞集IBS(SP , SN )的大小减小。

2.2.2. Submodularity

定义 5. 子模性：设 f (S) 是集合的单调递增函数。令 S 和 T 为两个集合，使得 S ⊆ T ⊆ V 。如果满足以下等式，则函数 f (S) 是 S 的子模函数。

在 IBM 问题中，子模性是当向集合 SP 添加新的正种子节点时，σ (SP , SN ) 的边际增益递减的属性。也就是说，对于任意节点 v ∈ V \(SP ∪ SN )，将 v 添加到集合 SP ∪ {v} 中的边际增益小于或等于 SP 的增益。

为了解决 IBM 问题，贪心法采用蒙特卡罗模拟来计算网络中每个候选种子节点的边际增益 v / ε (SP ∪ SN )。贪心法的每一步都会选择边际增益最大的节点u加入SP作为新的种子节点：

3. Diffusion models

最近，网络科学、计算机科学和流行病学等领域报道了大量关于设计扩散模型的文献。我们将当前的影响力传播模型分为三大类：基于独立级联的扩散模型、基于线性阈值的扩散模型和基于流行病的扩散模型，在本节中，我们将回顾其中一些常见模型。

3.1. Independent cascade diffusion models

为了研究想法在社交网络上传播的方式，Kempe 等人。 [25]基于概率论中相互作用粒子系统的分析提出了独立级联（IC）模型。表1总结了基于独立级联的扩散模型的理论分析。在表的第 2 列中，我们显示了模型中节点的可能状态。第 3 列描述了模型的特征。

(1) Classical Independent Cascade Model

在经典IC模型下，每次影响力传播时，每个节点都处于活跃或不活跃状态。受影响的节点处于活动状态，不受影响的节点处于非活动状态。初始时，所有影响源节点都处于活跃状态。如果节点 u 在步骤 t 受到影响，它会在步骤 t + 1 尝试影响其不活动的邻居 v。节点 v 是否会受到其邻居 u 的影响将独立于 u 对其他节点的影响结果。此外，该模型假设每个受影响的节点 u 只有一次机会影响其邻居节点。无论成功与否，你都将不再有机会影响其邻国。当没有更多的节点可以受到影响时，这种影响传播的过程就结束了。此时，受影响节点的集合就是源的影响范围。经典 IC 模型以离散时间步长运行，如下所示：

(a) 在时间步 t = 0 时，集合 S 中的所有种子节点都处于活动状态，V\S 中的所有其他节点都处于非活动状态。

(b) 如果节点 u 在时间 t 被激活，它将尝试以概率 pu,v 激活其未激活的邻居节点 v。如果节点 v 被成功激活，则节点 v 在时间 t + 1 处转入激活状态。

(c) 这种扩散过程结束，直到不再有节点可以被激活。基于这种经典的IC模型，针对不同类型的网络和应用，人们提出了许多扩展的IC模型。在这些扩展 IC 模型中，离散时间步骤 (a) 和 (c) 与经典 IC 模型中的离散时间步骤相同，而步骤 (b) 具有不同的操作。

(2) Competitive Independent Cascade Model

陈等人。 [26]将 IC 模型扩展到竞争性社交网络，其中正面和负面影响在网络中同时传播。他们提出了竞争独立级联（CIC）模型，其中每个节点都处于非活动、正激活或负激活状态。在时间步 t = 0 时，所有正（负）种子节点均处于正（负）活动状态，所有其他节点均处于非活动状态。在 CIC 模型下，在时间 t 受到正面（或负面）影响激活的节点 u 将尝试以概率 pP u,v （或 pN u,v）激活其未激活的邻居节点 v。如果节点 v 被成功激活，则节点 v 在 t + 1 时刻将处于正向（或负向）状态。如果节点 v 受到正向和负向影响同时激活，则节点 v 在 t 时刻将处于负向激活状态+ 1。

(3) Homogeneous Competitive Independent Cascade Model

陈等人。 [26]提出了同质竞争独立级联（HCIC），以简化 CIC 模型中的概率设置。 HCIC 模型假设正面和负面影响在社交网络中的每条边 (u, v) 上具有相同的传播概率 pu,v，即对于 eu,v ∈ E，pP u,v = pN u,v =浦河谷在每个时间步，每个节点都处于非活动、正激活或负激活状态。在时间步 t = 0 时，所有正（负）种子节点均处于正（负）活动状态，所有其他节点均处于非活动状态。在时间 t 受到正面（或负面）影响激活的节点 u 将尝试以概率 pu,v 激活其不活动的邻居节点 v。如果节点v被成功激活，那么节点v在t+1时刻将处于正向（或负向）激活状态。如果节点v同时受到正向和负向影响激活，则节点v在t+1时刻将处于负向激活状态t + 1。
(4) Peer-to-Peer Independent Cascade Model

童等人。 [27]扩展了IC模型并提出了点对点IC（PIC）模型，该模型假设有q个级联C1，C2，…。。。，网络中的Cq。第 i 个级联 Ci 由其自己的种子集 Si 生成。此外，还存在由负种子集 SN 生成的负级联 CN 。在每个时间步，每个节点都处于以下状态之一：非活动状态、第 i 个正激活状态（i = 1, 2, ..., q）或负激活状态。在时间步 t = 0 时，所有第 i 个正（负）种子节点均处于第 i 个正（负）活动状态，所有其他节点均处于非活动状态。在PIC模型下，在时间t处于第i个正（负）活动状态的节点u将随机选择一个不活动的邻居节点v来以概率pu,v激活它。如果节点 v 被成功激活，它将在 t + 1 时刻转入第 i 个正（负）激活状态。如果节点 v 被两个或多个不同激活状态的邻居成功激活，则它将处于激活状态最高优先级级联在时间 t + 1 处获得最高优先级。

(5) Multi-Campaign Independent Cascade Model

布达克等人。 [6]还考虑到社交网络中可能存在同时传播的积极和消极影响，并在经典IC模型的基础上提出了多活动独立级联模型（MCICM）。该模型假设，虽然负面影响开始从网络中的一个节点传播，但正面影响也可以传播到网络的其他地方，并抵消负面影响的影响。在每个时间步，每个节点都处于非活动、正激活或负激活状态。在时间步 t = 0 时，所有正（负）种子节点均处于正（负）活动状态，所有其他节点均处于非活动状态。在 MCICM 模型中的每个时间步，每个节点都处于非活动、正激活或负激活状态。在时间 t 受到正面（或负面）影响激活的节点 u 将尝试以概率 pP u,v （或 pN u,v）激活其不活动的邻居节点 v。如果节点v被成功激活，则节点v将在t+1时刻变为正值（或负值）。如果两个或多个节点同时尝试激活节点v，则最多有一个节点可以成功激活它。只要该节点被激活，其状态就不再改变。
(6) Campaign-Oblivious Independent Cascade Model
Budak 等人基于 MCICM 模型。 [6]提出了Campaign-Oblivious Independent Cascade Model (COICM)，其中正面和负面影响通过每条边传播的概率相同。对于到达节点 u 的正面和负面影响，节点 u 以概率 pu,v 激活其邻居节点 v。在每个时间步，每个节点都处于非活动、正激活或负激活状态。在时间步 t = 0 时，所有正（负）种子节点均处于正（负）活动状态，所有其他节点均处于非活动状态。在时间 t 受到正面（或负面）影响激活的节点 u 将尝试以概率 pu,v 激活其不活动的邻居节点 v。如果节点v被成功激活，则节点v将在t+1时刻变为正值（或负值）。如果两个或多个节点同时尝试激活节点v，则最多有一个节点可以成功激活它。只要该节点 v 被激活，它的状态就不再改变。

(7) Temporal Campaign-Oblivious Independent Cascade Model

马努切里等人。 [28]引入了社交网络中的节点登录因素，并提出了Temporal CampaignOblivious独立级联模型（TCO-ICM）。 TCO-ICM将节点在每个时刻的登录概率login(v) ∈ [0, 1]添加到COICM模型中。在TCO-ICM中，每个节点只有在登录后才能激活其邻居节点。在每个时间步，每个节点都处于非激活、正激活或负激活状态。在时间步 t = 0 时，所有正（负）种子节点均处于正（负）活动状态，所有其他节点均处于非活动状态。在时间 t 受到正面（或负面）影响激活的节点 u 将尝试以登录（u）× pu,v 的概率激活其不活动的邻居节点 v。如果节点 v 被成功激活，则节点 v 将在 t + 1 时刻变为正值（或负值）。如果节点 v 被正负影响同时激活，则节点 v 将在 t + 1 时刻变为正值。

(8) Independent Cascade Diffusion Model in Signed Network

刘等人。 [29]提出了符号网络中的独立级联扩散模型（SNIC），以描述符号网络中两种影响的传播。签名网络中的节点具有三种状态：非活动状态、正激活状态和负激活状态。在带符号的网络中，每条边都有一个正号“+”或一个负号“-”。带有正号的边意味着它所连接的节点具有正向关系，例如朋友或伙伴。带有负号的边意味着它所连接的节点具有负面关系，例如竞争对手或敌人。假设边 eu,v 具有符号“+”，并且节点 u 在时间 t 被正（或负）激活，它将尝试以概率 pu,v 激活其不活动的邻居节点 v。如果节点 v 被成功激活，则节点 v 在时间步 t + 1 内将处于正（或负）激活状态。假设边 eu,v 的符号为“-”，节点 u 为正（或负）激活状态节点 v 在时间 t 被激活，如果它的非活动邻居节点 v 被成功激活，则节点 v 在时间 t + 1 时将处于负（或正）激活状态。如果节点 v 在同时，节点 v 将在时间 t + 1 时随机转变为正激活状态或负激活状态。

(9) Time-dependent Comprehensive Cascade Model

考虑到社交网络中信息传播的动态性质，Hao 等人。 [30]在经典IC模型的基础上提出了时间相关综合级联（TCC）模型。 TCC模型假设网络是动态的，并将网络划分为T个离散时间戳。 t 时刻的网络表示为 Gt = (Vt , Et ), t ∈ {1, . 。。 , T }，其中每个时间戳 t 中的单个 ut 只能以 Put ,vt 的概率尝试激活处于非活动状态的邻居 vt 一次。 TCC模型根据t时刻之前的历史活动来设置节点u激活节点v的概率。

在这里，|V|是网络中节点的数量，K 是状态变化率的可调参数，|St |是到时间 t 为止未能激活节点 v 的节点数量，fut ,vt 是节点 u 在时间 t 对 v 的影响。

3.2. Linear threshold diffusion models

在IC模型中，不活跃节点是否被激活取决于特定的邻居，而不是由其所有邻居的共同影响来激活。在现实世界的应用中，如果大多数人周围有更多接受某种观点的邻居，他们就更有可能接受某种观点。一个人对某种观点的接受可以被描述为社交网络中节点的激活，并且一个节点被激活的趋势随着更多其邻近节点被激活而单调增加。也就是说，随着时间的推移，如果越来越多的节点u的邻居被激活，则节点u更有可能被激活。线性阈值模型（LT）被提出来精确模拟这种现象。在线性阈值（LT）模型中，网络中的不同节点有不同的激活阈值。其他模型，例如IC模型，没有这样的激活每个节点的阈值，它们隐含地假设所有节点具有相同的激活阈值。因此，LT模型能够更准确地反映社交网络中传播影响力下节点的状态。 LT模型的另一个优点是，一个节点是否被激活并不取决于一个邻居的影响，而是取决于其所有邻居的综合影响。在其他模型中，例如 IC 模型，节点仅由其邻居之一激活，而不是由其所有邻居的联合效应激活。表2总结了线性阈值模型的理论分析。在表的第2列中，我们分析了模型中节点的可能状态。第 3 列描述了模型的特征。

(1) Classical Linear Threshold Model

肯佩等人。 [25]提出了线性阈值（LT）模型。 LT 模型的主要思想是，如果一个不活动的节点有足够数量的邻居处于活动状态，则该节点可以被激活。具体来说，图 G 中的每个有向边 eu,v 有权重 bu,v ≤ 1。他们用 Nin(v) 表示节点 v 的近邻集合。每条边 (u, v) 上的权重 bu,v 满足 Σ u∈Nin(v) bu， v ≤ 1。在每个时间步，每个节点都处于非活动或激活状态。此外，每个节点 v 都有一个阈值 θv ∈ [0, 1] 指示其对信息的接受程度。设 St 为 t 时刻激活节点的集合，当满足 Σ u∈Nin(v)∩St bu,v ≥ θv 时，非激活节点被激活。只要该节点被激活，其状态就不再改变。

经典 LT 模型以离散时间步长运行，如下所示：

(a) 在时间步长 t = 0 时，令 S0 为种子节点集。 S0 中的节点处于活动状态，所有其他节点处于非活动状态（种子集）。

(b) 在时间步长 t ≥ 1 时，令 St−1 为在时间步长 t − 1 之前或在时间步长 t − 1 时激活的节点的集合。如果满足以下条件，则非活动节点 v 将被激活： Σ u∈Nin(v)∩St−1 bu,v ≥ θv 。

(2) Competitive Linear Threshold Model

他等人。文献[5]在经典LT模型的基础上提出了竞争线性阈值（CLT）模型，该模型假设正向和负向影响可以同时在网络中传播，并且正向影响可以抵消负向影响。在CLT模型中，节点具有三种状态：非活动状态、正激活状态和负激活状态。 CLT模型中的每个节点v都有一个正激活阈值θ p v 和负激活阈值θ n v ，分别代表节点对正信息和负信息的接受阈值，θ p v 和θ n v 是从[0 ,1]。每个有向边 eu,v 还具有权重 bp u,v 和权重 bn u,v，分别表示边 eu,v 传播正向影响和负向影响的概率。在时间步 t ≥ 1 时，如果不活动节点 v 满足 Σ u∈Nin(v)∩Sn bn u,v ≥ θ n v ，则该节点 v 将被负激活。如果节点 v 满足 Σ u∈Nin(v)∩SP bp u,v ≥ θ p v ，则节点 v 将被积极激活。这里，SN和SP分别是当前正向激活和负向激活的节点的集合。如果节点v同时满足正激活和负激活条件，则节点v被负激活。在时间 t 负（正）激活的节点加入集合 SN（SP ），并保持负（正）激活状态。

(3) Competitive Activation Model

基于经典的 CLT 模型，Zhang 等人。 [31]提出了竞争激活（CA）模型，考虑到社交网络中的不同用户往往有不同的受到负面影响的概率。 CA模型引入了偏好参数Pf i v来确定节点v被激活的具体影响。该偏好参数定义为 Pf i v= ( Σ u∈Nin(v)∩S bn u,v ) /θ i v, i ∈ {P, N}。在CA模型中，节点具有三种状态：不活动状态、正激活状态和负激活状态。在时间步 t = 0 时，正（负）种子集 SP (SN ) 中的节点处于正（负）激活状态。所有其他节点均处于非活动状态。在时间步 t ≥ 1 时，如果满足 Σ u∈Nin(v)∩Sp bp u,v ≥ θ p v ，则失活节点 v 将被主动激活。如果节点 v 满足 Σ u∈Nin(v)∩Sn bn u,v ≥ θ n v ，那么它将被负激活。当节点v同时满足正激活和负激活条件时，如果Pf P v ≥ Pf N v则节点v被正激活，反之亦然。正（负）激活的节点加入集合 SP（SN ），并将对其邻居节点产生正（负）影响。

(4) Linear Threshold Model with One Direction State Transition

杨等人。 [8]提出了具有单向状态转移的线性阈值模型（LT1DT），用于对同一网络中的两种竞争影响传播进行建模。该模型考虑到用户接受真相的概率会随着许多复杂的社会因素而变化，并且用户被负面消息激活的状态可能会发生逆转。因此，为每个节点设置影响阈值和决策阈值，影响阈值和决策阈值在激活不活跃节点或说服激活的消极节点将其信念转变为事实时的不同阶段生效。在 LT1DT 模型中，每个节点在每一步都有三种可选状态：非活动状态、正激活状态或负激活状态。在每个时间步，每个节点都使用自己的节点级自动机来决定它转换到哪个状态。节点的状态转换取决于其当前状态及其受到的影响。除了对未激活节点进行激活过程外，同时对消极激活节点进行重新考虑过程。

(5) Multiple Topics Linear Threshold Model

范等人。 [32]研究了社交网络中多种类型信息的同时传播，并在经典LT模型的基础上提出了多主题线性阈值（MT-LT）模型。 MT-LT模型包含多个不冲突的信息源，因此MT-LT模型中的节点可以同时具有多个状态。例如，MT-LT模型假设有q个政治、经济、体育等主题，Si是主题i激活的节点集合。由于每个节点可以被不同的主题激活多次，因此节点的状态由集合 Q = {inactive, active1, active2,... 表示。。。 , 活跃q }。如果节点u没有被任何topic激活，则处于inactive状态；如果u已被主题i激活，则处于activei状态。如果节点u已被主题i和k激活，则其状态处于activei和activek。不同的节点对不同的主题有不同的接受度，因此节点 u 被分配一组激活阈值 θu = {θ 1 u , θ2 u ,...。。。 , θq u }，其中 θ i u ∈ [0, 1]。 θ i u 表示节点 u 对主题 i 的激活阈值。他们认为节点u对节点v的影响不仅与边权值bu,v有关，还与节点u本身对于不同主题的传播能量有关。因此，每个节点 u 也被分配一个向量 Pu = {p1 u, p2 u,...。。。 , pq u }，其中 pi u ∈ [0, 1] 表示主题 i 对其邻居节点的影响。令Si为处于activei状态的节点的集合。在每个时间步，当前未被 Si 激活的节点 u 如果满足： Σ u∈Nin(v)∩Si bu,v × pi u ≥ θi v，则将变为激活 i。

(6) Weight-Proportional Competitive Linear Threshold Model

鲍罗丁等人。 [33,34]考虑到网络中影响力传播存在竞争，节点的激活需要考虑两个竞争方，提出了权重比例竞争线性阈值（WPCLT）模型。 WPCLT模型假设网络中存在两种类型的影响力，并且它们彼此之间处于竞争关系。设 Si 为 i 类影响力 (i = 1, 2) 激活的节点集合，并令 S = S1 ∪ S2。 WPCLT模型中的节点存在三种状态：未激活、受影响和激活。节点可以通过两种方式受到 S1 或 S2 的影响而激活。设节点 v 的激活阈值为 θv，Ai t−1 为 t − 1 时刻之前第 i 类影响力（i = 1, 2）激活的节点集合，At−1 为激活的节点集合在时刻 t − 1 之前。在每个时间步，如果不活动节点 v 满足 Σ u∈Nin(v)∩S bu,v ≥ θv，则将其转换为受影响状态。然后，受影响的节点 v 将被第 i 类 (i = 1, 2) 影响激活，概率为 Σ u∈Ai t−1 bu,v / Σ u∈At−1 bu,v 。

(7) K -Linear Threshold Model

卢等人。 [34]考虑了社交网络影响力传播的多元竞争性，在经典LT模型的基础上提出了K线性阈值（K -LT）模型。 K-LT模型将影响力分为K类，节点的激活状态也分为K类。这样，影响力传播过程中的不活跃节点可以同时受到不同类别的活跃节点的影响。与WPCLT模型类似，K-LT模型中的节点具有三种状态，并且可以通过K种方式激活。令 Ai t−1 为在时间 t − 1 结束时受 i 类影响激活的节点集合，At−1 为在时间 t − 1 结束时激活的节点集合。时间步长，如果满足条件 Σ u∈Nin(v)∩S bu,v ≥ θv，则非活动节点 v 转变为受影响状态。然后，受影响的节点 v 将被第 i 类影响激活，概率为 Σ u∈Ai t −1 \Ai t−2 bu,v / Σ u∈At−1\At−2 bu,v 。

(8) Dynamic Linear Threshold

李等人。 [35]提出了一种动态线性阈值（DLT）模型，考虑到随着时间的推移同时传播和演化的竞争思想。他们估计用户u对邻居v的影响不仅基于两个节点之间的边权重，还基于时间范围。他们假设存在一个邻居最有可能受到影响的时间窗口。此外，与经典的LT模型不同，DLT模型允许用户根据邻居的影响改变他们之前的想法。具体来说，放弃rv表示用户v对放弃已经采纳的观点（可信的或错误信息）的怀疑，并且它随着时间的推移动态更新。表现出高度放弃的用户在采用和传播信息时持怀疑态度，而放弃率低的用户则不太不愿意。在时间步 t，每个受到负面或正面影响的用户 u 以概率 IF (v|t) 影响其不活动的邻居 v，该概率是基于边缘的权重和时间窗口 t 估计的。用户 v 根据其邻居的影响而采取信念。如果负面/正面影响超过放弃阈值rv，则用户v被感染。如果正面影响和负面影响都超过放弃阈值，则节点的状态不会改变。受到负面影响或正面影响的用户将被添加到可信组或受感染组中，并且放弃阈值 rv 会被更新。

3.3. Diffusion models based on epidemic

流行病模型是对传染病或病毒在人群中传播的研究。人们发现传染病的传播更类似于网络中影响力的传播，因此现在也扩展到对信息和影响力的传播进行建模。经典流行病模型根据节点的状态对节点进行分类，如易感（S）、感染（I）、康复（R）等，然后根据可行的状态转移定义不同的模型。在这篇综述中，我们将基于流行病的传播模型分为基于三态的影响力传播模型（示意图如图2所示）、基于四态的传播模型（示意图如图3所示）和基于四态的影响传播模型。基于节点状态数量的基于多状态的传播模型（示意图如图4所示））。

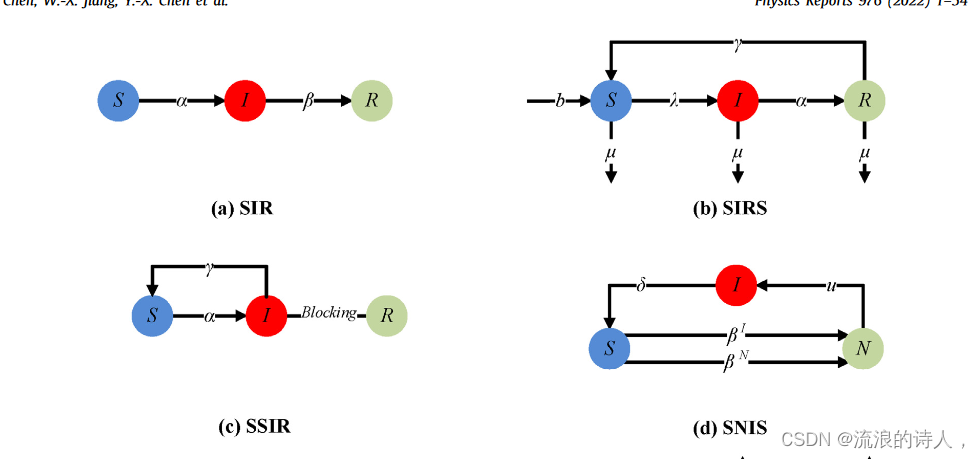
3.3.1. Three states epidemical models

(1) Classical Susceptible–Infected–Recovered Model

1927 年，Kermack 等人。 [36]首先应用流行病学模型来研究传染病的传播，并开发了易感-感染-康复（SIR）流行病学区室模型。 SIR传播模型将节点分为三种状态（如图2（a）所示）：易感者（S），易受病毒感染；感染者（I），接触病毒后被感染并传播；康复者 (R) 已从感染中康复。 SIR模型的传播规则如下：

(1) 被感染节点以概率 α 尝试感染处于易感状态 S 的节点，被感染的易感节点的状态由 S 变为被感染状态 I。

(2) 被感染节点的状态由 I 变为恢复状态R与恢复率β。

(2) Susceptible–Infected–Recovered–Susceptible Model with Birth and Death Rates

李等人。 [37]提出了一种具有出生率和死亡率的易感-感染-恢复-易感（SIRS）流行病模型来研究复杂异构网络中的病毒传播。该模型中，节点状态主要分为易感（S）、感染（I）和康复（R），其中自然出生和死亡与节点密度成正比，出生率b > 0，死亡率μ > 0（如图2（b）所示）。 SIRS模型的传播规则如下：

(1) 易感节点以概率 λ 转变为感染状态 I，并以概率 b 产生出生率，以概率 μ 产生死亡率。

(2) 感染节点以概率α转移到恢复状态R，且自身存在概率μ的死亡率。

(3) 恢复节点以概率γ转移到易感S，并以概率μ发生死亡率。

(3) Supervising–Susceptible–Infected–Recovered Model

谭等人。 [38]通过考虑信息传播过程中的人为干预因素改进了经典的SIR模型，提出了监督-易感-感染-康复（SSIR）模型。他们认为被感染的节点可以通过自我修复变回易受影响的状态，而传播者将完全失去传播信息的能力，然后通过人为干预改变到恢复的节点。该模型将节点的状态分为三类（如图2（c）所示）：易感（S）、感染（I）和恢复（R）。 SSIR模型的传播规则如下：

(1) 当易感节点暴露于感染节点时，它会以概率α转变为感染节点。

(2) 被感染的节点会以自愈率γ变回易感节点。

(3)被感染的节点受到随机的人为干预。一旦被感染的节点被人为干预，该节点就会转变为恢复节点。

(4) Incubation Epidemic Spreading Model with Continuous Detection

于等人。 [39]提出了一种具有传染性潜伏期的新型易感者-感染者-易感流行病（SNIS）模型。该模型在有向网络和异构网络上使用 N 交织平均场近似。该模型主要考虑传染病潜伏期对病毒传播的影响，即节点不具有传染性最初是在接触疾病后。但随着时间的推移，节点会变得具有传染性。他们将节点分为三种主要状态（如图2（d）所示）：易感（S）、传染性孵化但传染性（N）和感染（I）。

SNIS模型的传播规则如下：

(1)易感个体可能被感染者或暴露者感染，感染率分别为βI或βN。

(2) 状态N的个体在一段时间后以概率u转变为感染状态I。

(3) 感染者将以概率 δ 被治愈并转变为易感状态 S。

(5) Unknown–Dissemination–Immune Model

张等人。 [40]考虑了耦合社交网络中信息的扩散效应，在经典SIR模型的基础上提出了SI3R模型。 SI3R模型添加了独立和跨网络传播者两种新型节点状态，以增强信息传播。他们将节点分为三种主要状态（如图2（e）所示）：未暴露于舆论的未知节点（S）、传播节点包括网络中的节点。子状态独立传播（I1）、网内传播（I2）和跨网传播（I3），以及现在对任何舆情内容不感兴趣或传播信息后免疫的节点（R）

SI3R模型的传播规则如下：

(1) 对于不感兴趣的信息，未知个体将以概率α3变为免疫状态R。

(2) 未知个体将以转移概率α1成为独立传播状态节点I1。处于状态 I1 的节点会将信息传播到网络中的邻居。未知个体将成为网络间传播节点I2，转移概率为α2。处于状态 I2 的节点不仅对其网络中的影响感兴趣，而且还具有向其他耦合网络传播信息的能力。

(3) 跨网传播节点I2将以传播概率β转变为跨网传播节点状态I3。

(4) 随着时间的推移，具有不同状态 I1、I2 和 I3 的节点将分别以概率 λ1、λ2 和 λ3 变为免疫状态 R。

(6) 2Spreaders–Ignorant–Stifler Model

王等人。 [41]考虑到同构网络中存在两个及以上负面影响的异花授粉，提出了2SI2R影响传播模型。他们假设网络中传播着两种负面影响，称为谣言1和谣言2。此外，他们将节点分为三种状态（如图2（f）所示）：无知（I），没有听说过谣言，容易被谣言告知；传播者（包括传播者1（S1）和吊具 2 (S2)) 和节流器（包括节流器 1 (R1) 和节流器 2 (R2)）。其中，S1和S2分别是传播Rumor1和Rumor2的个体的集合。 R1 和 R2 分别是听过谣言 1 和谣言 2 但不会再传播的个体的集合。 2SI2R模型的传播规则如下：

(1) 当无知的个体接触负面影响传播者 S1 和 S2 时，其成为负面影响传播者的概率分别为 λ1 和 λ2。 (2) 当一个吊具与另一个吊具接触时，前者会成为抑制器。同时，当吊具与节流器接触时，吊具以α + δ 的概率成为节流器。 (3) 所有节点将以概率 g 自主退出网络。 (4) 如果传播器S2的传播能力比传播器S1强，则传播器S1与传播器S2接触时，会以概率β变为传播器S2；当节流器 R1 与吊具 S2 接触时，将以概率 γ 切换到吊具 S2 。

(7) Spreader–Ignorant–Stifler1–Stifler2 Model

王等人。 [42]开发了一种称为传播者-无知-Stifler1-Stifler2（SIRaRu）的新传播模型，其中当无知的个体接触到负面信息时，他或她要么受到其影响而成为传播者，要么转变为传播者，并且不再传播负面信息。该模型还采用了遗忘机制，并假设传播者能够以一定的概率转化为负面信息的抑制者。他们将节点分为三种主要状态（如图2（g）所示）：无知（I），传播者（S），停滞者（stifler1（Ra）和stifler2（Ru））。其中Ra是接受负面信息但不传播的人，Ru是不接受负面信息的人。 SIRaRu模型的传播规则如下：

(1) 一个无知个体在状态 S 下成为传播者的概率为 λ，在状态 Ra 下成为传播者 1 的概率为 γ；或者在状态 Ru 下成为 stifler2 的概率 β，其中 λ + β + γ = 1。 (2) 传播个体在暴露于传播者、stifler1 或 stifler2 后，将以概率 α 转变为状态 Ra 中的 stifler1。另外，模型中存在遗忘机制，传播者会以概率 δ 直接转变为 Ra 状态下的 stifler1。

(8) Spreading Model Considering the Public Opinion Environmental Factor

潘等人。 [43]设计了影响力传播模型（S2IM），该模型考虑了有利于传播的舆论环境。该模型将节点分为三类：确信个体（I1）、客观个体（I2）和未知个体（S）。模型中加入了舆论环境因子M，它会同时受到I1和I2的影响。此外，该模型还具有I1、I2和M的衰减衰减，衰减率分别为u、v和k（如图2（h）所示）。 S2IM模型的传播规则如下：

(1) 当未知节点与确信节点接触时，未知节点会以概率 a 转变为确信状态 I1，并且在转变过程中会受到观点环境因子 M 的影响。

(2)当未知节点与客观节点接触时，未知节点将以概率b转变为客观状态I2，并且在转变过程中不会受到舆论环境因素M的影响。

(3) 确信节点和客观节点将分别以衰减率 u 和 v 转变为未知状态 S。

(4) 当目标节点与确信节点接触时，目标节点将以概率 c 转变为确信状态 I1。

(5) 舆论环境影响的程度会受到确信节点和客观节点的影响，概率分别为r1和r2。而且舆论环境的影响程度也会以概率k下降。

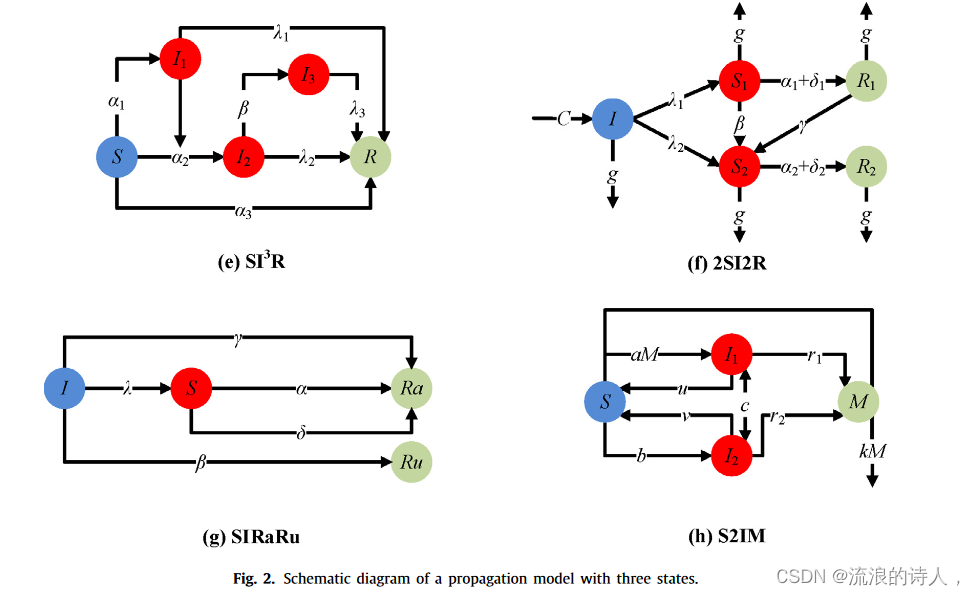
3.3.2. Four states epidemical models

(1) Susceptible–Exposed–Infected–Removed Model

在现实网络中，个体由于自身特点或社会因素，在接触到负面信息时，会处于优柔寡断的状态，因为他们不确定信息是否正确。因此，它们有可能变成感染节点或者变成不受影响的节点。基于此，刘等人。 [44]提出了一种新的易感-暴露-感染-移除（SEIR）影响传播模型，将节点分为四类（如图3（a）所示）：易感（S）是那些尚未感染的节点信息中，暴露（E）的是那些已经被感染，但不散布谣言的人，被感染（I），被移除（R）。

SEIR模型的传播规则如下：

（1）易感个体在与感染节点接触后，将以概率λ转变为暴露状态E。

(2) 暴露个体以β(1−h)的概率被治愈，并转变为去除状态R。也可能以βh的概率转变为感染状态I。

(3) 被感染个体将以概率 δ(1 − m) 被治愈并转变为移除状态 R。它也将以概率 δm 重新转移回暴露状态 E。

(2) Improve Susceptible–Infected–Quarantined–Recovered Model

在实际网络中，往往会因病毒等负面影响的突然爆发而导致隔离措施滞后，导致隔离效果不佳。为了解决这个问题，Li 等人。 [45]在SIQR模型[46]的基础上考虑无效隔离因素，开发了一种改进易感-感染-隔离-恢复（Improve-SIQR）模型，该模型具有新的加入率和非自愿退出率。该模型将节点分为四类（如图3（b）所示）：易感（S）、感染（I）、隔离（Q）和恢复（R）。

Improve-SIQR模型的传播规则如下：

(1)可以将节点以新加入率b加入到易受影响的节点集合中。易受影响的节点可以以概率 d 自主退出该状态。易受影响的节点可以以概率 m 转换为隔离节点。一些易感节点可能会因传播率λ和接触率β的影响而转变为感染节点。

(2) 感染节点可以以概率 p 自主退出状态，并以概率 α 转变为隔离状态 Q。

(3) 隔离节点无法转变为恢复节点并退出的概率为γ，隔离节点成功转变为恢复状态R的概率为μ。每个被隔离节点自主退出网络的概率为δ。

(4) 隔离节点转变为恢复状态R后，不会再被感染，恢复的节点也会以概率δ自主退出网络。

(3) Susceptible–Infective–Counterattack–Refractory Model

赞等人。 [47]考虑了反击机制对负面信息传播的影响，提出了易感-感染-反击-难治（SICR）模型。该模型在经典SIR模型的基础上增加了一类反攻击者节点来反驳负面信息。 SICR模型将节点分为四类（如图3（c）所示）：易感性（S）、感染性（I）、反击性（C）和难治性（R）。其中，顽固节点是那些听到谣言但失去传播谣言兴趣的人。一旦节点转变为反击状态，该节点的状态将不会再次改变，直到传播结束。

SICR模型的传播规则如下：

(1)当易感节点接触感染节点时，易感节点可能会出现三种结果：以概率α成为感染节点；成为难熔节点的概率为β；成为反击节点的概率为 θ 。我们假设状态 C 是一个常量状态，即一旦节点变为状态 C ，它将保持状态 C 直到结束，这与状态 R 类似。

(2) 当一个感染节点接触另一个感染节点或难治节点时，它以概率 γ 变为难治状态 R 。

(3) 如果反击节点有感染性邻居节点，则感染性邻居以概率 η 变为难治状态 R。

(4) Credulous–Spreader–Rumor Killer–Recovery Model

李等人。 [48]提出了一种Credulous-Spreader-Rumor Killer-Recovery（CSER）影响力传播模型，考虑到网络中存在一些类似于警察的节点，通过某种策略控制负面信息的传播。该模型将节点分为四类（如图3（d）所示）：轻信者（C）、传播者（S）、谣言杀手（E）和理性者（R）。 CSER模型的传播规则如下：

(1) 当轻信个体接触传播者时，轻信个体将以概率 λ 转变为传播状态 S。同时，如果轻信的个体对负面信息不感兴趣，他/她将以概率β转变为理性状态R。

（2）当传播者在传播负面影响的过程中接触到谣言杀手时，就会以概率α转变为谣言杀手状态E，并积极尝试阻止负面信息的进一步传播。

(3)如果传播者在传播过程中对负面信息失去兴趣，就会以概率δ转变为理性状态R。此外，当一个传播者与其他传播者、谣言杀手或理性者进行交流时，他们会以概率 σ 转化为理性状态 R 。

(5) Susceptible–Infected–Hibernator–Removed Model

赵等人。 [49]考虑了遗忘和记忆机制对影响传播的影响，在经典SIR模型的基础上提出了易感-感染-冬眠者-移除模型（SIHR）模型。 SIHR模型将节点分为四类（如图3（e）所示）：易感者（S）、感染者（I）、冬眠者（H）和移除者（R）。该模型添加了从易感性到恢复状态的直接联系。还添加了一组新的冬眠者来体现遗忘和记忆机制。 SIHR模型的传播规则如下：

(1) 当易感节点与感染节点接触时，易感节点将分别以概率 λ 和 β 转变为感染状态 I 和恢复状态 R。

(2) 为了体现遗忘机制，受感染节点将以遗忘概率δ转变为休眠状态H。另外，为了体现记忆机制，冬眠节点会以自发记忆概率 ψ 转变为感染状态 I。如果休眠节点接触到传播节点，它将转变为感染状态 I，唤醒记忆率概率为 η。

(3)当一个感染节点与另一个感染节点、休眠节点或恢复节点接触时，它会以概率α转变为恢复状态R。

(6) Susceptible–Indifferent–Propagating–Recovery Model

朱等人。 [50]提出了基于沉默机制的敏感-无关-传播-恢复（SAIR）模型。该模型监控网络中的负面信息，进而防止某些节点受到负面信息的影响。该模型将节点分为四类（如图3（f）所示）：易受影响（S）、无关（A）、传播者（I）和恢复者（R）。冷漠的个体相信负面信息，但不传播它。 SAIR模型的传播规则如下：

(1) 新个体以概率 B 进入网络，处于网络不同状态的个体以相同的概率 μ 移出网络。

(2) 冷漠个体和扩散个体有自主恢复概率ρ。

(3)易感个体分别以概率θ1和θ2转移到无差异状态A和传播状态I。易受影响的个体以 1 − θ1 − θ2 的概率转移到恢复状态 R。另外，从传播个体到易感个体的传播率为φ。

(4) 受强制沉默策略影响的传播者将以 h 的概率进入冷漠状态 A。

(7) Ignorant–Weak spreader–Strong spreader–Removal Model

冉等人。 [51]提出了基于个体兴趣程度差异和虚假信息机制的无知-弱传播者-强传播者-移除（IWSR）模型。他们认为个体对同一信息有不同的兴趣，可以主动传播它，否则他们可能对该信息不感兴趣，成为弱传播者。该模型根据节点的通信方式将节点分为四种状态（如图3（g）所示）：无知（I）、弱传播者（W）、强传播者（S）和恢复（R）。

IWSR模型的传播规则如下：

（1）网络中的新个体以概率δ变得无知。

(2)强传播者在不同信息的影响下以概率β转变为弱传播者。

(3) 强传播者以概率 λ2 影响无知者成为强传播者；弱传播者以概率 λ1 影响无知者成为弱传播者。

(4) 传播者以概率 α 停止传播负面影响，进入状态 R。

(5) 处于网络不同状态的个体可能以概率 δ 移出网络

(8) Ignorant–Spreader–Recovery–Critical Model

王等人。 [52]观察到，一个人在多次受到负面信息的影响后，可能会成为负面影响传播者。他们提出了一种基于自进化机制的无知-传播-恢复-关键（ISRC）影响传播模型。该模型将节点分为四类（如图3（h）所示）：无知者（I）、传播者（S）、批评者（C）和恢复者（R）。 ISRC模型的传播规则如下：

（1）当无知的个体接触到传播者时，他们会以概率α变成传播者。同时，无知者具有自我净化机制，会以a2+b2的概率转变为批评状态C；无知者也会以a1+b1的概率改变到恢复状态R。

(2)批评者将以概率β改变到恢复状态R。但随着批评者接触到越来越多的负面信息，批评者将以概率a3转变为传播者状态S。

(3) 吊具将以θ + β 的概率改变到恢复状态R。

(9) Disseminate & Discriminate–Spread–Exposed–Ignorant–Recover Model

李等人。 [53]提出了一种基于用户传播能力和判别能力的动态信息传播模型，称为传播和辨别-传播-暴露无知-恢复（DDSEIR）。 DDSEIR模型将节点分为四类（如图3（i）所示）：ignorant（I）、expose（E）、spreader（S）和recover（R）。 DDSEIR模型的传播规则如下：

(1) 当无知节点与高级身份传播者接触时，将以概率 p 转变为暴露状态 E。类似地，当一个无知的节点与一个共同的身份传播者接触时，它会以 (1 − p)α 的概率转变为暴露状态 E。其中，p和1−p分别为高级用户和普通用户占用户总数的比例。 (2) 暴露节点会对接收到的信息进行识别，如果判断是否定的，则直接以概率 ω(1 − F ) 转变为恢复状态 R。如果结果不为负，则以概率 ωF 转变为扩散状态 S。 (3)如果传播者遇到了那些已经收到信息的人(E、R、S状态)，则它以概率α转入恢复状态R，因为用户评估该信息没有价值。在自卫机制下，传播者可能会忘记其传播信息的动机。如果信息伪装得很好，导致用户难以做出是否发送的决定，则传播者将以概率δm转入暴露状态E，并继续规则2）中的过程，否则将转入恢复状态 R 的概率为 δ(1−m)。

3.3.3. Multiple states epidemical models

(1) Ignorant–Latent–Spreader–Cooled–Removed Model

陈等人。 [54]提出了一种称为无知-潜在-传播-冷却-移除（ILSCR）的影响传播模型来控制紧急情况下的负面影响传播。该模型认为，传播者在成为窒息者之前可能会经历一段冷静期，而且人员流动主要集中在某一区域。 ILSCR模型将节点分为五类（如图4（a）所示）：无知者（I）对负面信息一无所知，潜伏者（L）在接触负面信息后无法立即做出决定，负面信息传播者（S）、通过本地信息确认负面信息捏造后停止向他人传播负面信息的冷酷者（C）、属于被剔除阶层的扼杀者（R）。 ILSCR模型的传播规则如下：

(1) 新个体可能以概率ε在网络中变得无知。不同状态节点以概率 ρ 从网络中移除。

(2)当无知者与潜在者或传播者接触时，无知者将分别以γ1或γ2的概率转变为潜在状态L。

(3) 潜在变量将以概率 α 转变为扩展器状态 S。

(4)负面影响传播较长时间后，传播者不再愿意相信负面信息，会以概率δ1转变为较冷状态C。另外，由于遗忘机制，传播器将以概率λ转变为恢复状态R。

(5) 当负面信息被证明错误后，冷却器将以δ2的概率转变为恢复状态R。

(2) Suspect–Dangerous–Infective–Latent–Recovered

姚等人。 [55]认为在社交网络中，易感节点在负面信息出现后立即成为感染节点是不合理的，因为负面信息传播到易感节点需要一定的时间。另外，由于传播者的顽固性，当负面信息被证明是虚假的时，他们会处于一种特殊的状态，可能传播负面信息，或者可能对负面信息免疫。基于这些因素，他们设计了一个可疑-危险-感染-潜伏-恢复（SDILR）模型来模拟影响的传播。该模型将节点分为六类（如图4（b）所示）：未接触过负面信息的易感者（S），有网友传播负面信息且面临迫在眉睫危险的危险者（D）。被欺骗、传染性（I）、传播负面信息、潜伏性（L）、传播负面信息但暂时停止传播、恢复性（R），SDILR模型的传播规则如下：

(1) 新个体以概率μ在网络中变得无知，并且不同状态节点以概率μ从网络中移除。

(2) 当易感节点与感染节点接触时，易感节点将以概率β转变为危险状态D。

(3) 危险节点以概率ρ转变为感染状态I。而且，它们可以以概率 δ 转变为恢复状态 R。

(4) 被感染的节点可能以概率 γ 转变为潜在状态 L 。同时，潜在节点可能以概率 θ 恢复到受感染状态 S 。

(5) 潜在节点可以以概率 φ 转变为恢复状态 R。

(3) Susceptible–Exposed–Trusted–Questioned–Recovered Model

张等人。 [56]提出了敏感-暴露-可信-质疑-恢复（SETQR）影响力传播模型，以确保模型与实际情况密切相关。该模型考虑了以下因素：受感染的节点可以选择性地传播信息；网络中的某些节点是免疫的；信息处理存在时间滞后；并且有可能免疫节点再次被激活。该模型将节点分为以下五类（如图4（c）所示）：易受影响（S）、暴露（E）、可信（T）、质疑（Q）和恢复（R）。其中，暴露节点是那些接收到信息但不确定信息是否被传播的节点。可信节点是那些相信接收到的信息并传播该信息的节点。被质疑的节点是那些不相信收到的信息但传播该信息的节点。

(4) Suspect–Exposed–Symptomatic–Infected–Asymptomatic–Infected–Recovered-Death Model

基于现有的流行病分区模型，Chen 等人。 [57]提出了考虑有症状和无症状感染者的实际传播路径的隔室动态模型（SEI1I2RD）。他们的结论是，病毒的传播潜伏期长、无症状感染者数量多。传播模型将节点分为五类（如图4（d）所示）：易感（S）、暴露（E）、感染（I）、恢复（R）和死亡（D）。其中，感染节点由有症状感染者（I1）和无症状感染者（I2）组成。 SEI1I2RD模型的传播规则如下：

(1) 当易感节点暴露于有症状的感染者 I1 时，将以概率 α 转变为暴露状态 E；或以概率 β 达到无症状感染状态 I2。 (2) 暴露的节点将以概率 σ 转变为有症状的感染状态 I1 。 (3) 有症状的感染节点将以概率 u 转变为死亡状态，或者以概率 γ1 转变为恢复状态 R。 (4) 无症状感染节点将以γ2的概率转变为恢复状态R。

3.4. Other types of diffusion models

除了上述常用的扩散模型外，最近文献报道了一些影响力扩散模型。范等人。 [58]介绍了机会性一激活一（OPOAO）和确定性一激活多（DOAM）模型。这两个模型都描述了网络中同时演化的两个级联的扩散。在 OPOAO 模型中，影响力传播过程类似于移动社交网络中人与人之间的联系机制，即每个人同时只能与一个人进行交流，而在该模型中，影响力传播速度较慢，原因是重复选择的存在。 DOAM影响力传播机制类似于信息广播过程，每一步，新激活的节点数量都会大幅增加，影响力传播的速度相比OPAO模型相当快。郭等人。 [59]提出了多特征扩散模型（MF模型），该模型假设信息具有多维特征，并且信息扩散过程不是简单的一维扩散，而是多维、逐个特征的扩散。尽管每个特征对于不同用户的重要性不同，但该模型通过平等对待这些特征来简化模型。范等人。 [60]基于IC和LT模型提出了两种模型来捕获竞争影响力扩散过程，即带有会议事件的谣言-保护者独立级联模型（RPICM）和带有会议事件的谣言-保护者线性阈值模型（RPLT-M）。在这两个模型中，存在两种类型的级联扩散：保护者和谣言。此外，这些模型还具有三个特征，包括时间期限、信息交换之间的随机时间延迟以及接受信息的个人兴趣。

王等人。 [61]在伊辛模型[62]的基础上提出了影响力扩散的动态模型，他们认为信息扩散的成功取决于话题的全球流行度和个体对信息的倾向，这可以看作是伊辛模型的概括特征。

4. Methods

近年来，文献报道了影响力阻断最大化方法。这些方法主要分为三类：基于中心性的方法、基于启发式的方法和基于社区检测的方法。除了回顾这三类主要方法之外，我们还回顾了一些解决具有一定约束的 IBM 问题的方法，例如成本约束 IBM 问题，它不仅考虑了抑制效应，还考虑了使用正种子的成本。另一个例子是IBM关于来源不确定的问题。该问题假设负信息的来源未知，我们只知道每个节点成为负种子源的概率。

4.1. Methods based on centrality

基于中心性测度的方法主要评估网络中节点和边的重要性，选择重要的节点或边来阻断或抑制负面影响。

4.1.1. Node centrality measurements

基萨克等人。 [14]认为网络的拓扑结构对节点的传播起着重要作用，最有效的传播者往往存在于网络的核心区域。因此，他们提出了k-shell分解方法来选择有影响力的节点。该方法中，k-壳分解的步骤如下：在第一步k-壳分解中，将度数k＝1的节点全部移除，这可能使得剩余的度数k≤1的节点出现。继续删除所有度数 k ≤ 1 的节点，直到所有剩余节点的度数 k > 1。所有删除节点的 k-shell 值设置为 1。第二步，删除所有度数 k = 2 的节点，直到所有节点剩余节点的度k > 2。将第二步中所有移除节点的k-shell值设置为2。对剩余节点重复此剪枝过程，直到所有节点被移除。最后，为每个节点分配一个 k-shell 值。实验结果表明，k-shell方法具有较强的鲁棒性，但在存在多个传播源且影响传播范围重叠的情况下，该方法的有效性值得怀疑。于等人。 [63]研究了几种结构措施来确定静态和动态社交网络中的最佳拦截器，并观察到它们的删除将大大降低网络中的交流程度。他们发现，对于静态和动态网络，简单的局部指标（例如节点度）是非常好的指标，并且可以作为出色的拦截器。马等人。 [64]发现，如果节点的邻居具有较高的k-shell值，则该节点的影响力较高[14,65]，并且节点之间的影响力随着距离的增加而减小。受引力公式思想的启发，他们提出了重心指数来衡量网络中节点的传播影响力。该方法将节点i的k壳值作为其质量，并将节点之间的距离定义为节点之间的最短路径。由此，网络G中节点i的影响力G(i)计算如下：

这里，dij是节点i和j之间的最短距离，ks(i)、ks(j)分别是节点i和j的k壳值。 ψi 是到节点 i 的最短路径不超过阈值 r 的节点集合。为了降低算法的计算复杂度，他们将r设置为3。因此，扩展重力指数的定义如下：

这里，Λi是节点i的最近邻集。实验结果表明，该方法比度中心性、介数中心性等指标更有效，在SIR模型中也取得了更好的效果。在一些在线消息社交网络中，人们更容易受到亲密朋友的影响，传统上认为一个节点拥有的朋友越多，即度越大，该节点在社交网络中的重要性就越高。然而，很多时候，人们的影响力不仅仅取决于好友的数量，还取决于好友的重要性，即好友越重要的节点，在信息传播中会发挥越重要的作用。姚等人。 [66]提出了一种基于特征向量中心性的算法，其中特征向量中心性的值用于衡量网络中节点的重要性，这也是社交网络中节点重要性的重要衡量标准。如果某个节点的特征向量中心性值较大，则可以表明该节点与特征向量中心性值较大的节点的联系更加紧密。令 c(vi) 为节点 vi 的特征向量中心性 (EVC)，定义为：

这里，A是社交网络图G的邻接矩阵，N(vi)是节点vi的邻居集，λ是给定的常数。设C = (c(v1), c(v2), ..., c(vn))T为图G中所有节点的中心向量，n为节点数，则式(1) (10) 可以转化为如下形式：

从等式可以看出。 (11) 根据Perron-Frobenius定理[67]，C是矩阵AT的最大特征值对应的特征向量，λ是矩阵AT的最大特征值。该算法选择负面种子节点的邻居集中EVC值最大的节点作为抑制节点，阻止负面影响的传播。

阿拉兹哈尼等人。 [68]研究了用户的社会地位对影响力封锁的影响，提出了Centrality_IBM算法，该算法使用三种不同的中心性策略，包括接近中心性、介数中心性和度中心性，找到k个正节点来阻止负面影响的传播。度中心性方法从所有非负种子节点中选择度数最大的节点作为候选正种子节点。紧密中心性方法通过计算该节点与图中所有其他节点之间的最短路径长度之和的倒数来对节点进行排序。节点介数中心性方法通过计算经过目标节点的所有节点之间的最短路径条数来衡量目标节点。在不同类型数据集上的实验结果表明，三种不同中心性度量的效果有所不同，但总体效果优于随机选择种子节点的方法。

王等人。 [69]提出了一种基于最大边际增益规则的贪心算法来寻找最优种子节点集来阻止负面影响的传播。实验发现，与基于中心性的出度、介数和PageRank方法相比，该算法取得了更好的性能。维贾延托等人。 [70]将图连接性与中心性结合起来作为一种称为保护度量的测量。他们提出了PowerShield方法来选择阳性种子。该方法中，连通性是通过图邻接矩阵的最大特征值对应的特征向量来衡量的。中心性准则是通过节点的度来衡量的，即具有更多邻居的节点被认为更重要。因此，节点i的Protection Metric可以通过式（1）计算： (12) 式中，ηi 为矩阵最大特征值对应的特征向量第 i 个元素，d(i) 为节点 i 的度数。

张等人。 [71]发现在一些在线社交网络如新浪微博中，有影响力的节点的出度通常远高于其入度。此外，他们认为我们不应该简单地选择最有影响力的节点来阻止负面影响，因为这可能会导致其追随者或其他用户的不满。他们基于信息熵理论，提出了一种利用用户容忍度的负面影响阻断方法的节点选择机制。该方法中，pin u和pout u分别为节点u的入度和出度的比例概率。

4.1.2. Edge centrality measurements

戴伊等人。 [74]观察到中心节点在信息传播中发挥着重要作用，但是封锁这些中心节点，例如中间性和接近中心性最高的节点，在影响力抑制方面并没有取得更好的效果，因为删除特定节点可能会导致增加另一个节点的重要性。基于对 Twitter 网络的观察，他们发现边介数方法优于一类基于节点中心性的方法[75]。卡里尔等人。 [76]提出了一种基于贪婪边缘删除的算法来解决谣言阻塞问题，即删除一组k条边缘，从而在LT模型下最小化谣言传播。他们表明，这种基于边缘删除的谣言阻止问题具有超模块化目标函数，因此可以通过具有可证明的近似保证的贪婪方法来解决。 Yao 等人的目标是阻止 k 个链接以最大程度地减少最终受感染的用户规模。 [77]提出了一种保证精度的贪心算法和两种基于介数和出度的有效启发式算法来寻找该问题的近似解，其中边e的介数b(e)计算为：

这里，N(u,v)是节点u和v之间的最短路径的数量，n(e;u,v)是节点u和v之间通过边e的最短路径的数量。如果 N(u, v) = 0，则 b(e) = 0。在两个真实网络上的实验结果表明，贪心算法在最小化负面影响方面更有效。但就运行时间而言，基于介数和出度的启发式算法比贪心算法快几个数量级。

阿莫鲁索等人。 [78]提出了一种启发式方法，在网络节点中放置多个监视器来控制可疑节点传播的信息，并在错误消息到达网络的大部分之前阻止错误消息对其余节点的影响。他们提出了切点的概念，切点是负面影响节点和单个目标节点之间的边。如果将剪切中的所有边都从网络中删除，则负面影响节点和目标节点之间将不存在可达路径。因此，如果将监视器放置在剪切的末尾，则可以在传播到目标节点之前阻止节点 s 的负面影响。

严等人。 [79]证明了从网络中移除某些边集以抑制负面影响传播的问题的目标函数不满足子模型，因此他们提出了一个子模下限界和目标函数的子模上限，并设计了一种启发式方法 MDS 来计算目标函数。该方法根据每个节点的边际减量来选择种子节点，可以通过从网络中去除边来准确计算种子节点。该问题的目标函数相当于最大化总边际减量。令 θE\{est }(v) 表示当边 est 从当前网络 E 中移除时，节点 v 被种子集 S 激活的概率。令 ΔεθE\ε(υ) 为移除后节点 v 的边际减量边集 ε，则总边际减量为：

严等人。 [80]提出了一种由生成候选集和选择阻塞阶段两个阶段组成的方法。第一阶段是寻找散射影响最大的前a×k节点作为候选集，其中a是阈值参数。该阶段可以有效减少后期贪心算法的时间消耗。第二阶段基于贪心策略，从候选集中选择k个节点来阻止负面影响的传播。为了选择候选集，应通过式（1）估计所有节点的负面影响传播能力。 (19) 式中，A为网络的邻接矩阵，I为单位列向量，r为传播路径的长度限制。 σ中各元素的值对应于相应节点的负面影响传播能力。

木村等人。文献[24]利用密钥渗流法的思想估计了节点 v ∈ V 的影响度 σ (v;G)，比传统的链接删除启发式算法有较大的性能提升。他们将图 G 边界处的渗透过程称为随机过程，其中信息以概率 pe (e ∈ E) 通过每条边 e 传播。给定一个正整数M，该方法执行M次边缘渗滤过程并构成M张图，用Gm=(V，Em)(m=1，...，M)表示。根据文献[81]，图上的概率问题可以映射为边界渗流过程。因此节点v的影响程度σ(v;G)可以用式(1)中的s(v;G,M)来近似。 (20)，其中F(v；Gm)是图Gm中从节点v可到达的所有节点的集合。

如果 M 很大，那么每个图都可以分解为强连通分量（SCC），如下所示：

4.2. Methods based on heuristic

启发式算法是指通过归纳推理和对过去经验的实验分析来解决问题的方法。启发式算法借助于某种直观的判断或试探性的方法，能够得到问题的次优解或以一定的概率找到其最优解。通用性、稳定性和更快的收敛速度是衡量启发式算法性能的主要标准。

4.2.1. Network sampling-based methods

陈等人。 [84]提出了度折扣启发式，并且还改进了其他级联模型中基于度的启发式。算法的思想是这样的：如果u是种子节点，那么它的邻居节点v的度应该打1。同样，如果v在种子节点集中有m个邻居节点，那么v的度应该折扣为 m。在IC模型中，当传播概率p较小时，该方法只关心v对其直接邻居的影响，而忽略节点v的多跳邻居。虽然该方法适用于大规模社交网络，其准确率不高，该方法在LT等其他模型中的有效性尚不清楚。陈等人。 [85]通过为每个节点构建局部树结构来对影响力传播进行建模，并设计了一种新的启发式算法，可以扩展到数百万个节点和边，该算法具有一个简单的可调参数，可供用户控制运行时间和影响力之间的平衡算法的范围。该算法首先使用 Dijkstra 的最短路径算法计算网络中节点对之间的最大影响路径 (MIP)。为了有效限制对局部区域的影响，可以忽略概率小于影响阈值θ的MIP。然后，在每个节点开始或结束的 MIP 被合并到表示每个节点的局部影响区域的树结构中。因此，只需要考虑通过这些局部树结构传播的节点的影响，作者将该模型称为最大影响树结构（MIA）模型。在基本的 MIA 模型中，如果从种子节点 sj 到节点 v 的 MIP 上存在一个种子节点 si，则 si 会阻挡 sj 对 v 的影响。因此，为了更好地模拟原图中的影响传播，作者提出了一种扩展前缀排除MIA（PMIA）模型来寻找从sj到v的路径中不存在节点si的替代路径。在扩展模型中，当选择下一个种子时，对于每个节点v，其在需要重新计算图表。最后，所有被选中的种子按照选择顺序形成一个序列S，并且S中的任意种子s都有到所有节点v的替代路径。因此，节点v的MIA结构由两部分组成，分别是并集PMIIA(v,到 v 的 MIP 的 θ ) 和从 v 到其他节点的最大影响路径的并集 PMIOA(v, θ )，其中 θ 是影响传播概率的阈值。该方法可扩展到数百万种大小的图表，并且在大多数情况下，它显着优于所有其他可扩展启发式方法，将影响范围增加 100% 至 260%。为了解决效率问题，He 等人。 [5]利用LT模型对有向无环图（DAG）的高效计算特性，针对CLT模型下的IBM问题设计了一种高效的启发式CLDAG。实验结果表明，CLDAG算法在阻塞效果上与贪婪算法相当，同时显着提高了运行时间。

李等人。 [86]设计了一种快速近似算法，使用2跳方法来模拟从节点开始的影响传播。然后，为了加速贪婪算法，他们提出了基于节点删除的启发式算法来检测最佳种子节点，以最大化负数上的阻塞。童等人。 [87]提出了一种基于反向元组的随机负面影响分块算法，该算法利用反向采样技术来获得IBM问题的目标函数的估计值。该方法中，节点v的随机反向元组TV=(V*,Et,Ef,B)构造如下：从节点v开始，采用广度优先搜索顺序检测其邻居是否可以添加到其可达节点集V*，直到负种子或没有节点可以进一步到达。其中 Et 和 Ef 是边集，B 是布尔变量。该算法在IC模型下具有良好的分块效果，但模型参数较多，难以优化。基于 MIA 结构，Chen 等人。 [88]设计了两种启发式CMIA-H和CMIA-O，分别在MCICM和COICM两种竞争传播模型下有效地解决IBM问题。实验结果表明，CMIA-H 和 CMIA-O 都实现了与贪婪算法相同的阻塞性能，并且始终优于其他基线启发式算法。 CMIA-H 和 CMIA-O 都比贪婪算法快几个数量级。为了计算被阻止的负面影响，CMIA-H利用正向传播的高效特性，可以轻松判断负面种子对其他节点的影响是否被完全阻止或不被阻止。 CMIA-O中的计算过程采用动态规划方法来高效计算每个节点的负激活概率，进而计算被阻止的负影响。尽管这两种算法对阻塞性能的影响与贪婪算法相似，但它们缺乏近似保证。林等人。 [89]提出了Block Influence Out Graph（BIOG）算法，通过使用新的图结构Maximum Influence Out-Graph（MIOG）来建模负面影响的传播区域，从而有效地阻止负面影响的传播。该算法计算网络中每个节点的全局阻塞分数，将分数最高的节点作为正向影响节点，然后更新负向影响节点的传播区域，直到负向影响被阻塞或满足终止条件。目前大多数算法都是基于一维扩散模型设计的。事实上，一个节点有多个特征，用户对每个节点的影响力不仅取决于其中一个特征，还取决于其对与该节点相关的所有特征的整体评价。因此，一个节点的影响力传播可以分解为该节点多个特征的影响力传播。在此基础上，郭等人。 [59]定义了多特征传播模型，并设计了多层网络结构的多重采样方法。然后，基于多重采样和鞅分析提出了一种改进的Revised-IMM算法[90]。

郭等人。 [91]提出了两种有效的解决方案：贪婪和通用TIM，以保护网络中的特定节点免受负面影响。其中，贪心算法采用爬山策略，得到了理论界，但时间复杂度较高。 General-TIM算法基于反向最短路径（Random-RS-Path）的随机采样，大大降低了时间复杂度。具体来说，如果边越多，则可以保护更多的节点覆盖随机 RS 路径被删除。因此问题转化为最大覆盖问题，即选择最少的边来覆盖尽可能多的随机RS路径。该算法首先需要采样Random-RS-Paths的数量，然后通过贪心法求解最大覆盖问题。为了降低算法的复杂度，基于真实网络的社团结构，提出了一种贪心算法。如果负面影响节点集合和目标节点集合没有出现在同一个社区中，则不需要考虑这些不相关社区中的边。去除不相关的社区后，贪心算法和General-TIM算法都可以得到显着的改进。实验结果表明，General-TIM算法虽然不能保证精确的逼近率，但在实际应用中可以获得良好的效果。

4.2.2. Methods for location aware IBM

在解决 IBM 问题时，一些算法利用节点的位置信息来估计影响的传播。朱等人。 [92]开展了位置感知影响块最大化（LIBM）研究，提出了两种基于四叉树索引和最大影响树状结构的启发式算法LIBM-H和LIBM-C[18]。给定一组负面影响节点，LIBM问题是选择正面影响节点来抑制负面影响在指定区域的传播。 LIBM-H中采用四叉树索引来存储节点的位置信息，并采用深度优先遍历从四叉树的根节点开始搜索位于查询区域的节点，最终得到最大影响力树结构(MIA)用于计算影响传播过程。 LIBM-H算法需要计算网络中所有具有阻塞负面影响的候选节点。但事实上，很多不重要的节点不应该被选为候选种子，因此不需要计算它们的阻塞负面影响。也就是说，为了提高种子选择的效率，我们只需要关注影响力大的节点，删除影响力小的节点即可。因此，他们提出了单元索引和节点索引来有效存储节点阻塞的负面影响，并提出了一种基于四叉树单元的更高效的算法LIBM-C。该算法首先将整个空间划分为小单元，并预先计算每个单元中节点的负面影响。然后，对于给定的查询区域，它聚合所有相应的单元格并使用上限方法来估计 top-k 正种子。

朱等人。 [93]还研究了竞争性社交网络（LTIBM）下的位置感知影响阻塞最大化问题，并提出了一种启发式算法LTIBM-H。该算法的目标是在给定的社交网络中找到一组正种子，以尽可能阻止负种子对位于给定区域中对某些主题有偏好的目标节点的影响传播。在LTIBM-H算法中，作者设计了一个QT树来获取给定查询区域的目标节点。接下来，利用 MIA 来近似种子的正面和负面影响传播。给定正负影响种子节点 SP 和 SN ，采用动态规划算法计算节点 v 的负激活概率 nap(v, SP , SN )。将节点 u 添加到正种子集中后，负激活概率的变化节点v的激活概率Bni(u, v)可以根据nap计算：

这里，β(v, T ) = Σzi=1 tiθi 是节点 v 对主题集的倾向。二元变量ti = 1表示阻止节点v对主题ti的负面影响的传播；相反，ti = 0 表示不需要阻止节点 v 对主题 ti 的负面影响的传播。在该算法中，只有影响力能够传入N(T,R)的节点才可以作为候选节点，N(T,R)是对主题T有偏好且位于R中的节点集合。让这些候选节点 Ca(T , R) 定义为：

最后，从 Ca(T , R) 中迭代选择 Bni(u, T , R) 最大的 k 个节点作为正种子集。实验结果表明，该算法能够达到与贪心算法相媲美的阻塞效果。 LTIBM-H 的结果优于其他基线算法。此外，LTIBM-H算法比贪心算法快四个数量级。 Zhu等人为了识别指定区域RQ中的k个节点来阻止RB区域中的负面影响传播。 [94]提出了IS-LSS算法，使用同花竞争独立级联模型来模拟影响传播。该算法对查询区域中的所有节点一视同仁，将所有节点视为正种子候选，主要分为两个步骤：第一步，使用四叉树索引结构来存储节点的位置信息，并使用深度优先遍历方法识别位于给定查询区域中的候选节点。第二步，最大堆用于存储候选节点及其被阻止的负面影响。然后使用MIA方法计算每个候选集的影响力，并使用动态规划算法计算它们的阻塞负面影响。最后，迭代选择最大堆中具有最大值的候选节点作为正种子节点。在此基础上，作者提出了改进算法IS-LSS+，它也使用最大堆来存储候选节点及其阻塞负面影响，但它使用上限方法和四叉树单元列表来删除不重要的候选节点。实验结果表明，随着正种子数量的增加，两种算法都实现了与贪婪算法类似的阻塞效果，同时运行速度比贪婪算法快四个数量级。

4.2.3. Hybrid technology-based methods

刘等人。 [95]设计了一种基于模拟退火的高效算法SA-min。他们将适应函数 c(G(D)) 定义为正种子集 D 对图 G 的影响。问题的目标是尽可能减少 c(G(D)) 的值。设系统初始温度T=T0，初始解为A，其邻域解为A*。如果满足 Δc = c(G(A*)) − c(G(A)) < 0，则表示解 A* 优于解 A，应将 A 替换为解 A*。如果 Δc ≥ 0，且 exp(−Δc/Tt ) 大于随机生成的阈值 ε，则 A 也应替换为解 A*。当迭代次数达到 q 时，当前温度 Tt 应减少 Tt = Tt − ΔT 。 Tt 是当前温度，当温度达到下限 Tf 时算法终止。如果使用蒙特卡洛模拟来计算影响力传播，SA-min算法的计算成本仍然较大，因此作者提出了一种高效的启发式算法ML_CS来模拟影响力传播，该算法仅计算节点的影响力距节点 v.

Jia 等人最多 m 跳。 [96]将IBM问题视为Stackelberg博弈问题，以负面影响节点为攻击者，抑制节点为防御者，寻求抑制节点的最优策略。作者首先提出了一种基于整数规划和约束生成相结合的方法。接下来，为了提高该方法的可扩展性，他们开发了一种近似解决方案，将问题视为整数规划，然后将松弛与对偶相结合以产生防御者目标的上限，以便可以使用混合整数线性规划进行计算。最后，他们提出了一种更具可扩展性的启发式方法，可以根据节点的度数从考虑集中修剪节点。

蔡等人。 [97]将IBM问题的研究与双预言机方法[98,99]结合起来，创建了一种新颖的启发式预言机。该策略中双预言机算法的优点之一是可以轻松更改预言机以生成现有算法的新变体。该算法还具有很强的能力来模拟各种攻击者/防御者的最佳响应策略，并更彻底地测试启发式算法的性能。

杨等人。 [8]提出了基于扩散动力学的启发式算法贡献者识别（ContrId）和ProxContrId来解决IBM问题。基于负面影响传播的动态，他们通过识别对负面影响传播贡献最大的节点（称为贡献者）并阻断从负面影响种子到其余网络节点的重要路径来抑制负面影响传播。他们根据正种子的搜索空间将启发法分为两类：无约束和约束。在无约束方法中，可以在集合V\SR中任意选择一个节点作为正种子节点，其中SR是负种子集。假设tv时刻激活的节点v的贡献是通过在任意t>tv时该节点激活的节点Nout v的数量来衡量的。假设影响传播在时间Ts达到稳定状态，则每个时间段受负面影响激活的节点集合定义为φRt(t=1，...，Ts)。令 L 为网络中最长简单路径的长度，并满足 Ts ≤ L。因此，对于每个节点 v ∈ φR t ，其贡献 Ctr(v) 定义如下：

将不活跃节点的贡献度设置为0。最后，ContrId算法选择贡献度最高的k个节点Ctr(v)作为候选种子节点。 ProxContrId算法将负种子的影响传播空间限制在区域Nout (SR) = ((⋃ v∈SR N out v ) \ SR)。由于搜索空间较小，受约束方法的时间复杂度比无约束方法低。张等人。 [31]提出了一种主导影响算法，由两个子算法组成：DI-网关节点检测和DI-候选选择。 DI-网关节点检测识别网关节点，对于扩大错误信息的影响力具有重要意义。在错误信息的扩散自然终止之前，DI-候选选择找到不同搜索轮次的候选种子集，这些种子集由网关节点集确定。最后，支配影响算法获得积极信息的最佳种子。实验结果表明，Domining Influence算法比MinGreedy、Random等启发式算法取得了更好的性能，更适合大规模网络。

4.3. Methods simulating immunology process

IBM问题通常采用常见的免疫控制策略。基于免疫学的IBM方法可以分为两类：基于全局信息的免疫策略和基于局部信息的免疫策略。基于全局信息的免疫策略需要了解网络结构的完整信息。中心性越高的节点往往具有更大的传播影响力。基于免疫学的算法首先根据节点的中心性对节点进行排序。然后，可以选择合适的免疫靶点来阻止疾病的传播[14,100–108]。

黄等人。 [109]提出了一种顶点着色的免疫策略，将着色节点分为不同的集合，然后从包含最多节点的集合中选择免疫节点。然而，在连接免疫节点的边之后，网络被划分为多个子图，并且免疫策略将许多资源分配到小尺寸的子图中。针对这种情况，陈等人。 [110]提出了一种等图划分的免疫策略，通过将原始图划分为大小几乎相同的连通子图，大大减少了需要免疫的节点数量。例如，对于流行病传播的动态过程，Zhang等人。 [111]提出了三种有效的多项式时间启发式算法DAVA、DAVA-prune和DAVA-fast，可以帮助公共卫生专家根据当前的疫情分布做出实时场景。主特征向量（PEV）在不同网络子图上的位置是重要的信息，可用于修改和控制由网络拓扑介导的动态过程。帕斯托-萨托拉斯等人。 [112]提出，根据PEV的位置，高免疫个体的效果可能完全不同

虽然基于全局信息的免疫策略可以更准确地识别关键节点，但随着网络数据多源异构的趋势，对于大规模网络我们很难及时获取网络的全部信息，而且网络结构的计算复杂度也较高。而基于局部信息的免疫策略由于只利用节点周围的局部信息，因此更加实用和可操作。该策略可以快速高效地识别免疫目标，阻断疾病在全网的传播。随机免疫策略是一种局部信息免疫策略，通过随机选择网络中的部分节点来进行免疫。无论是单层网络还是多层网络，都需要免疫大量个体来阻止负面影响的传播，并且可能需要免疫80%以上的节点来阻止负面影响的传播[113,114] 。比如在病毒传播方面，对于像新冠病毒这样传播能力强的流行病，很多国家都实施了成本高昂的全民免疫策略。为了解决这种情况，科恩等人。 [115]提出熟人免疫策略，首先随机选择一个节点进行免疫，在下一次节点选择过程中，仅随机选择免疫节点的邻居，直到达到设定的免疫比例。为了避免对同一组邻居进行过度免疫，Holme 等人。 [116]通过用最大连接边数来免疫邻居，对熟人免疫策略进行了相关改进。夏等人。 [117]使用节点的度和聚类系数作为免疫节点选择的标准。郭等人。 [118]提出了一种欧几里德距离首选（EDP）模型，它产生了一个小世界网络。在此基础上，他们提出了免疫半径的概念，将免疫节点的选择限制在有感染节点的半径r范围内。实验表明，免疫半径能够有效抑制疫情，并且对EDP模型参数变化具有鲁棒性。

然而，通过节点免疫策略，免疫实体与网络的其余部分完全隔离，网络的连接性被破坏[119]。因此，仍有部分研究通过对网络的重要边缘进行免疫来实现疫情传播阻断[120-129]。为了阻止疫情在复杂的社交网络上传播，张等人。 [130]提出了一种根据边缘重要性删除边缘的方法。边的重要性是连接该边的两个节点度的乘积。与其他方法如随机免疫、比例免疫、定向免疫、熟人免疫等主要关注如何去除节点以实现对复杂网络上疫情传播的控制相比，该方法更能有效地实现对复杂网络上疫情传播的控制。复杂网络，并且能够更好地维护复杂网络的完整性。张等人。 [131]将边的重要性定义为它所连接的两个节点的强度的乘积。节点的强度可以是连接该节点的所有边的权重之和，也可以是通过该节点的最短路径数量的总和或乘积[132]。库尔曼等人。 [133]提出了离散动力系统模型下的边缘覆盖启发式算法。该算法识别并去除网络组的边缘，以阻止负面影响的传播。进行实验来模拟阻塞前后受感染节点数量的影响。实验结果表明，与基于阈值的启发式算法[83]和高度启发式算法[130]相比，边缘覆盖方法在阻止未加权图和加权图的负面影响传播方面更有效。此外，作者发现，在平均度和平均聚类系数较低的网络中阻止传播更加困难。

为了抑制流量驱动的负面影响的爆发，杨等人。 [134]发现，可以通过阻止大度节点之间的连接边或阻止具有较大边缘网格的连接边来减少负面影响的传播。与去除介数最大的边相比，阻塞连接大度节点的链路对于提高流行度阈值更有效。受免疫学的启发，陈等人。 [135]提出了一种近似最优可扩展算法NetShield和相应的改进算法NetShield+来寻找一组具有最高屏蔽值得分的节点。该算法首先利用网络邻接矩阵的最大特征值λ来衡量网络的脆弱性。然后，利用矩阵微扰理论的结果定义每组节点的屏蔽值得分Sv。最后，使用子模块理论来找到一组具有最高屏蔽值得分的节点。网络的脆弱性与网络中边的数量和位置信息密切相关。采用邻接矩阵A的最大特征值λ作为网络的脆弱性测度，即λ值越大，表明网络的脆弱性越高。

4.4. Methods exploiting community structures

基于社团结构的IBM方法认为网络中的节点之间具有一定的聚类特征，相似度较高的节点被分到同一社团中（如图5所示），该方法一般可以反应关系更有效地构建社交网络模型。为了提高 IBM 算法的效率，基于社交网络中影响扩散的局部性，Lv 等人。 [139]提出了一种基于社区结构的IBM算法CB_IBM。根据社区Ci中影响力种子节点的分布情况，首先确定种子节点ki的数量。然后选择影响力最大的 ki 节点作为正向影响力的种子节点。两个实验结果真实网络表明，CB_IBM 的阻塞效果与 Greedy 的性能一致，并且 CB_IBM 比 Greedy 快得多。

阿拉兹哈尼等人。 [140]提出了一种名为 FC_IBM 的基于社区的算法，使用模糊聚类和中心性度量来寻找候选节点的良好子集，以传播解决 IBM 问题的积极信息。该算法首先使用基于局部随机游走的新度量来比较每个节点之间的相似性。其次，为了尽可能保持原始节点距离，通过多维缩放将网络结构映射到低维空间。接下来，使用模糊 c 均值将节点聚类成社区。最后根据中心度高的原则选择有影响力的节点。与没有进行社区检测的算法相比，该算法可以有效降低节点被负面影响节点感染的概率。与传统的影响力抑制问题不同，Nguyen 等人。 [141]解决了信息可以以任意概率传播的问题。他们不仅考虑了防御者是否知道被错误信息污染的初始节点集，而且还考虑了防御者遏制错误信息传播的时间余量。阮等人。改进了爬山算法[142]，提出了贪婪病毒停止器（GVS）算法，将每轮边际增益最大的节点作为候选种子节点，直到满足终止条件。但该方法时间复杂度较高，不适合大规模网络。因此，他们提出了一种基于社区结构的启发式算法。该算法首先通过Blondel算法[143]将网络划分为社区，并根据社区所包含的节点数量将社区按降序排列，然后对每个社区应用GVS算法，找到一组有影响力的节点来抑制负面影响。最后，在每个社区中贪婪地选择提供最大边际收益的节点，作为候选种子节点。实验结果表明，该算法虽然可以取得较高的效果，但如果应用在没有社团结构的网络上，效果未知。

通过观察网络中社区的结构特性，Fan 等人。 [58]发现存在一组称为桥端的节点。每个桥端在与其相邻的负面影响节点所在社区中至少有一个直接相连的邻居，并且该社区内的负面影响节点可达。 OPOAO模型下，通过保护部分桥端来抑制负面影响。对于每个负面影响节点，通过广度优先搜索（BFS）方法构建谣言前向搜索树（RFST）来找到所有桥端，然后将它们放入候选集中。他们证明了问题的目标函数具有子模性，最后利用贪心算法选择对桥端保护贡献最大的节点作为抑制种子节点。此外，在DOAA模型下，他们将IBM问题等同于集合覆盖（SC）问题，并提出了基于集合覆盖的贪婪（SCBG）算法。其主要思想是：给定谣言发起者集合SR和桥端集合B，对于任意v∈B，使用BFS方法构造v的以v为根的桥端向后搜索树（BBST）Qv。用 Q1、Q2、... 表示。。。 , Q|B|所有桥端对应的 BBST。然后对于每个 u ∈ Qi, 1 ≤ i ≤ |B|，检查所有其他 BBST，即 Qj (j ̸= i, and1 ≤ j ≤ |B|) 找到包含 u 的并记录它们，然后连接它们的根到节点u。这样一棵1跳树就形成了，u被标记为新创建的1跳树的根。让 SWu 表示这棵树中的所有叶子。然后他们应用贪心算法从SWu覆盖B中所有节点的集合中选择最少数量的集合。最后，这些节点构成了保护者发起者的集合。郑等人。 [144]认为，在负面影响节点的邻域社区中，桥端会比社区其他部分更早传播到负面影响节点。如果桥端节点受到保护，那么负面影响节点将不会传播到社区的其他节点。然后，IBM 问题被概括为通过从网络中删除子集中的节点及其输入和输出边来识别最小节点的问题。为了解决这个问题，他们提出了基于贪婪的最小顶点覆盖算法（MVCBG）。为了保护所有桥端免受负面影响，直观的方法是使用深度优先搜索方法获得负面影响节点与桥端集合之间的所有简单路径，然后尝试以最小的长度阻塞所有这些简单路径节点数。然而，由于这些简单路径的数量非常多，因此很难在短时间内全部识别出来。因此，为了简单起见，它们仅屏蔽所有起点为负面影响发起者或可能受到负面影响的节点、终点为桥端的边，屏蔽最少数量的节点，从而防止谣言不影响任何桥端。该算法在某些数据集中效果良好，但运行时间较长，不适合大规模网络。

4.5. Methods for specific constraints

4.5.1. Resource cost constraint

在现实应用中，为了阻止负面影响的传播，选择每个正面种子节点通常需要一定的成本。例如，企业通过明星代言扩大影响力，击败竞争对手，占领市场份额。但每个明星的出场费都不同，公司的广告费用也有限。如何以有限的成本发挥最大的影响力是一个值得研究的问题。利头等人。 [35]利用模拟退火方法在有限的成本下确定最合适的种子。该方法基于贪心策略，迭代地选择种子节点加入集合S。当达到所需的种子数k，或者满足终止条件时，迭代终止。模拟退火在寻找最优解的过程中引入了随机因素。它以一定的概率接受比当前解更差的解，因此可以避免局部最优解而达到全局最优解。实验结果表明，该方法能够逼近最优解。当应用于实时应用时，选择1000个种子节点的时间不超过23分钟。陈等人。 [148]研究了具有成本约束的复杂网络的影响传播模型。他们使用叠加随机游走策略来衡量网络的影响传播。为了降低算法的时间复杂度，将影响传播控制在某个子图的范围内，并提出了抑制负面影响传播的有效方法。在此基础上，引入渗流的思想来确定约束节点集合的大小。实验结果表明，该算法不仅能够有效限制负面效应的传播，而且在成本约束下取得了较好的性能。施等人。 [149]通过有限成本下的自适应资源配置策略来抑制负面影响。他们的结论是，负面影响传播过程中的不同时间段可能会出现不可预见的特殊情况，因而不同时间段所需的镇压资源成本也不同。例如，在t时刻，负面影响传播缓慢，因此只需要少量的成本来抑制负面影响，即剩余的资源可以用于后期的分配。图6示出了自适应资源分配的示意图，其中网络拓扑如图6(a)所示，感染节点用红色表示，抑制节点用绿色表示，黄色节点受到抑制节点的保护，红色箭头为负面影响传播路径。假设S在第一轮传播中以1/2的概率感染节点A、B、C和D，在第二轮传播中，被感染的节点将以100%的概率感染其邻居。从图 6（b）可以看出，如果 S 在第一轮感染节点 A 和 B，并选择节点 A 和 B 作为抑制节点，则节点 A 和 B 可以保护 14 个节点免受感染。然而，如果S在第一轮中感染了节点C和E（如图6（c）），则可以看出节点A和B在第一轮中未能保护其余节点。此时，我们可以释放资源A和B，并将D和F设置为第二轮传播的抑制节点，即可完成对剩余节点的有效保护。

4.5.2. Uncertain influence source

现有算法的设计通常假设在 IBM 问题的种子节点选择过程中负种子集的来源始终是已知的。然而，在真实的社交网络环境中，由于社交网络的隐私规则，很多时候我们只知道负种子的分布情况以及每个节点成为负种子的概率，很难知道负种子的确切来源。负面影响。负面影响源的分布用来描述负面种子的不确定性，可以通过经验知识或用户行为观察来估计。在这种情况下，如何最大限度地阻断来自不确定来源的负面影响传播，引起了学者们的关注。陈等人。 [150]将该问题定义为不确定源的负影响块最大化问题（IBM-US），并提出了一种基于采样的IBM-US-SB-Seed算法来实现IBM-US问题的近似解。设H为分布概率p−下所有可能的负种子集的集合，C和D分别为正种子节点和负种子节点。定义g(c)为正、负种子联合影响下的负影响阻止期望值，计算公式为：

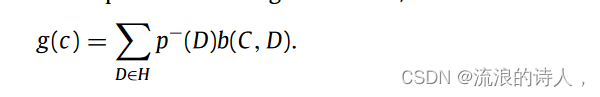
这里，负面影响阻止 b(C , D) 是正面种子集 C 减少负面激活节点。因此，IBM-US问题是找到一个满足以下条件的最优正种子集C*：

因为H的大小与种子节点的数量有关，即：H = 2|V|，如果节点总数很大，那么H呈指数增长。由于直接优化方程是不切实际的。 (31)式中，根据节点v的概率分布p−(v)，采用采样的方法来选择负种子节点集合。设N为采样到的负种子节点集合的个数，用HN = { D1、D2、. 。。 , DN } 分别。令C*N为基于HN中的负种子集获得的最优种子集。 C ＊ N 用于近似C ＊。 HN 中集合 Di 的概率 p−(Di) 选择为：

4.5.3. On signed networks

目前大多数关于 IBM 问题的研究都集中在未签名的社交网络上，而忽略了节点之间关系的极性。在签名的社交网络中，每个链接可能代表其连接的用户之间的积极关系（例如，朋友或喜欢）或消极关系（例如，敌人或不喜欢）。忽视用户之间关系的这种极性可能会导致高估积极影响，并在实际应用中造成不利影响。因此，一些学者也针对签名网络上的IBM问题进行了相关研究。一些研究使用贪婪算法来解决签名社交网络中正面影响或负面影响最大化的问题[29,153–155]。尽管贪心算法可以实现良好的近似，但它们的计算成本很高并且效率不够。李等人。 [156]提出了一种基于模拟退火的种子节点集选择方法，以解决签名社交网络中扩展独立级联模型下的积极影响最大化问题。除此之外，他们还开发了两种启发式，即距离限制和单节点积极影响启发式，以加快其方法的收敛过程。近年来，人们提出了许多新的相反影响扩散模型和在符号网络中最大化积极影响扩散的方法[157,158]。积极影响最大化算法的效率和准确性得到了极大的提高。然而，在上述现有工作中，有两个因素阻止他们在签名网络中的积极影响最大化问题上获得高质量的结果，第一个是因为很少有人考虑负边在影响传播中的重要性。第二点是，许多方法在选择候选种子集时通过蒙特卡罗模拟来估计影响传播。因此，为了解决这个问题，盛等人。 [159]观察到负边沿比正边沿发挥更重要的作用。他们提出了基于传播规则的反向影响传播模型，并定义了影响传播函数，以避免模拟正向影响并减少计算时间。最后，提出了一种种子节点选择算法PIM-SC，以获得符号网络中最大的正向影响传播。该算法通过影响力传播函数计算种子节点的传播增量，然后采用贪心策略依次选择种子节点。具体流程如下。令 d+ t (S, u, +) 和 d+ t (S, u, −) 为节点 u 的正边和负边在时间 t 收集的正向影响。类似地，令 d− t (S, u, +) 和 d− t (S, u, −) 为节点 u 的正边和负边在时间 t 收集到的负面影响。根据本文定义的相反影响传播规则，如果边（v，u）是正边，则节点u将在时间t以概率P（v，u）被激活为正（或负）状态。类似地，如果边 (v, u) 是负边，则节点 u 将以概率 P(v, u) 在时间 t 被激活为负（或正）状态。则可以得到节点u在不同情况下受到的影响：

4.5.4. On dynamic network

斯卡曼等人。 [160]研究了使用实时信息在网络中分配治疗资源以抑制病毒的扩散。首先，他们提出了一个动态资源分配问题（DRA）的模型公式。然后，他们提出了感染边缘最大减少（LRIE）控制策略，该策略最小化抑制病毒扩散成本的二阶近似。他们分析说，这种方法最大限度地减少了可以将感染传播到健康节点的感染边缘的数量，从而减少了感染在网络中的分散。对各种随机生成的网络和现实世界网络的模拟表明，所提出的 LRIE 策略是比较策略中最有效和最鲁棒的。此外，尽管IBM问题已被广泛研究，但现有的大多数工作都忽略了截止日期和影响传播延迟的影响。在许多现实情况下，例如总统选举，必须遵守最后期限，以尽量减少错误信息的传播。受到安全带解决方案的启发，Manouchehri 等人。 [28]研究了时间IBM并提出了一种基于采样的算法TIBM-M。该算法首先计算所需样本的数量，然后通过生成样本将IBM问题转化为最大覆盖问题。最后利用贪心法寻找抑制影响节点。实验表明，TIBM-M算法在效果上与贪心算法一致，能够显着提高效率。在社交网络中，当受感染节点的百分比随着时间的推移达到一定阈值时，就会引起相关当局的注意，进而发现网络中负面影响的传播者。一旦发现有负面影响的节点，相关部门就会对其进行封杀。图7显示了基于从新浪微博提取的数据的几个典型的主题演化曲线。 Wang 等人基于 Ising 模型 [62]。 [61]提出了一种结合全球负面影响流行率和个人倾向的动态负面影响扩散模型。他们还引入了用户体验效用的概念，并提出了效用函数的修改版本来衡量效用与阻塞时间之间的关系。然后，他们利用生存理论来分析在用户体验效用的约束下节点被激活的可能性。最后提出了基于节点选择策略和最大似然策略的贪心算法和动态分块算法。该算法提出谣言全局话题流行度的概念来描述一种常见的社会现象，即当负面影响传播一段时间后，可能会产生一种“负面影响氛围”，影响网络社交的判断或决策。网络用户。假设在时间 t0 检测到负面影响，贪心算法的目标是最小化激活的节点数量在时间 t1 受到负面影响。在t1时刻，根据生存理论，节点被激活的概率定义如下：

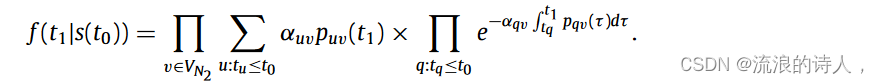
5. Applications of influence blocking maximization

IBM 的问题是识别一小部分节点，以在给定的扩散模型下最大化阻止负面影响传播。它在谣言抑制、疫情控制、竞争性营销、识别意见领袖、预防交通拥堵等许多应用中都有明确的实际动机。下面我们将回顾近年来的一些进展。

5.1. Rumor suppression

由于在线社交网络促进了信息的快速、广泛传播，网络上也出现了不同形式的谣言[21,161]。与真实消息相比，谣言的传播速度更快、范围更广，更容易影响用户的判断。因此，这种在网上呈现的虚假信息可以迅速改变舆论并引起社会恐慌[9,22]。 IBM 的一个重要应用是社交网络中的谣言控制。因此，一些学者对社交网络中抑制谣言等负面影响的方法进行了广泛的研究，包括谣言传播模型和抑制算法。其中，谣言传播模型的过程与网络中病毒传播的过程类似。因此，谣言传播主要基于经典流行病模型或其改进版本[10,11,50,54,162,163]。谣言抑制算法主要包括屏蔽谣言节点[14,58,61,63,64,69,72,73]、屏蔽谣言链接[8,23,24,75–77,80,83,160,164]和抑制谣言的方法通过积极影响[5,6,38,87,165–169]。张等人。 [170]认为用户是谣言的被动接受者，谣言应该通过用户的浏览行为传播，并基于随机游走模型对谣言的传播进行建模。基于此，提出了一种基于 RanSel 的排序方法，选择 k 个节点作为“保护者”，以保护尽可能多的节点免受谣言的影响。李等人。 [165]认为，在谣言传播过程中，被谣言污染的节点并不一定成为谣言传播者，因为后来出现在互联网上的正确信息使他们做出正确的判断。比如，如果有学生在班里散布“因为疫情，期末考试取消了”的虚假信息，整个班级就会被谣言污染，但每个学生也会有自己的判断关于该消息。当网络中受保护的节点发布“下周期末考试”的正确信息时，受污染的节点就会做出自己的决定，并可能传播真实的信息。基于这个想法，他们提出了γ−k谣言抑制问题，通过在污染集中找到γ×k个保护器和在未污染集中找到(1−γ)×k个保护器来保护网络，如图8所示。，分别为线性阈值模型和独立级联模型设计了近似比率为 1 − 1/e 的贪婪近似算法。该算法在三个真实的社交网络上进行了测试：NetHEPT (http://arXiv.org)、WikiVote (http://snap.stanford.edu/data/wiki-Vote.html.）和Slashdot0811（http://snap.stanford.edu/data/soc-Slashdot0811.html.），实验结果表明可以实现更好的性能。他等人。 [168]提出了一种实时优化策略，能够在预期时间段内以最小成本抑制谣言的传播。为了避免谣言传播对社会造成巨大威胁，他们还提出了脉冲策略，能够定期在网络中传播积极影响。这两种策略在digg2009数据集上都取得了优异的性能（http://www.isi.edu/lerman/downloads/digg2009.html）。

童等人。 [27]研究了存在多个正级联时的谣言阻止问题。通过制定谣言感知博弈和谣言遗忘博弈，他们表明在最佳响应和近似响应下，均衡策略和博弈策略都提供了 2 近似和 (2e + 1/e + 1) 近似社会效用，即不受谣言影响的节点数量。霍斯尼等人。 [166]提出了传播过程的HISB模型，该模型描述了多路在线社交网络中谣言的传播（如图9所示）。基于该模型，他们从网络推理的角度并运用生存理论，提出了一种真相运动策略，以最大限度地减少多重在线社交网络中谣言的影响。该策略通过在检测到谣言后立即选择最有影响力的节点并开展真相活动来提高对谣言的认识来防止谣言的影响。霍斯尼等人。 [167]发现社交网络中的每个用户对于谣言都有不同的态度和想法。他们可以根据自己的经验和知识来支持、质疑和反对谣言，这种态度对谣言的传播起着重要作用。例如，推特上对于“奥巴马是穆斯林”的谣言有不同的看法，每个用户都有不同的态度和想法，如图10所示。

基于这种考虑，Hosni 等人。 [167]提出了一种基于马尔可夫链模型的新方法，将个体对谣言的不同态度整合到HISB模型中。这个过程考虑两个极点：支撑并拒绝极点。然后，他们假设从一极到另一极的转变至少应该通过对谣言的中立或质疑意见。提出一种动态阻塞期（DBP）方法来求解多谣言影响最小化问题。每个选定节点的阻塞时间是根据其在社交网络中的活动来估计的。该解决方案是利用生存理论从网络推理问题的角度制定的。因此，提出了一种基于似然原理的算法来选择最有可能被感染的节点并支持谣言。这种方法屏蔽了对大量谣言传播贡献最大的节点。这些节点将被封锁一段时间，以避免对用户在 OSN 中的体验造成负面影响。该算法可以保证最优解的逼近率在63%以内。图11是DBP算法的性能图。

图 11 给出了当谣言数量 RN 分别为 2、4、6 和 8 时，最终受到谣言影响的个体数量比例。从图11中可以看出，被选为阻塞节点的比例K值越大，受谣言影响的比例越小。图12显示了不同算法可以减少谣言传播中感染人数的百分比。

可以看出，算法DBPA在不同场景下都比其他算法有更好的性能，并且可以最大限度地减少谣言对传播的影响。

5.2. Epidemic controlling

IBM问题的另一个重要应用是预防流行病传播[15,70,171–178]。新冠肺炎疫情在不到两个月的时间里席卷全球，病毒在人群中肆意传播，并呈现不断扩大的趋势。这次疫情的蔓延导致了世界经济的巨大危机，歧视疫情严重国家的人民将是对人类的巨大挑战。在各种疫情防控措施中，疫苗接种是最有效的策略之一。更高的疫苗接种覆盖率可以提高疾病传播和控制的临界阈值，或中断病毒在复杂网络上的传播[135,179–182]。

薛等人。 [183]研究了在缺乏全局网络结构信息的情况下控制网络上疫情传播的分布式链路运行问题。他们将原始问题近似为涉及相邻矩阵特征向量的问题。通过事件触发通信的设计，分布式PI估计算法最终赋予局部个体特征向量的全局知识。图13显示了三个随机数据集中不同策略的流行阈值随边缘删除的变化趋势。马塔马拉斯等人。 [124]提出了一组离散时间控制方程来评估边缘对复杂网络中传播过程的贡献。结果用于制定流行病遏制策略，该策略基于递归地停用具有最大链接流行病重要性的链接，同时保持整个网络的连接性，即避免碎片化。图14是航空运输网络中不同策略的疫情防控示意图。结果开辟了一种在边缘而不是节点级别分析复杂网络动态扩散模型的新方法。巴萨拉斯等人。 [120]考虑了流行病传播的动态因素，提出了一种名为关键边缘检测器（CED）的算法，该算法根据关键连接的扩散能力来检测关键连接。通过每一步中有限数量的动作删除，这些边将构成免疫目标，以保存复杂网络的最大可能部分。图 15 显示了不同方法的性能与两个数据集（http://konect.unikoblenz.de/ 和 http://snap.stanford.edu/data/index.html）中影响概率 λ 的函数关系。。李等人。 [121]提出了一种独立于初始感染源的Limited-Temporary-Links-Removed策略。无论初始感染源是单个还是多个、同时还是分散，该策略通过暂时移除或调节网络中病毒传播最短路径上的重要边缘，使病毒绕过或被阻断。可以有效减缓病毒传播、控制病毒传播范围，同时保证网络系统的基本功能不受影响。古斯里亚迪等人。 [128]提出了一种分布式算法来估计特征向量并验证网络的连通性。通过模仿在每次迭代中从网络中删除一个或多个链接的基于梯度的方法，可以有效地计算次优解决方案，以解决维持网络连接性同时减慢或停止网络中疾病传播的问题。图 16 显示了随着随机数据集中删除的链接数量增加，不同策略的传播阈值的趋势。目前，疫情传播网络大多呈现社区结构，社区中心和桥梁是影响力节点，在疫情传播中发挥关键作用[184-190]。在疫情传播网络中，存在重叠的社区和重叠的节点，它们在疫情传播中发挥着重要作用。因此，可以考虑每个社区中重叠节点的数量来进行免疫节点选择[191]。严等人。 [192]认为全局或局部策略的选择取决于网络社区之间的紧密程度。如果社区联系紧密，则全局政策效果更好，否则本地政策效果更好。

5.3. Competitive marketing

在线社交网络的日益普及促进了信息、观点和新产品的广泛传播，为“病毒式营销”提供了巨大的机会。在现实的市场场景中，往往会有多家企业销售同类型的产品，不同的企业都希望通过开展有竞争力的营销策略来获得口碑效应的利益最大化，从而击败竞争对手，占领市场份额。 193-198]。例如，当苹果、华为和三星等公司生产最新的手机时。每家公司都试图说服客户购买其产品，并在新兴市场中占据比竞争对手更大的地位。因此，IBM技术可以用来在竞争市场中最大化利益[85,86,89,93,97,145,199,200]。在病毒式营销中存在两种或两种以上竞争产品的情况下，企业可以利用用户之间的信息交互来传播其产品的认知度。吴等人。 [201]通过选择网络中对产品营销有影响力的种子集，最大化社交网络中竞争影响力的传播。首先，根据网络中边的传播概率建立可能性图[202,203]，然后设计竞争影响力传播模型（CISM）来模拟可能性图下的竞争传播。基于这个可能性图，作者使用成本有效的惰性前向（CELF）算法[204]来选择竞争种子节点。吴等人。 [88]提出了一种启发式算法CMIA-H来寻找一组传播对自己有利的信息的用户。他们还提出了一种启发式算法CMIA-O，通过最大限度地封锁竞争对手的信息范围来抵消竞争对手信息的传播。该算法在四个真实数据集上进行了测试和验证：EMAIL（包含1.13K节点）、NetHEPT（包含15.2K节点）、NetPHY（包含37.2K节点）和DBLP（包含65.5K节点）。例如，图 17 中 EMAIL 数据集的实验结果表明，随着正种子（有利于自己的节点）数量的增加，不同的算法可以减少负种子（有利于对手的节点）激活的节点数量。因此，从图中可以看出，该策略可以有效阻断不良影响在网络中的传播。这也充分说明该方法在市场竞争的场景中具有时效性，能够快速为商家提供优秀的策略。

在市场经济中，经常存在一种现象，企业新开发的产品只在某个地区销售，而不是在全国范围内推广。因此，企业需要做的就是如何让产品能够在指定区域的竞争中击败竞争对手，从而占领该区域的市场份额。朱等人。 [92]将这种情况转化为如图18所示的位置感知影响阻塞最大化（LIBM）问题，并提出了两种基于四叉树索引和最大树结构的启发式算法LIBM-H和LIBM-C。他们在三个真实世界数据集 Ego-Facebook、Brightkite 和 Gowalla(http://snap.stanford.edu/data) 中进行了实验。 Ego-Facebook 是一个源自 Facebook 应用程序的小型社交地图。数据集中，每个节点对应一个用户，而边则对应彼此之间的好友关系。 Brightkite和Gowalla都是一种数据集，用户通过签到来共享他们的位置，其中节点是用户，两个节点之间的边意味着他们具有朋友关系。由于贪心算法在大型网络中运行速度非常慢，因此作者在 ego Facebook 数据集（包含 4039 个节点）上选取度数最高的 50 个节点作为负种子，来模拟不同算法在小、中、大网络中阻止负效应的效果地区。实验结果如图19所示。从图19(a)到(f)可以看出，LIBM-H和LIBM-C算法在所有条件下都比其他启发式算法具有更好的效果。另外，从图19（g）到（h）可以看出，在任何模型下，LIBM-H和LIBM-C算法的运行时间只需要几秒，超过四个数量级比贪心算法更快。类似地，在大型社交网络Brightkite（包含58K节点）和Gowalla（包含197K节点）上的实验结果如图1和2所示。 20 和 21. 从从图中可以看出，LIBM-H和LIBM-C算法在设定的查询区域内具有优异的分块效果，这意味着企业可以通过该方法选择积极的影响力节点，在降低影响力的同时扩大自家产品的影响力从而占领特定领域的市场份额。

5.4. Online social media monitoring

在线社交媒体是人们相互分享意见、见解、经验和观点的工具和平台。在线用户能够通过他们在网上看到的新的、有趣的事物或关于自己的博客来传播信息。例如，Twitter目前拥有超过3.5亿活跃用户，每天有近1.9亿用户访问。 Twitter 上的用户不知疲倦地在 Twitter 上发布新的、有趣的想法、网站、新闻、音乐和视频链接，这些链接在各个层面上得到转发，并迅速传播到世界各地。当一个想法突然在社交媒体上流传时，无论这个想法是好是坏，都需要找到该想法传播中的一些重要节点或重要路径，因为这些信息可能会对正面信息的传播产生负面影响[12]。其中重要的一项研究策略是找到一些被称为意见领袖的人。这些意见领袖可以在网络信息传播过程中对大多数其他个体的意见、决策和行动产生影响。即使普通个人的最初意见与意见领袖的意见不同，意见领袖最终也能引导普通个人接受他们想要的意见[19,205-207]。例如，用户在网络中拥有的关注者越多，该用户就越有可能成为意见领袖，而如果用户只是保持运行记录，则根本没有人愿意关注他/她。因此，要想正确的观点获得更多的支持者，控制负面观点的传播，最重要的方法之一就是挖掘网络中的意见领袖，并获得他们的支持。

雷曼等人。 [208]通过使用各种基于中心性的指标和基于社区的检测方法，在推特上确定了关于“发现新粒子”主题的意见领袖。如图22所示，Twitter上的用户之间存在三种类型的交互，即回复、转发和提及，作者将Twitter数据集分为三个子网络：回复网络、转发网络和提及网络。此外，根据用户的入度和出度之间的关系，区分出五个关键用户：对话发起者用户、影响者用户、活跃参与者用户、网络构建者和信息桥梁用户。不同的用户及其交互模型如图 1 和 1 所示。 23和24。其中，对话发起者用户几乎都是入度节点，而影响者用户是具有更多入度和一些出度的节点，并且影响者充当网络中的意见领袖，因为其他用户在网络中转发并在推文中评论影响者。网络中的活跃参与用户是具有大量出度而很少或没有入度的用户。网络构建者用户是链接两个或多个影响者的节点。信息桥梁用户是连接影响者和活跃参与者的节点.

如图所示。如图25-27所示，这三个网络都有社区结构，有助于网络中信息的快速传播[209]。从图中可以看出，许多低度节点与对话发起者或影响者连接，这些节点不与其他节点共享信息，因为它们只想从意见领袖那里获取最新信息。例如，在图25（a）中，可以看出Reply Network被Yifan Hu算法[210]划分为10696个社区。图的边缘是离散的小社区，图中心的一些彩色社区是对话发起者和影响者所在的社区，社区内的信息由于这些意见领袖的存在而传播得非常快。

图25（b）显示了从网络中删除离散节点和社区后的过滤网络，虽然只剩下8个社区，但仍然包含超过15％的节点和21％的边。图25（c）显示了不同社区的颜色以及该社区中节点的百分比。因此，在识别出意见领袖后，可以将其作为正向种子节点，影响竞争网络中的其他节点，阻断负面影响的传播。此外，还可以利用信息桥梁节点切断负面影响者与个人之间的联系，阻断负面影响的传播。大多数关于竞争性信息传播及相关问题的研究都集中在传统社交媒体，例如 Twitter 和 Facebook [74]。近年来，出现了一些基于消息的社交网络（Msg-SN），例如微信，它们通过在朋友圈中发布图片、文本和网络链接来传播信息[211]。

联系人列表中的朋友。由于Msg-SN中大多数用户的好友数量较少，仅凭好友数量很难找到拥有数百万粉丝的关键意见领袖。为了找到这样的关键意见领袖来阻止负面影响信息的传播，姚等人。 [66]提出了一种基于特征向量中心性的启发式算法，在竞争线性阈值模型下选择用于阻止负面影响的正种子集。他们收集了超过 24,000 个用户和 42,000 条浏览和分享记录的真实微信数据，并将数据按照时间段分为 WM 数据集 1 和 WM 数据集 2。 WM数据集1涵盖了2016年1月8日至14日的数据，WM数据集2涵盖了2017年10月1日至7日的数据。在微信数据集1中，作者将度数最大的前50个节点作为负节点，并使用他们传播负面影响，然后通过选择正面种子来封锁负面信息。实验结果如图28所示。

从图28（a）中我们可以看出，当选择的正种子数量较少时，基于度中心性的策略可以取得更好的效果。这是因为微信的网络图比较稀疏，信息很难在网上大规模传播，而大度节点在阻断负面种子的扩散路径中发挥着重要作用。随着正种子节点数量的增加，虽然所有计数策略的阻塞效果越来越好，但大度节点并不总是出现在负种子的影响力扩散路径中。在这种情况下，特征向量中心性算法和CLDAG算法可以获得更好的分块效果。图28（b）显示了通过不同策略选择150个积极种子以防止网络中负面影响传播的运行时间。从结果可以看出，贪心算法需要10多个h才能完成阻塞，而特征向量中心性算法只需要50.84 s。接下来，他们在两个具有较大负种子集的 WM 数据集上进行了实验。在每个数据集上，分别通过最大度策略选择节点和随机选择节点策略生成300个节点的负种子集。测试不同策略的阻塞效果的结果如图29所示。在WM数据集1上，当选择大节点作为负种子集时，特征向量中心性算法的平均性能比CLDAG算法好39.55%。当正向种子节点为 300 个时，特征向量中心性算法和 CLDAG 算法分别可以正向激活 450 个和 318 个节点，并分别减少 383 个和 319 个负向影响激活的节点。当随机选择节点作为负种子集时，特征向量中心性算法的平均性能比 CLDAG 算法提高了 9.03%。 WM 数据集 2 的结果如图 29(c) 和 (d) 所示。当选择度最大的节点作为负种子集时，当从图中选择300个正种子时，特征向量

6. Summary and outlook

近年来，IBM问题得到了广泛的研究，并报道了许多有效的方法。在这篇综述中，我们简要回顾了IBM问题的最新研究进展。据我们所知，我们对 IBM 问题方法进行了最全面的研究，这些研究在方法数量和所采用的传播模型方面都已提出。这些方法已根据基于其理论方法的自定义分类法进行了分类。还描述和比较了支持特定 IBM 问题技术和影响传播模型的最重要结果。该综述为病毒传播、政府部门舆情管控、虚假信息管控、信息溯源等提供了理论支撑，也为社会经济发展安全稳定提供了有力的理论支撑和现实保障。我们希望这篇综述能够帮助来自不同背景的研究人员带来新的想法和见解。然而，IBM问题的进一步研究仍然存在挑战。 IBM 问题是一个相对年轻的研究领域，仍然存在许多开放的挑战。需要进一步的研究来理解为什么某些方法效果更好或比其他人更差取决于网络的属性。研究哪些特定的网络结构特性可以为每种技术带来更好的性能是一个开放的研究问题。此外，适应网络时间因素的技术很少，也没有适应网络动态变化结构的技术。在实践中处理复杂网络时的另一个主要困难是阻塞成本，这限制了可以应用的技术种类。因此，IBM未来研究的主要挑战是：

(1) More realistic and efficient diffusion models are needed

近年来，大多数关于 IBM 问题的研究都是基于节点以单一类型相互链接的网络。然而，在真实的网络环境中，用户之间可能存在多种类型的关系。例如，在社交关系网络中，人与人之间可能存在朋友、亲戚、同学等多种关系。在演员-导演-编剧-电影网络中，存在着合作、编剧和导演等关系。在引文网络中，存在协作和引文等关系。网络中的各种关系类型相互补充，传统的影响力传播模型已经无法描述这种多元关系网络。因此，如何为这些由多种关系类型的链接组成的多关系网络[237,238]设计影响力传播模型是值得研究的。此外，在当前的影响传播模型中，当正面和负面影响都到达网络中的节点时，该节点接受它们的概率不会随时间变化。然而，在真实情况下，个人接受积极或消极影响的概率可能会因许多复杂的社会因素而异。例如，在商品推销中，涉及商品的属性包括价格、性能、外观、品牌等，用户是否会购买该产品取决于他/她对这些属性的总体评价，例如，高价格的负面影响很难被接受。用户接受，品牌和性能的积极影响使得用户更容易接受产品。因此，如何融合节点的属性特征和网络拓扑特征也是未来值得研究的问题[61]。

(2) Consideration of the cumulative factors of negative influence

目前的研究都是在初始阶段进行影响抑制，与实际情况有些出入。在现实网络中，存在一种现象，在负面影响传播过程中，只有当被感染节点的比例达到一定阈值时，才会引起相关部门的关注，进而检测是否存在负面影响。影响网络中的谣言等节点。如果是负面影响节点，则启动相关策略进行压制或封锁。例如，谣言或病毒通常在初始阶段不会被压制。相反，在对谣言或病毒采取防控行动之前，它们可能已经传播到了一定阶段。因此，有必要考虑考虑负面影响的累积因素的IBM解决策略[239,240]。

(3) Influence of time factor on strategy design

现有的解决IBM问题的方法大多是基于在负面影响传播的初始阶段制定抑制策略，而没有考虑时间因素。然而，在现实世界的应用中，许多可预测和不可预见的事件随着时间的变化而发生：网络中节点之间的链接不断生成或删除，影响概率随时间变化，网络拓扑不断更新。例如，在社交关系网络中，朋友可能会变成敌人；随着时间的推移，同事可能会成为竞争对手。以前的策略没有考虑负面影响随着影响力传播而随时间的变化。此外，这些模型假设节点的状态在被负面影响激活后不再改变。然而，在现实生活中，每个节点的意图可能会随着时间而改变。例如，人们对政治活动或新闻事件的态度可能会随着网络的整体风向而改变[8]，其中负面种子的分布可能会随着时间的推移而改变。在这种情况下，需要实时修改阳性种子识别方法。因此，现有算法不能满足实时性要求，需要随着时间的变化采取更合理的抑制策略。例如，可以研究自适应抑制策略，以便在负面影响传播期间自适应调整策略，以优化资源和成本。

(4) Blocking the negative influence from uncertain sources

IBM现有的研究假设，当我们检测到正种子集来抵消负种子集时，负种子集，即负信息的来源，总是已知的。然而，在真实的社交网络中，很难知道负面影响的确切来源[150]。由于社交网络的隐私规则，很难确定社交网络中传播的谣言或错误信息的来源。很多情况下，我们只知道负种子的分布以及每个节点成为负种子的概率。负面影响源的分布用于描述负面种子的不确定性，可以通过经验知识或对用户行为的观察来估计。关于IBM不确定负源问题的研究相对较少。如何最大限度地防范不确定来源的负面影响也是未来研究的一个具有挑战性的课题。

(5) Integrating the heterogeneous data of multi-source influence

随着社交网络信息量的不断增加和网络结构的日益复杂，从多学科角度对网络影响力的传播机制和抑制最大化进行协作研究具有重要的理论意义。例如，在网络传播信息获取的研究中，舆情是由事件产生的，持续时间长、范围广。来自单一来源的数据已不能满足数据分析的丰富性、实时性、准确性的要求。此外，在多源数据的抓取、存储和处理过程中，由于数据标准的多样性和信息内容的重复，难以对多源异构数据进行分析。传统的数据处理技术无法满足从海量数据中快速提取关键信息的需求。而且原始数据缺乏明确的含义，多源数据之间往往难以集成和共享。因此，为了增强异构资源之间的互操作性，可以利用人工智能、大数据等最新的跨学科技术对数据进行标注，进行信息描述，满足协同数据交互的需求。

(6) IBM problems under cost constraints

疫苗是全球抗击流行病传播的有力工具。越多的人能够越早接种疫苗，国家就能越快地控制疫情并避免病毒广泛传播。然而，在一些发达国家大量储备疫苗的同时，大多数发展中国家却陷入严重的疫苗短缺。在COVID-19疫情依然严重、各种变异毒株给全球抗疫增添更多不确定性之际，疫苗是抗击疫情的关键。世界卫生组织表示，COVID-19 在全球的传播速度比疫苗的分发速度还要快。这个问题在发展中国家尤其是非洲国家尤为严重。疫苗分发问题，即如何以有限的成本最大限度地抑制疫情的传播，也是IBM应用未来研究的重要领域。总之，考虑到 IBM 问题在许多应用中的重要性，它仍然是许多开放研究问题。预计在不久的将来将提出具有更好准确性和性能权衡的新技术。

这篇关于Influence blocking maximization on networks: Models, methods and applications的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！