本文主要是介绍Influence maximization on temporal networks: a review，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Abstract
影响力最大化（IM）是网络科学中的一个重要主题，其中选择一个小的种子集来最大化网络影响力的传播。最近，这个问题引起了网络结构随时间变化的时间网络的关注。这种动态变化的网络上的 IM 是本次评论的主题。我们首先将方法分为两个主要范式：单播种和多播种。在单次播种中，节点在扩散过程开始时激活，大多数方法要么有效地估计影响力扩散并使用贪婪算法选择节点，要么使用节点排名启发式。在多重播种问题中，节点通过顺序播种、维护播种或节点探测范例在不同时间点激活。在整个审查过程中，我们特别关注在实践中部署这些算法，同时还讨论了实际应用程序的现有解决方案。最后，我们分享了未来的重要研究方向和挑战。
索引术语——图表；扩散;动态网络
1 INTRODUCTION
网络或图形是一种简单的工具，用于抽象地表示涉及交互实体的系统，其中对象被建模为节点，它们的关系被建模为边。由于网络的通用性和灵活性，过去几十年来许多现实世界的环境都利用了网络，包括：在线社交网络 [1]、[2]、[3]、基础设施网络 [4]、[5]、[6]和生物过程网络[7]，[8]。最近，人们不仅对理解网络的拓扑结构，而且对信息如何在网络上传播产生了极大的兴趣[9]、[10]、[11]、[12]。例如，在社交网络中，我们可能有兴趣了解人群中的病毒爆发，或在线环境中的突发新闻传播。
网络科学和机器学习应用于图的最基本假设是网络结构产生网络系统的功能。这一假设首先由 Georg Simmel 在 1890 年代以抽象术语进行讨论 [13]，并由 Jacob Moreno 和 Helen Jennings 在 1930 年代以图论语言进行讨论 [14]，这一假设接近核心结构主义——20 世纪的支柱（主要是社会）科学。这表明我们可以根据节点在网络中的位置来推断节点的功能。
基本功能概念是节点的重要性。但为了实施像重要性这样的概念，我们必须考虑有关系统的许多细节。一些问题可能包括：该系统的目标是什么？什么动力对其起作用？或者有哪些可能的情况-干预措施？影响最大化 (IM)1 假设这样一种情况：网络上可能会发生一些扩散（在数学和物理文献中，也称为传播）过程，并且我们希望该过程到达尽可能多的节点。这个扩散过程是由一些种子节点触发的，IM问题是识别使受扩散影响的节点数量最大化的种子节点。
病毒式（或口碑式）营销是一个明显的潜在应用领域，符合上述假设[15]、[16]、[17]、[18]、[19]。推荐系统是另一个相关的应用领域[20]、[21]、[22]、[23]、[24]，传播公共卫生运动也是如此[25]、[26]、[27]、[28]。然而，通过类比网络中心性（重要性术语下的另一个概念化家族），影响力最大化对于更广泛的问题领域很有趣。保护关键基础设施 [5] 或防范生物恐怖主义 [29] 也可以从影响力最大化研究中受益。对于不同但相关的场景，例如疫苗接种问题 [31]、[32]（找到其移除将尽可能有效地阻碍扩散事件的节点）和哨点监视 [33]、[34]，这也是一个可能的近似值 [30]。 ]（识别适合探针的节点，以早期可靠地检测扩散事件）。
肯佩等人。 [35] 在他们的开创性工作中首次提出了 IM 问题，从那时起，该问题就在计算机科学、统计物理学和信息科学文献中得到了广泛的探讨。大多数工作考虑节点和边固定的静态网络[35]、[36]、[37]、[38]。大多数方法要么有效地模拟影响力扩散函数，要么使用一些启发式方法按重要性对节点进行排名。我们避免对静态 IM 问题进行扩展讨论，而是让感兴趣的读者参考 [39]、[40] 中的评论。在许多现实世界的情况下，静态假设被违反，因为网络具有时间变化，链接形成和消失[41]。本次评论的主题是此类动态变化网络的 IM 技术和分析。例如，在 Meta 的 Facebook 或 Twitter 等社交媒体平台上，用户除了更新他们的联系之外还不断加入该平台。因此，为了实现令人满意的影响力传播，研究人员必须考虑这些动态。
IM 问题存在几个相关的关键挑战。首先，对于许多模型来说，简单地计算预期影响力传播是#P-hard的[38]。规避此问题的一种常见方法是蒙特卡罗（MC）模拟，其中对扩散过程进行大量模拟，并使用影响节点的平均数量来估计影响扩散[35]、[42]。尽管如此，选择最佳种子节点仍然是 NP 困难的[35]。因此，许多研究人员采用启发式方法，因此很难保证找到全局最优解。在时间网络中，边缘集动态变化和扩散过程的相互作用带来了额外的挑战。
在这项工作中，我们对时间网络 IM 的现有文献进行了全面的回顾，并阐明了未来的重要研究领域。本次审查的一个主要贡献是我们敏锐地关注与在实践中部署这些方法相关的挑战。虽然对静态和时间 IM 问题进行了大量研究，但我们发现“在现场”使用这些方法的研究很少。因此，我们强调每种方法对从业者的实用性。这将当前的工作与[43]和[44]中的评论区分开来。此外，[43]侧重于影响分析而不是严格的影响最大化，我们还讨论了作者未提及的几个任务，例如顺序播种和事前设置。
以下是本次审查的四个主要部分。在本节的其余部分中，我们将介绍研究 IM 问题的必要先决条件。在第 2 节中，我们讨论“单种子”方法，该方法在扩散过程开始时选择单个种子集。这个问题是静态IM问题的自然延伸。我们将现有方法分为三类，同时还讨论了分析扩散过程的方法。第 3 节的主题是随着网络演化重复选择种子节点的方法。在这一类别中，一些方法在整个扩散过程中的不同时间激活节点，而另一些方法“维护”有影响力的种子集。此外，我们还考虑节点探测问题，其中网络的未来演化只能通过探测一小部分节点来了解，并且这个部分可见的网络用于 IM 播种。请参阅图 1，
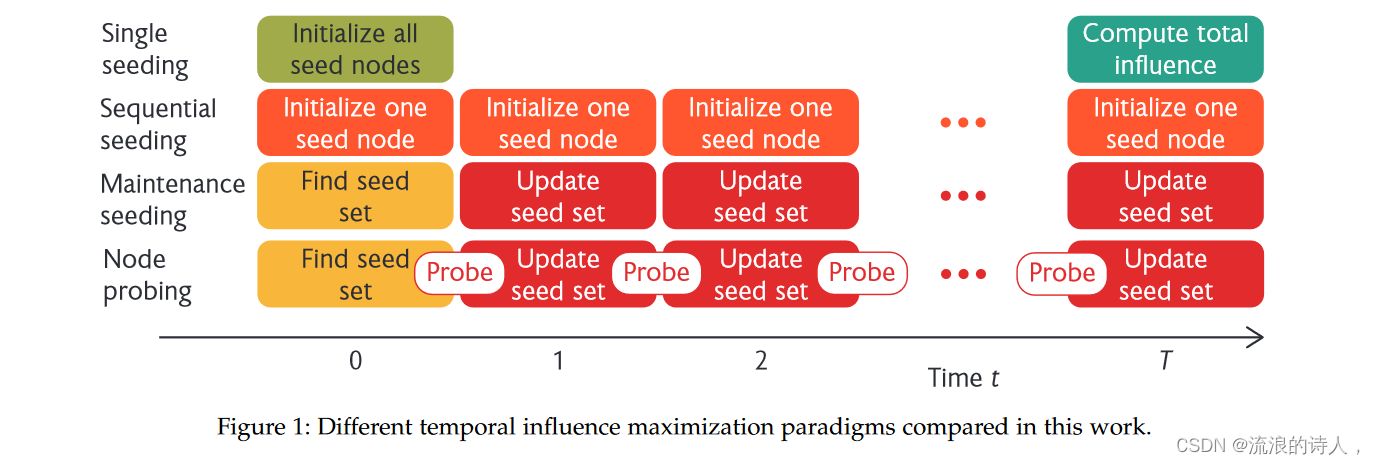图 1：本工作中比较的不同时间影响最大化范例。
了解比较这些不同范例的概述。 IM 算法的实际实施是第 4 节的主题，我们主要关注提高无家可归青少年的艾滋病毒意识的问题。该应用程序强调了与部署 IM 算法相关的许多挑战。最后，我们在第五节中总结了未来研究的重要领域，包括事前设置、模型错误指定以及扩散过程和网络演化之间的时间关系。在整篇论文中，我们特别关注这些方法在现实问题上的功能。
1.1 Notation
我们首先定义整篇论文中使用的常用符号。令 G = (G0, ..., GT −1) 为在 T 个时间戳上的时间演化网络。通常，图快照 Gt 出现在均匀间隔的时间间隔内，即 tk − tl 对于所有 k、l 都是恒定的。对于每个 t，令 Gt = (Vt, Et)，其中 Vt 是顶点集，Et 是边集。通常，Vt ≠ V 并且不随时间变化。令 n = | ∪t Vt|且 m = P t |Et|分别是网络中节点和边的总数。另外，令 Aij(t) 表示图 Gt 的相应邻接矩阵，其中如果在时间 t 存在从节点 j 到节点 i 的边，则 Aij(t) = 1，否则为 0。在无向网络中，对于所有 i、j，Aij = Aji，而对于有向网络，A 可能是不对称的。令 Ni(t) 为节点 i 在时间 t 的传入邻居集合，即 Ni(t) = {j : Aij(t) = 1}。
1.2 Diffusion mechanisms
为了研究 IM，有必要描述网络上影响力的扩散。最常见的扩散模型是独立级联 (IC)、线性阈值 (LT) 和易感感染恢复 (SIR) 模型。在 IC 模型 [35]、[45]、[46] 中，受影响的节点有一次机会激活其不受影响的邻居。具体来说，令 pij 为节点 i 影响节点 j 的概率。如果节点 i 是如果节点 j 在时间 t − 1 被感染，则节点 j 在时间 t 被感染的概率为 pij，假设 Aij(t − 1) = 1。从时间 t 开始，节点 i 无法再影响其邻居。那么总影响力传播就是任意时刻活跃的节点数量。
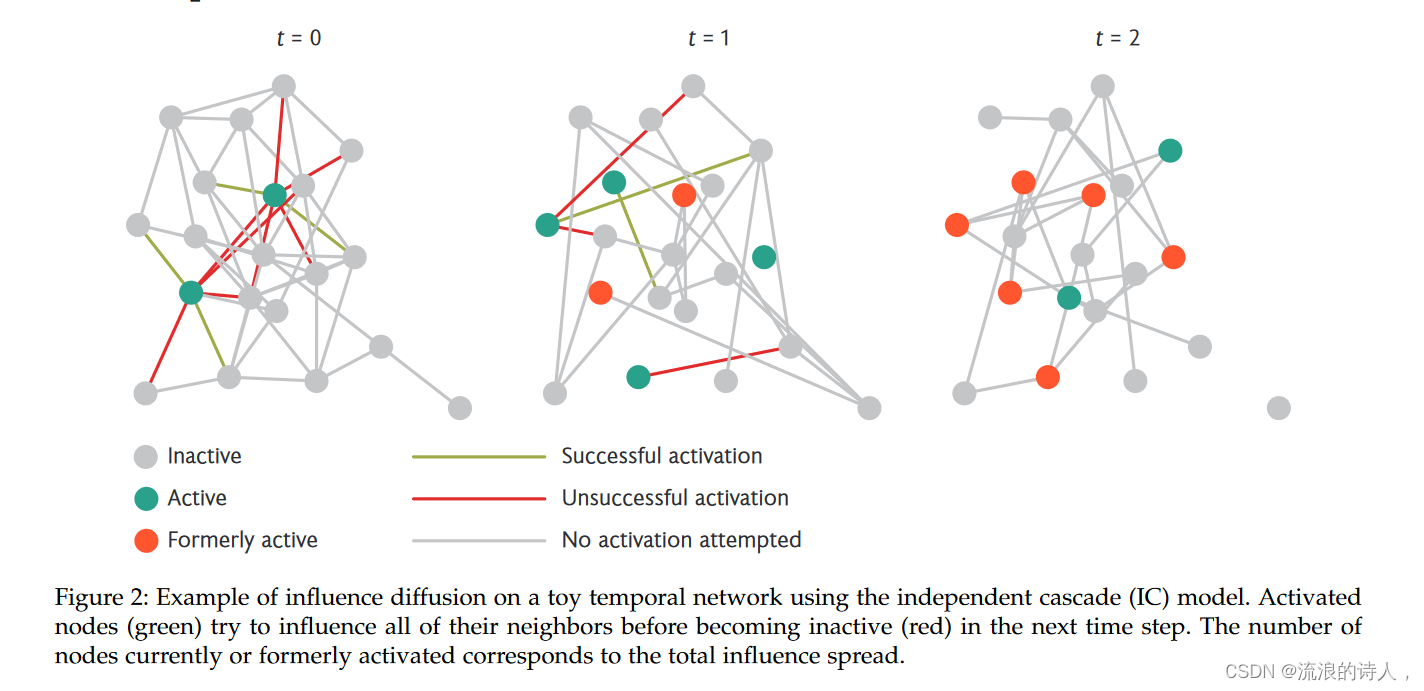
图 2：使用独立级联 (IC) 模型对玩具时间网络进行影响扩散的示例。激活的节点（绿色）尝试影响其所有邻居，然后在下一个时间步骤中变为不活动（红色）。当前或以前激活的节点数量对应于总影响力传播。
在图 2 中，我们使用 IC 模型展示了玩具网络上的影响扩散过程。最初选择两个节点（绿色）作为种子集并开始处于活动状态。这些节点尝试激活其所有邻居，但只有一些尝试成功（绿色和红色边缘分别表示成功和不成功的激活）。在下一个时间步中，新激活的节点现在尝试影响其当前的所有邻居，而先前激活的节点则变为不活动。此过程再继续一个时间步骤，处于活动（绿色）或以前活动（红色）状态的节点数量就是该种子集（八个节点）的总影响力传播。由于该过程的随机性，即使使用相同的种子节点重复该过程，总扩散扩散也可能不同。
SIR模型[47]、[48]与IC模型类似，但现在每个激活的节点都有固定的概率λ感染其未激活的邻居。此外，只要节点处于感染状态，就可以激活其邻居。然而，每个受感染的节点都有“恢复”并且无法激活其邻居的概率 μ。总影响力传播是最终处于感染和恢复状态的节点数量。如果对于所有 i、j 和 μ = 1，pij = λ，则 SIR 和 IC 模型是等效的。此外，如果 μ = 0，SIR 模型会简化为易感感染 (SI) 模型 [49]、[50]。
在LT模型[35]、[46]、[51]、[52]中，每个节点被随机分配一个阈值θi，每条边被赋予一个权重bij。如果节点受感染邻居的权重总和超过其阈值，则该节点将被感染，即，如果 P bij > θi，则节点 i 被激活，其中总和涵盖 i 的所有受感染邻居。
1.3 Problem statement
有了符号和扩散机制，我们正式定义了 IM 问题。令 G 为某个动态网络，令 D 为扩散机制，例如 IC 或 SIR。我们将 σ(S) 定义为种子集 S 和图 G 上的扩散过程 D 受影响节点的预期数量。我们抑制 G 和 D 对 σ(·) 的依赖性，但强调其行为高度依赖于两者。对于固定的 k = |S|，我们寻找最大化 σ(S) 的种子集 S，即
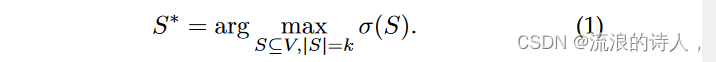
也许近似 (1) 的最简单方法是通过 MC 模拟评估 σ(S) 并选择在影响力传播中产生最大收益的节点，如算法 1 中所述。在静态设置中，这种贪心算法可证明会产生结果在全局最优值的 (1 − 1/e) 范围内 [35]。然而，MC 模拟的计算量很大，因此许多方法都专注于在采用贪心算法之前有效计算影响范围。
另一种避免直接计算影响函数的选择种子节点的常见范例是基于节点排名。根据某种重要性度量（例如程度或中心性）对节点进行排名，并选择具有最大值的 k 个节点作为种子集。虽然比贪婪算法快得多，但这些方法产生了没有理论保证，并且可能选择与其影响力“重叠”的节点。例如，如果两个节点具有高度但共享许多公共邻居，则为两个节点播种可能不是最佳的，因为它们的影响将传播到相同的节点。
反向可达 (RR) 草图还选择种子节点，而不直接计算 σ(S)。对于给定时间 t 和每条边 (i, j)，我们随机绘制 Zij ∼ Bernoulli(pij)，其中 pij 是节点 i 影响节点 j 的概率，并保持子图 Zij = 1。这些边有时被引用作为“活动”或“活动”边缘。一旦构建了该子图，在随机选择节点之前，每个（有向）边的源和目的地都会反转。最后，从这个随机选择的节点开始进行广度优先搜索，并且为这个特定的 RR 草图保留该搜索到达的所有节点。本质上，该集合中的节点是那些可以通过扩散过程影响所选节点的节点。该过程重复多次以产生一组 RR 草图。
2 SINGLE SEEDING
经典的 IM 问题是从业者在时间 t=0 时选择一组种子节点，以便在时间 t=T 时最大化影响力传播。大多数解决方案要么通过概率估计影响力传播，要么使用一些启发式方法按影响力对节点进行排名。对于大多数这些方法，假设网络的完整时间演化是已知的，但有些方法放宽了这一假设。我们还讨论了一些不提出新颖算法，而是分析现有方法和/或扩散过程的作品。
2.1 Algorithms
首先，我们讨论解决单种子时间 IM 问题的算法。
2.1.1 Greedy
Kempe 等人的贪婪算法。 [35] 自然地扩展到时间设置：影响力传播中边际收益最大的节点被增量地添加到种子集中，如算法 1 所示。与 [35] 的唯一区别是，预期影响力传播是根据时间演化计算的网络。该方法被认为是 IM 算法的“黄金标准”，可以轻松适应任何扩散模型。另一方面，由于计算影响力分布需要重复的 MC 模拟，该算法的计算成本很高。
2.1.2 Probability of influence spread
由于贪心算法的昂贵步骤是计算影响力扩散，因此存在几种启发式方法，它们使用节点激活的概率来近似 σ(S)。在阿加瓦尔等人中。 [53]，πi(t)是节点i在时间t被激活的概率。假设网络是一棵树，如果 pji(t) 是节点 j 在时间 t 激活节点 i 的概率，则节点 i 在时间 t + 1 激活的概率为
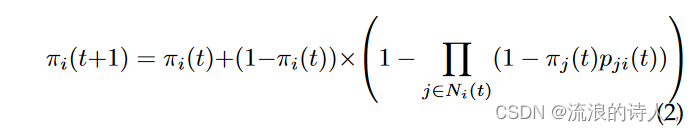
其中 Ni(t) 是节点 i 在时间 t 的传入邻居的集合。第一项是节点在前一个时间步中已被激活的概率，而第二项是节点之前未激活但在当前步骤中激活的概率。如果 i ∈ S，作者初始化 πi(1) = 1，否则初始化 0。对于每个 i，πi(t) 通过 (2) 迭代更新，并且 P i πi(T ) 估计 σ(S)。阿加瓦尔等人。使用此过程和贪心算法来选择种子集。作者假设 pij(t) 是节点 i 和 j 之间的边持续存在的时间长度的增函数。此外，该方法避开了标准的等间距图形快照，而是采用与基于边更新数量的结构变化相对应的时间。该方法还可以找到给定扩散模式最可能的种子节点。
Osawa 和 Murata [49] 采用了与 Aggarwal 等人类似的方法。但使用SI模型进行扩散。事实上，如果对于所有 i、j 和时间 t，pij(t) = λ，则该方法等效于[53]。 Osawa 和 Murata 证明这种方法稍微高估了真实的影响力扩散，并证明相关的贪婪算法的计算复杂度为 O(nmk)。在模拟中，该方法优于广播[54]和接近中心性[41]启发法。它还产生与标准贪婪算法相当的性能，但速度快两个数量级。此外，Osawa 和 Murata 表明，由于节点影响力重叠，中心性启发法在具有强大社区结构的网络上表现较差。
埃尔科尔等人。 [55]将此范式扩展到SIR模型。如果 πi(t) 定义如上，并且 ρi(t) 是节点 i 在时间 t 处于状态 R 的概率（这样 1 − πi(t) − ρi(t) 是处于状态 S 的概率） ，那么 SIR 动态定义为
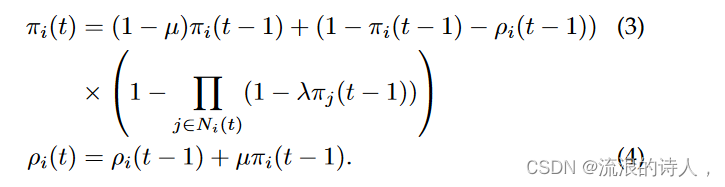
贪心算法根据影响力分布估计 P i{πi(T ) + ρi(T )} 选择种子节点。埃尔科尔等人。研究当网络有噪声或不完整时该方法的性能，即时间快照随机重新排序，只有第一个快照可用，并且网络聚合为单个快照。作者发现快照的顺序至关重要，对 G1 的无知会导致算法受到影响。事实上，在许多情况下，仅了解 G1 就足以实现较大的影响力传播，而聚合方法始终表现不佳。埃尔科尔等人。还表明，如果 μ 较大，则前几层的中心节点是最佳影响传播者，而对于较小的 μ，节点必须位于许多层的中心才能获得最佳种子节点。
2.1.3 Node ranking heuristics
除了估计影响力传播之外，以下方法还根据影响力对节点进行排序，并选择前 k 个作为种子节点。最早的方法来自 Michalski 等人。 [56]。作者采用LT模型并假设前T/2个快照可用于选择种子节点，但是扩散过程发生在 GT/2, 上。 。 。 ，GT-1。为所有节点 i 和快照 Gt 计算节点重要性 mi(t) 的一些静态度量。通过降低旧值的权重来组合 t 上的值，以生成每个节点的单个度量 θi，即
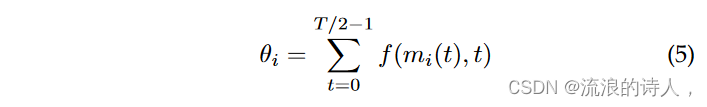
其中 f (x, t) 是 t 中的增函数。对于给定的 f (·)，选择具有最大 θi 的 k 个节点作为种子节点。米哈尔斯基等人。发现度量 mi(t) 和遗忘机制 f (·) 的以下组合产生最大的影响范围：指数遗忘的出度和入度 (fexp(x, t) = e−tx)2，总度和对数遗忘 (flog(x, t) = logT/2−1−t+1(x))，介数中心性和双曲遗忘 (fhyp(x, t) = (T /2 − 1 − t − 1)− 1x）；以及具有权力遗忘的紧密中心性 (fpow(x, t) = xt)。作者还改变了用于计算指标的聚合快照的数量，并发现最细的粒度表现最好。事实上，通过聚合 G0，将网络视为静态网络。 。 。 , GT/2−1 到单个图中产生对 GT/2, 的影响最小。 。 。 ，GT −1，从而证明了考虑网络中时间变化的重要性。
另一个节点排名启发式来自 Murata 和 Koga [50]。使用 SI 模型，作者将几个重要的静态测量扩展到时间设置。特别是，动态度折扣算法扩展了[37]。首先，将动态度最大的节点DT(v)添加到种子集中，其中
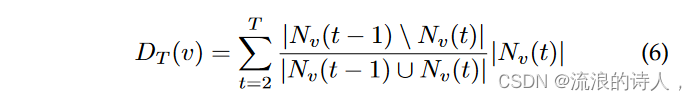
Nv(t) 是节点 v 在时间 t 的邻居。一旦一个节点被选择，其邻居节点的动态度值就会减小，并且重复该过程直到选择k个节点。作者表明，该方法的复杂度为 O(k log n + m + mT /n)，但仅对 SI 模型有效。 Murata 和 Koga 还提出动态 CI 作为基于最优渗流的 [57] 的扩展，以及动态 RIS 作为基于 RR 草图的 [58]、[59] 的扩展。在模拟中，所有方法的性能与 Osawa 和 Murata [49] 相当，但速度明显更快。作者还表明，当 λ 很大时，选择最佳种子节点就不那么重要了，因为许多种子集产生的影响力分布相当。
最近，[60]提出了另一种节点排序启发式。作者假设，对于 IC 模型，应选择其邻居具有较大变异性的节点以最大化传播。他们使用熵度量来量化邻域变异性，该熵度量奖励在后续图快照中更改其邻居的节点，并选择具有最大值的 k 个节点作为种子集。该度量是在第一个 T /2 快照上计算的，而影响是在图的后半部分演化中计算的，类似于 Michalski 等人。 [56]。作者指出，然而，这个指标对于 LT 模型可能没有意义，LT 模型需要“积累”激活邻居的数量才能使节点受到感染。由于该方法依赖于每个节点的邻域集，因此其复杂度为O(m)。
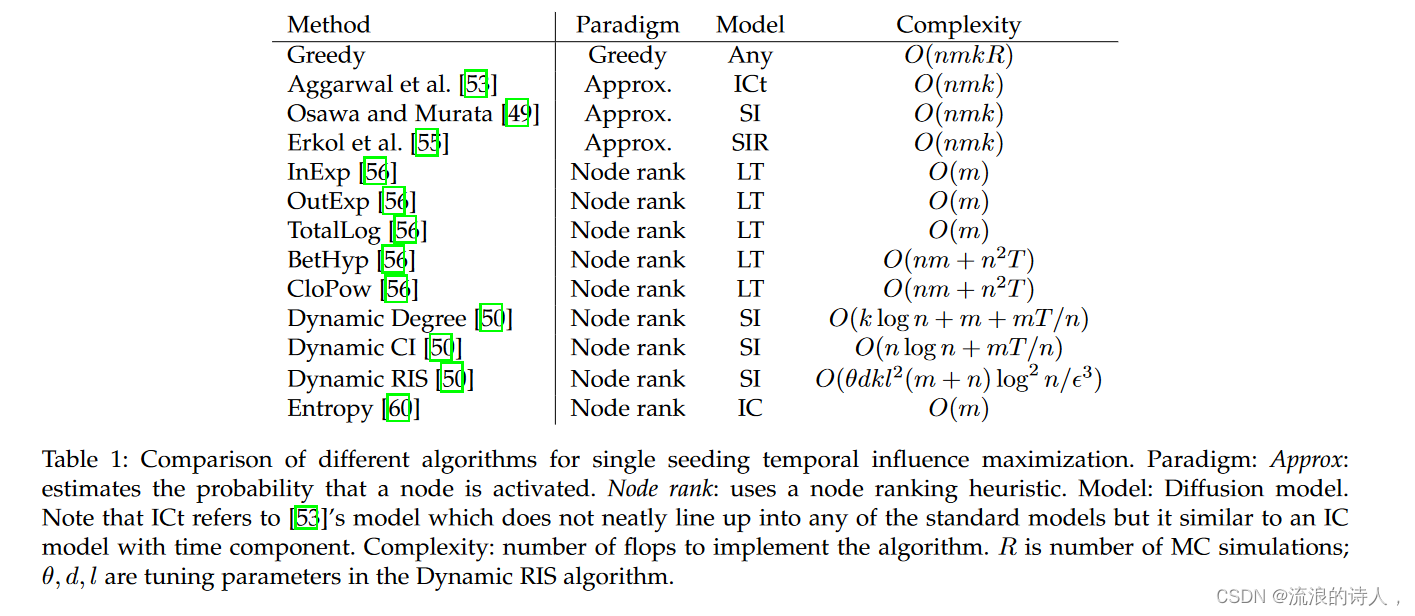
表 1：单播时间影响最大化的不同算法的比较。范式：Approx：估计节点被激活的概率。节点排名：使用节点排名启发式。模型：扩散模型。请注意，ICt 指的是 [53] 的模型，它并不完全符合任何标准模型，但它类似于具有时间分量的 IC 模型。复杂度：实现算法的触发器数量。 R是MC模拟的次数； θ、d、l 是 Dynamic RIS 算法中的调整参数。
为了总结前两小节中的方法，我们在表 1 中对它们的几个指标进行了比较。
2.2 Analysis
我们将注意力转向不提出新颖的 IM 算法，而是分析现有算法和/或扩散机制的方法。为了更好地模拟信息传播，Hao 等人。 [61]提出了两种新颖的扩散模型，其中节点的激活倾向取决于过去尝试激活它的次数。在时间相关的综合级联模型中，活动节点仍然只有一次机会激活其邻居，但被感染的概率可能会增加、减少或不受该节点先前尝试次数的影响。作者还提出了一种动态 LT 模型，其中节点的激活阈值取决于之前激活尝试的次数。郝等人。提出了一种基于时间序列的方法来凭经验确定过去的激活尝试对感染概率的影响。
盖罗等人。 [62]研究了几种新颖的扩散模型下影响扩散函数的行为，同时也允许种子节点在不同的时间被激活。令 f : 2V → R 为集合函数。如果 S ⊆ V ，则 f (S∪{v})−f (S) ≥ 0 对于所有 v ∈ V \S 且 S ⊆ V ，则 f 是单调的。如果 f (A ∪ {v}) − f (A) ≥ f (B ∪ {v}) − f (B) 对于 A ⊆ B 且 v ∈ V \ B，则它是次模的。换句话说，单调性质意味着添加节点永远不会减少影响力传播，而子模块性意味着添加更多节点的收益递减。此外，如果所有节点都应在时间 t = 0 时激活，作者将播种策略定义为对时序不敏感，否则对时序敏感。在瞬态演化 IC 模型 (tEIC) 中，时间 t − 1 的受感染节点有一次机会在时间 t 感染其邻居。作者证明这种扩散机制既不是单调的也不是子模的。与 tEIC 模型相反，持久 EIC 模型假设一个节点在两个节点第一次建立链接时尝试激活其邻居。如果激活概率随时间恒定，Gayraud 等人。证明该模型是单调的、子模的且对时间不敏感的。如果激活概率动态变化，则影响函数既不是单调的也不是子模的，并且是时间敏感的。作者提出了对 LT 模型的类似扩展。瞬态 ELT 模型仅考虑当前快照中活动邻居的权重，而持久 ELT 模型则将之前任何时间激活的邻居的所有权重相加。这些模型分别是单调的、非子模的和时序不敏感的，以及单调的、子模的和时序不敏感的。本文的关键贡献在于，如果模型对时间敏感，则应在整个扩散过程中激活种子节点，而不是在 t = 0 时全部激活。作者还表明，基于聚合所有图快照来选择种子节点并不需要对于任何模型都表现良好。
[48] 中也研究了影响函数的子模性，这次是在 SIR 模型下。作者表明，如果 μ = 0（SI 模型），则影响函数是次模的，但当 μ > 0 时，就会失去此属性。实际上，违规行为来自状态 R 中的节点，“阻塞”到状态 S 中的节点的路径，
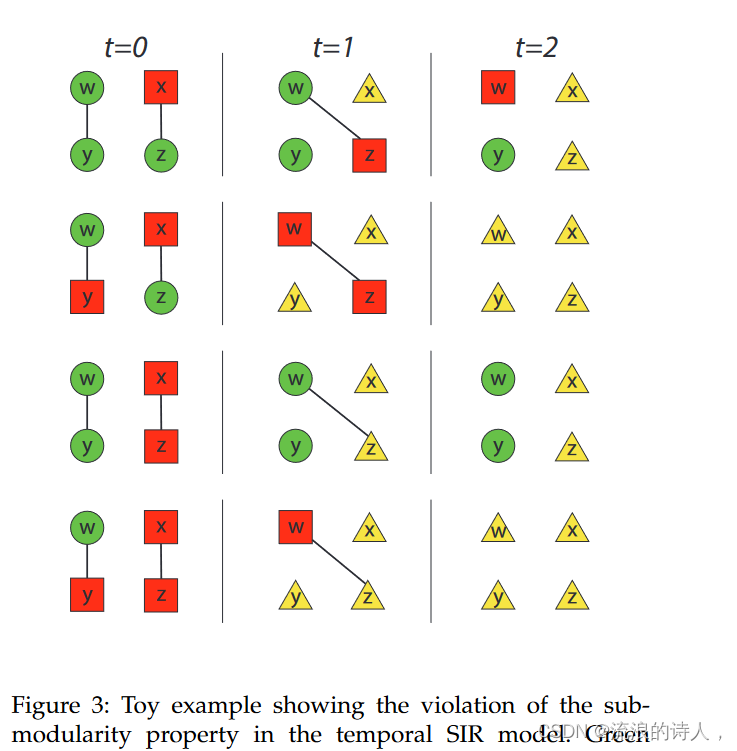
图 3：显示违反时间 SIR 模型中子模属性的玩具示例。绿色圆圈是易受影响的节点，红色方块是受感染的节点，黄色三角形是恢复的节点。每行代表特定种子集的扩散过程，其中 λ = μ = 1。在第一行中，S1 = {x}，总影响力传播为三个节点。在第三行中，S2 = {x, z}，但总影响力传播只有两个节点。因此，S1 ⊂ S2，而 σ(S1) > σ(S2)。经作者许可转载自[48]。
如图所示通过图 3 中的玩具示例（经作者许可转载）。在 SIR 模型中也没有实现子模性质的松弛，即 γ 弱子模。如果 A ∩ B = ∅ 且 0 < γ ≤ 1，则函数 f 是 γ 弱子模，
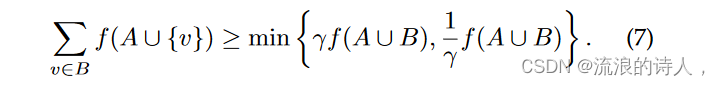
然后，作者根据经验检查了实际网络中违反子模块标准的数量。他们发现，如果随机选择节点，则经常会违反标准。然而，如果基于贪婪算法选择节点，则很少会违反子模块性属性。因此，影响函数实际上是子模的。现在，由于影响函数不是子模的，因此无法从理论上保证贪心算法充分逼近最优解。尽管如此，与现实世界网络上的暴力算法相比，贪心算法的结果仍然在最优解的 97% 以内。
最后，虽然与 IM 没有明确相关，但我们还是简要讨论了[63]。这项工作通过分析扩散的哪一部分归因于扩散机制、哪一部分归因于图动力学，研究图拓扑演化与扩散过程之间的关系。作者考虑了两种计时机制：基于交互之间秒数的外部时间，以及基于网络变化或转换的内部时间。虽然研究人员通常使用外部时间，但作者认为在许多情况下内部时间可能更明智。使用 SI 模型和固有时间，观察到的扩散更多地受扩散机制而非网络演化的控制。相反，使用外部时间，网络中的拓扑变化极大地影响扩散。就这样扩散过程高度依赖于计时方法。
2.3 Discussion
在前面的小节中，我们介绍了在时间 IM 中选择单个种子集的主要方法。每种方法要么估计影响力传播，要么根据启发式对节点进行排名。阿加瓦尔等人。 [53]、Osawa 和 Murata [49] 以及 Erkol 等人。 [55]提出了类似的方法，唯一的区别在于扩散模型。这些方法保留了贪婪算法的许多所需属性，但计算强度较低。 [56]、[50]和[60]的节点排名指标甚至更快，因为它们避免了昂贵的影响力传播计算。理论上，这些方法不能保证与基于贪婪的算法一样好，但例如[50]表明它们仍然保持良好的性能。
在解决现实问题时实施这些方法的一个关键挑战是要求知道网络的整个拓扑。保存[56]，[60]，每种方法都假设网络的演化G0，. 。 。 , GT −1 在选择种子节点时的时间 t = 0 时已知。当然，在实践中，从业者知道网络的未来拓扑是不合理的，因此在这种情况下如何应用这些方法并不明显。为了解决这个问题，[64]提出了一种用于事前即时 IM 的链接预测方法。使用 SI 模型，作者使用前 p 个快照来训练链路预测算法，然后预测 Gp 的网络拓扑。 。 。 ，GT-1。将现有的时间 IM 算法应用于这些预测网络来选择种子集。在许多情况下，在 G0、. 的简单聚合上查找种子节点。 。 。 ，Gp−1 的性能与更复杂的链路预测方法一样好。这一发现与 Michalski 等人的观点不一致。 [56]和Erkol等人。 [55] 表现出 IM 算法在聚合网络上表现不佳。然而，这些论文假设了不同的扩散机制，因此聚合可能只适用于 SI 模型。应用研究人员的另一个实际考虑因素是网络的规模。如果使用相对较小的社交网络，那么贪婪算法是合理的，而对于具有数百万节点的大型在线社交网络，节点排名启发式是强制性的。最后，必须根据应用领域仔细选择扩散机制，因为某些方法仅适用于特定机制。
3 MULTIPLE SEEDINGS
在上一节中，我们考虑了时间网络的 IM 算法，其中所有种子节点在时间 t = 0 时被激活。现在我们讨论在整个网络演化过程中的不同点处播种节点的方法，或者在每个时间步
3.1 Sequential seedings
与单种子问题相关，考虑单个种子集 S，但不是在 t = 0 时激活所有节点，而是随着网络的发展节点依次激活。这个问题不仅涉及选择将哪些节点包含在种子集中，还涉及何时激活它们。
米哈尔斯基等人。 [65]重点关注这个问题的种子激活步骤。作者考虑了 IC 模型的一种变体，其中单个节点被激活，并且扩散发生，直到不再可能激活为止。然后激活下一个节点并继续该过程。在这种情况下，Michalski 等人。使用基于程度的简单种子选择方法。首先，度数最大的节点被激活。一旦扩散过程完成，度数最大的未感染节点将被激活，并且该过程将继续，直到 k 个节点被播种。该方法与在时间 t = 0 时激活度数最大的 k 个节点进行比较。当 t 很小时，一次激活所有节点会导致更大的影响力扩散，但随着 t 的增加，顺序播种策略优于单次播种，如下所示如图4所示（经作者许可转载）。
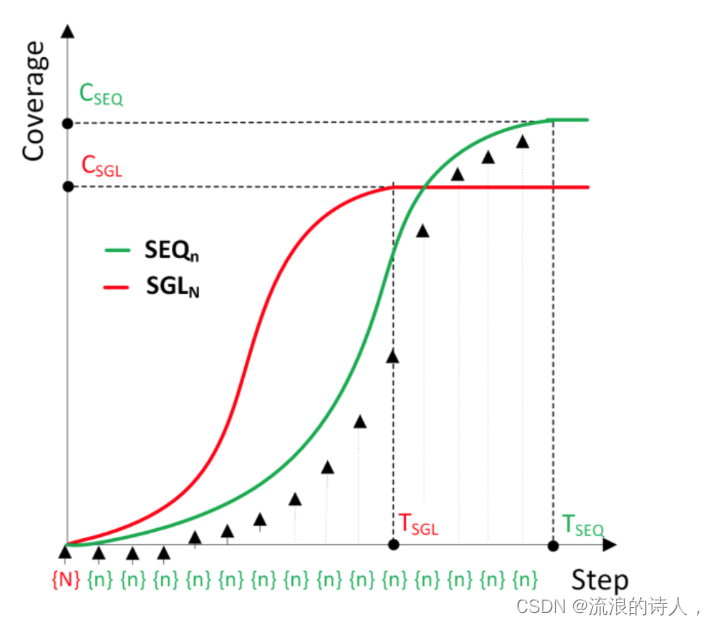
图 4：顺序播种策略与单次播种策略的影响扩散比较。红色曲线在 t = 0 时激活所有节点，而绿色曲线一次激活一个节点。单次播种首先会导致更大的影响力传播，但顺序播种策略最终会导致更大的影响力传播。经作者许可转载自[65]。
翁等人[66]考虑顺序播种问题的另一种变体，其中种子集节点以某种概率不成功激活。他们提出了一种贪婪算法，可以在给定当前扩散的情况下最大化影响力扩散的边际增益。为此，作者通过基于可能的种子集和传播概率构建具有额外节点和边的辅助图，得出了预期受影响节点数量的封闭式表达式。贪婪算法被证明可以在最佳影响范围的 (1 − 1/e) 范围内产生结果，同时通过惰性前向技术减轻计算负担 [67]。此外，Tong 等人。证明 Michalski 等人概述的策略。 [65]每次播种一个节点并在激活下一个节点之前等待扩散过程完成是任何时间图的最佳播种策略。
3.2 Maintenance seeding
在高度动态的网络中，最佳种子集可能会随着时间而变化。例如，在 Twitter 上的长期营销活动中，活跃用户和关注者会随着活动的持续时间而变化。因此，有必要维护或更新种子集St，以使其对所有t的Gt提供最大的影响范围。这个问题被称为维护播种。维护播种与静态播种明显不同，因为现在在每个时间步 t 激活 k 个节点，以便最大化 Gt 上的扩散。因此，这个过程类似于一系列静态 IM 问题。
陈等人。 [68]、[69]首先以“有影响力的节点跟踪”的名义研究这个问题。作者假设在下一个时间步 Gt+1 时网络拓扑已知，并使用 IC 模型进行扩散。使用当前快照的种子集 St，Chen 等人。采用交换启发式 [70] 来有效地更新种子集并证明解决方案保证在最佳分布的 1/2 范围内。实际上，该方法将 St 中的一个节点与 V \ St 中的一个节点交换，以最大化影响力传播的边际增益。由于评估 V \ St 中每个节点的边际增益成本很高，因此作者仅考虑具有最大边际增益上限的节点。如果节点 u ∈ V \S 的上限小于另一个节点 v 的边际增益，则无需评估节点 u 的影响力，因为它的包含不能改善总影响力分布。所提出的算法具有 O(kn) 复杂度。
奥坂等人。 [71]考虑大型在线网络的类似问题，其中在每个时间步添加或删除节点和边。使用 IC 模型，作者提出了一种类似于 RR 集的草图方法和一个有效的数据结构来构建和存储这些草图。然后实施贪婪算法来选择种子集。具体来说，选择出现在最多草图中的节点作为种子节点。然后，包含该节点的所有草图均被排除在外，并且选择出现在最多剩余草图中的节点作为种子集。这个过程一直持续到 k 个节点被选择为止。除了新颖的数据结构之外，这项工作还提出了启发式方法，可以在图的每次演化时有效更新草图，而不是从头开始重新计算它们。这些启发式方法具有理论保证并可提高算法速度
还有其他几种方法可以解决这个问题。 [72] 将其重新定义为强盗问题，但以与 Ohsaka 等人类似的方式解决它。通过使用 RR 草图。 [73] 在 t = 0 时找到最佳种子节点，并根据调查快照之间发生显着变化的图表部分来增量更新它们。 [74]基于滑动窗口方案选择种子节点，[75]使用节点的三角形数量来估计其影响。 [76]通过考虑在线社交网络中的用户属性来考虑特殊情况，包括首选的参与主题。作者还考虑了用户可能不活跃的某些时间段，并允许根据主题使用不同的传播模型。
到目前为止，每种方法都假设了解网络的未来拓扑。 [77]通过使用条件时间限制玻尔兹曼机[78]预测未来一个时间步的图结构，然后在预测图上找到种子节点，从而放松了这一假设。作者使用交换 [70] 启发式方法来更新种子集和 [69] 中的想法，以提高效率。
Peng [79]没有提出新的维护种子算法，而是研究摊销运行时间，即在每个时间步更新种子节点所需的时间。尽管当前的算法可以在每个 t 的 O(n) 时间内有效地更新种子集，但作者认为这对于大型网络来说仍然太慢。然后，Peng 考虑了 IC 或 LT 模型下的两种不同的图演化范式。第一种是增量模型，其中网络只能添加新的节点和边。在此模型下，Peng 表明，对于摊销运行时间 O(kε−3 log3(n/δ))，最优解的近似 (1 − 1/e − ε) 的概率为 1 − δ，比 O 快得多（n）。然而，在完全动态的模型下，节点和边可以添加和删除，作者证明，如果没有 n1−o(1) 摊销运行时间，2(− log n)1−o(1) 近似是不可能的。因此，不可能改进 O(n) 运行时间。
3.3 Node probing
虽然以前的方法假设完全了解未来的网络拓扑，但节点探测问题假设未来的图快照是未知的，但可以通过探测某些节点的邻域来部分观察。这里，探测节点意味着观察其边缘。假设 G0 已知，目标是仔细选择要探测的节点，以获得有关网络拓扑的最多信息，从而有效地实现 IM 算法。这个问题可能会出现在大型在线社交网络中，在这些网络中不可能在每个时间步骤观察所有用户的活动。另一个相关应用是对难以接触的人群（例如无家可归的年轻人）内的社会联系进行建模，因为没有直接的方法来观察该网络中的所有人（节点），但仅观察友谊（边缘）。
这个问题最初是由 Zhuang 等人提出的。 [80]。对于每个 t，研究人员探测 b 个节点并观察它们邻域的变化。一旦节点被探测到，IM 算法就会在（不完整的）可见网络上实现。因此，目标是找到理想的探测策略。作者提出了对 IM 问题的解决方案产生最大可能变化的探测节点。由于作者使用度折扣算法[37]，这减少了寻找度数变化最大的节点的过程。具体来说，令 β(v) 为探测节点 v 前后选择的最佳种子影响力传播的最大差异。此外，令 S 为时间 t − 1 时的最佳种子节点，令 S0 为具有最大影响力的 k 个节点。最新图表快照的入度。令 t − cv 为节点 v 被探测的最后一个时间戳。对于 ε > 0，如果 zv = √−2cv log ε，则 β(v) 推导为：
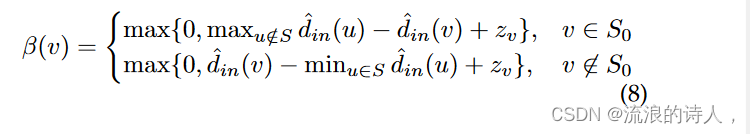
其中 ˆ din(v) 是基于最近探测的网络的节点 v 的入度。然后节点 v* = arg maxv∈V β(v) 被探测并更新网络拓扑。一旦探测到 b 个节点，就会应用度折扣算法来确定影响力传播的最佳种子节点。
韩等人。 [81]研究了同样的问题，但重点关注具有高变异性的社区而不是节点。作者假设，一个群落的总入度随着时间的推移应该是相对稳定的，所以如果这个变化很大，那么这个群落一定发生了重大变化，值得探讨。作者使用[82]的社区检测算法，一旦识别出具有高变异性的社区，他们就采用类似于 Zhuang 等人的探测算法。 [80]。
3.4 Discussion
我们通过强调实际实施这些方法的重要考虑因素来结束本节。在顺序播种设置中，研究人员必须考虑允许扩散发生多长时间，因为静态播种更适合小 T ，顺序播种更适合大 T 。米哈尔斯基等人。 [65]还强调顺序策略更适合独立激活的模型，例如IC和SI，而不是基于阈值的模型，例如LT，因此扩散模型是另一个重要的考虑因素。对于更复杂的 IM 算法，比较静态播种和顺序播种也很有趣。众所周知，播种前 k 度节点是一种相对较差的 IM 算法，因此尚不清楚顺序播种与不同 IM 算法结合时是否会表现得更好。
对于维护播种，我们观察到播种预算实际上是 kT 而不是 k，因为 k 个节点在 T 个不同的时间步被激活。如果 T 很大，那么每轮持续激活 k 个节点可能会被禁止。此外，此设置隐式假设节点可以在连续快照中重新感染，即 St ∩ St+1 ̸= ∅。这在流行病学环境中可能是合理的，例如，一个人可能被某种疾病再次感染。另一方面，对于营销活动来说，在多个时间步骤中以广告为目标的用户不太可能在每种情况下都有显着的传播。因此，应仔细考虑用户被感染的次数以及对传播机制的影响。此外，保存 IC 模型，如果一个节点在时间 t 被感染，那么它可以在 t + 1、t + 2 时继续尝试感染其邻居。 。 。 。然而，上面提出的框架假设除非节点位于新的种子集 St+1 中，否则它们无法施加影响。接下来，保存[77]，每种维护播种方法都假设未来的网络拓扑是已知的，这在实践中通常是不真实的。特别是，当图快照未知时的顺序播种策略是一个重要且实际相关的开放问题。最后，杨等人。 [83]认为识别有影响力的节点是与影响力最大化不同的任务。例如，如果新用户加入 Twitter，他们可能想关注最有影响力的用户。识别这些用户与试图在 Twitter 网络上最大限度地传播产品或想法不同。
节点探测问题是迈向实际相关 IM 算法的有希望的一步。事实上，假设网络结构是未知的，除非通过探测，比假设完整拓扑信息的方法要现实得多。然而，这些方法将问题视为一系列静态 IM 任务，因为种子节点是在每个时间步骤中重新计算的。一个有趣的进步是利用之前的种子集来计算新种子。
4 REAL WORLD IMPLEMENTATIONS
本次审查的一个重点是了解现有方法是否准备好处理“现场”的 IM 任务。迄今为止，有关现实环境中即时通讯的文献还很少。在本节中，我们重点介绍现有的研究并讨论一些相关的挑战。虽然这些工作假设网络是静态的，但大多数都采用顺序播种策略，这就是我们将其包含在时间 IM 的讨论中的原因。据我们所知，目前还没有明确在动态网络上实现 IM 算法的论文。
应用 IM 最著名的例子来自 Yadav 和 Wilder 的一系列论文 [25]、[26]、[27]、[28]、[84]。这些工作的目标是最大限度地提高大城市地区无家可归青年对艾滋病毒的认识。这是一个经典的即时通讯设置，因为无家可归者收容所只能对少数青少年进行艾滋病毒预防培训，但希望参与者将这些信息传递给他们的朋友，以最大限度地提高认识。一般问题设置如下。首先，流浪青少年的社交网络初步构建。然后无家可归者收容所选择 k 名青少年参与艾滋病预防干预。训练期间，青年们一一吐露了所有的友谊。然后，在邀请 k 个更多的年轻人参加培训之前，信息会被给予时间在网络上传播（但这种传播是未知的）。此过程将持续进行 T 轮训练。
在此环境中部署 IM 算法存在几个关键挑战。首先，无家可归青年群体的完整社交网络无论是节点（青年）还是链接（友谊）都是未知的。此外，随着青少年的训练和他们的友谊圈的阐明，实验过程中收集了有关网络结构的新信息。其次，年轻人可能会拒绝和/或无法参加培训，这意味着种子节点有一定的概率保持不活跃状态。最后，量化网络上传播的信息非常重要。因此，这个问题结合了节点探测（因为在选择节点来了解其社交圈之前网络结构部分未知）和顺序播种（其中节点随着时间的推移而被激活）。然而，它与标准节点探测问题的不同之处在于，选择节点是为了优化影响力传播，而不是最大化网络的拓扑信息；它与顺序播种的不同之处在于，选择下一个种子节点时影响范围是未知的
解决这些挑战的第一次尝试来自[25]。假设扩散采用 SI 模型3，作者使用 Facebook 友谊构建社交网络，同时使用链接预测技术推断丢失的链接 [85]。他们证明，在每个 T 时间步选择 k 个种子节点的任务是 NP 困难的，并且不可能通过不确定的网络实现最优解的 n−1+ε 近似。然后问题被重新构建为部分可观察马尔可夫决策过程（POMDP）。通过模拟扩散过程，选择具有最大预期奖励（影响力扩散）的节点作为种子集。为了使该方法能够处理现实世界的网络规模，作者提出了一种分而治之的方法。他们提出的方法比现有方法快一百倍，同时还产生更大的影响力传播。在[25]中，作者通过允许影响和边缘概率更大的不确定性来推广该模型
在[28]中，作者重点关注了这个问题的几个实际考虑。首先，该算法考虑了种子集节点保持不活动状态的非零概率，即青年不参加训练。作者还通过提出基于友谊悖论的网络采样方法来解决网络构建步骤[86]。这个悖论表明，平均而言，随机节点的邻居比原始节点有更多的朋友。因此，在 M 个节点的采样预算下，他们首先随机采样 M/2 个节点，然后对每个节点随机采样一个邻居。这种方法增加了对中心（例如，有影响力的）节点进行采样的可能性。
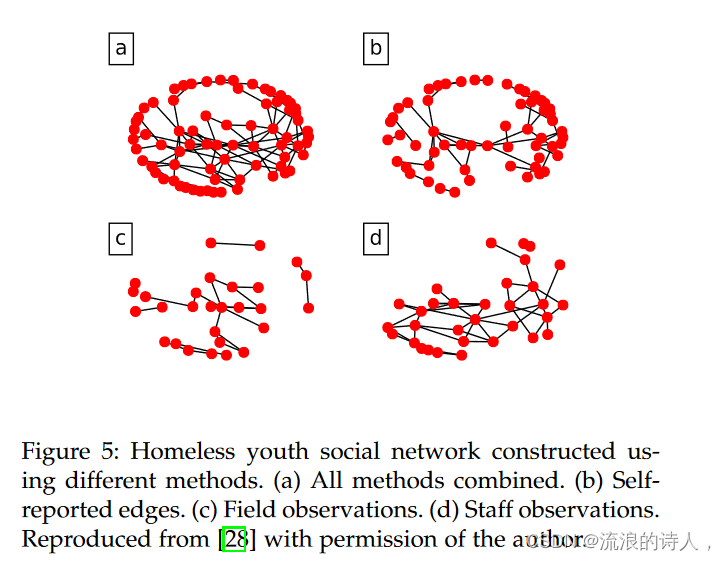
图5：使用不同方法构建的无家可归青年社交网络。 (a) 所有方法相结合。 (b) 自我报告的边缘。 (c) 实地观察。 (d) 工作人员的意见。经作者许可转载自[28]。
图5展示了使用不同方法构建的无家可归青年社交网络（经作者许可转载）。这四个网络凸显了为难以到达的人群构建网络的挑战，因为拓扑根据收集方法（自我报告、现场观察和无家可归者收容所工作人员观察）的不同而变化很大。接下来，作者假设影响传播概率未知，但进行建模以最大化真实传播与估计传播之间的最坏情况比率。最后，作者提出了一种贪心算法来选择最优种子节点，并证明它可以保证输出在最优因子 (e − 1)/(2e − 1) 范围内的解决方案。在现实世界的试点研究中，通过仅对 15% 的节点进行采样，所提出的方法与已知整个网络的情况相比，实现了可比的传播。
这些方法应用于[26]、[84]中的现实世界任务。考虑的一些关键问题是：激活的节点是否真的将其信息传递给其他节点？激活的节点是否提供有关社交网络的有意义的信息？这些算法能否比专家（社会工作者）更好地选择种子节点？为了回答这些问题，作者实现了[25]和[27]中的方法。他们还考虑了基于最大度数的基线 IM 算法。对于每种方法，作者都会招募研究参与者、构建网络、激活节点（通过训练）并进行后续行动以评估最终的影响力传播。 [25]和[27]中提出的方法比基于学位的方法产生了更大的影响力，同时也导致了参与者行为的改变，即增加了参与者艾滋病毒检测的数量。
最后，我们讨论IM在在线网络中的应用。环境。 [24]考虑一个“封闭”的社交网络，其中帖子仅与某些人而不是所有用户的联系共享。作为标准 IM 问题的一个细微变化，作者找到了用户应该与其分享信息以最大化传播的朋友。换句话说，目标是最大化影响力传播，其中用户只能与有限的边缘子集（邻居）共享信息。事实上，这对于社交网络来说可能是一种更现实的传播机制，因为某人不太可能付出同等的努力与每个朋友分享信息；相反，他/她可能会针对一些特定的人。作者将其应用于在线多人游戏，其中每个用户都被推荐与其互动的朋友，例如发送礼物、游戏邀请等。所提出的方法与随机选择朋友相比，点击率提高了 5%。
5 CONSIDERATIONS AND FUTURE DIRECTIONS
最后，我们分享了对与时间 IM 相关的挑战以及未来研究的一些重要领域的想法。\
Real-world implementations:
在第 4 节中，我们看到了研究人员在尝试针对现实问题实施 IM 算法时所面临的一系列挑战。我们列出了他/她在应用这些方法时必须考虑的一些问题：什么是信息传播机制？节点可以顺序更新，还是一开始就全部激活？种子节点一定会被激活吗？扩散过程持续多长时间？网络在什么时间尺度上发展？影响一个节点需要多长时间？网络动态变化很快吗？网络未来的拓扑结构需要预测吗？网络是通过在线设置还是通过标准快照进行更新的？真实的影响力分布是否已知？我们期待在实际应用中实现更多 IM。
Single seeding methods:
在第 2 节中，我们讨论了单种子时间 IM 问题的几种方法。然而，只有五篇论文，Aggarawal 等人。 [53]、Osawa 和 Murata [49] 以及 Erkol 等人。 [55]都提出了类似的解决方案。因此，这个问题还有很大的研究空间。最近，图神经网络（GNN）被应用于静态 IM 问题 [87]、[88]、[89]，并且也可能在时间设置中取得成功。
Ex ante vs. ex post:
第 2 节中提出的大多数方法都假设动态网络的整个拓扑是已知的，尽管这在许多情况下是不现实的。 [64]在事前 IM 方面取得了有希望的结果，但肯定需要做更多的工作。
Impact of time:
在具有扩散的动态网络中，结构演化和影响扩散之间存在高度复杂的关系。在类似于 Gayraud 等人的 IM 问题中必须仔细考虑这一点。 [62]和[63]。时间尺度、聚集、扩散时间和扩散机制的影响值得进一步研究。
Online setting:
与上一点相关的是在线环境中的IM，其中节点和边不断地来来去去。在现实世界的应用程序中，如何或何时聚合网络可能并不明显，因此考虑在线更新变得更加自然。然而，大多数方法要求将网络聚合成图快照。这种聚合本质上会丢失信息，例如链接何时出现/消失以及边缘的持久性。更多方法如 Ohsaka 等人。 [71]可以用来应对这一挑战。
Model mis-specification:
应用 IM 的一个相关挑战是选择扩散模型。对于疾病，SIR 模型是明智的，因为感染者只要被感染，就可以感染其他节点。另一方面，对于无家可归青少年的艾滋病毒认识而言，某人不太可能试图无限期地影响他/她的所有朋友。因此，选择合适的扩散模型至关重要。但如果模型指定错误，会对影响力传播产生什么影响呢？在[90]中，作者针对静态 IM 进行了研究，发现标准扩散模型严重低估了更现实模型的影响扩散。这可能只会在拓扑结构也发生变化的时间网络中复杂化。
Uncertainty estimates of seed nodes:
大多数时间 IM 算法输出最佳种子节点以实现最大影响力传播。但是还有其他种子组可以产生类似的传播吗？换句话说，目标函数是否“平坦”，即许多种子集产生可比的分布？一个有趣的研究途径是导出最佳种子集的不确定性度量。
Influence minimization:
与 IM 相关的一个问题是影响力最小化问题，其中种子节点被“接种”以阻止影响力在网络上的传播。这个问题出现在谣言传播和流行病学环境中[91]、[92]、[93]、[94]，并可能导致有趣的哲学问题。例如，在针对 COVID-19 的疫苗接种活动中，疫苗首先接种给最脆弱的人群，例如老年人。因此，根据脆弱性选择种子节点。然而，在影响最小化方案中，最活跃和/或最社交的人可能会首先接种疫苗，以最大程度地减少群体之间的传播。这些相反的目标导致在道德和政治上做出具有挑战性的决定。
这篇关于Influence maximization on temporal networks: a review的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
