eigen专题

使用 Eigen 库中的 Kronecker 积运算

前言在数值计算和线性代数的众多应用中，Kronecker 积（Kronecker Product）是一种常用的矩阵运算。Eigen 是一个高性能的 C++ 数值计算库，广泛用于科学计算和工程应用中。在 Eigen 库中，Kronecker 积运算属于不常用的扩展功能，因此被放置在 unsupported 模块中。本文将介绍如何在 Eigen 中使用 Kronecker 积，并解释为什么这个

Eigen::Tensor使用，定义高维矩阵

在实际项目中，需要存储大于等于三维的矩阵，而平常中我们使用Eigen::MatrixXd二维数据，这里我们使用Eigen::Tensor来定义 1.Using the Tensor module #include <unsupported/Eigen/CXX11/Tensor> 2.定义矩阵 2.一般矩阵官方文档 // 定义一个2x3x4大小的矩阵Eigen::Tensor<f

Ubuntu中PCL、Eigen、ROS、Ceres、VScode相关操作，安装，卸载，文件存储位置基础合集

Ubuntu中PCL相关操作查看PCL对应的版本号 apt-cache show libpcl-dev 卸载PCL相关命令 sudo apt-get remove libpcl-dev 如果想要完全卸载相关软件包及其配置文件，需要加上--purge参数： sudo apt-get --purge remove libpcl-dev Ubuntu中eigen相关操作 ubunt

CMake构建学习笔记9-Eigen库的构建

Eigen是一个高性能的C++线性代数库，广泛用于科学计算、机器学习、计算机视觉等领域。不过，Eigen有点特别，它是一个纯头文件实现的库；也就是说，任何一个程序要引入它，只要include它的头文件就可以了。这天然就规避了不同操作系统不同编译器造成的二进制兼容的问题，所有的实现都include源代码了，那还不是轻松跨平台？像Eigen这种风格的库就被称为Header Only库。这种库使用起

Eigen学习（二）

本文算是对官网手册的翻译吧，参考：http://eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html Matrix类在Eigen中，所有的矩阵和向量都是Matrix模板类的对象，向量只是特殊的矩阵而已，无论是行向量还是列向量。 Matrix类共有6个模板参数，主要使用的是前三个参数，剩余的都有默认值，前三个参数分别是 Matrix

LSSS算法实现，基于eigen和pbc密码库【一文搞懂LSSS，原理+代码】

文章目录一. LSSS简介1.1 概述1.2 线性秘密分享方案（LSSS）与 Shamir的秘密分享方案对比LSSS1.2.1 Shamir的秘密分享方案1.2.2 线性秘密分享方案（LSSS）1.2.3 主要区别二. 基于矩阵的LSSS加解密原理分析2.1 LSSS矩阵构造2.1.1 定义2.1.2 规则 12.1.3 规则 22.1.4 规则 32.1.5 形成线性共享矩阵M 2.

Eigen中 Row-Major 和 Column-Major 存储顺序的区别

Eigen中 Row-Major 和 Column-Major 存储顺序的区别 flyfish Eigen::RowMajor 是 Eigen 库中用于指定矩阵存储顺序的一种选项理解 Row-Major 和 Column-Major 存储顺序的区别，绘制一个单一的图来显示内存中的元素访问顺序,在图中用箭头表示访问顺序. import numpy as npimport matplotl

Eigen::Isometry3d变换矩阵的常用方法

文章目录 Eigen::Isometry3d变换矩阵的常用方法一、基本定义二、操作方法三、与四元数和平移向量的转换四、左乘与右乘 Eigen::Isometry3d变换矩阵的常用方法一、基本定义变换矩阵本质是一个4*4的矩阵 Eigen::Isometry3d T_imu_to_lidar = Eigen::Isometry3d::Identity() 二、操作方法

笔记100：使用 OSQP-Eigen 对 MPC 进行求解的方法与代码

1. 前言：我们在对系统进行建模的时候，为了减少计算量，一般都将系统简化为线性的，系统如果有约束，也是将约束简化为线性的；因此本篇博客只针对两种常见系统模型的 MPC 问题进行求解：线性系统 + 无约束线性系统 + 线性约束 a a a a 2. 线性系统 + 无约束的 MPC 问题求解目前已知：目标（代价）函数：矩阵，，均为正定矩阵；线性系统状态空

【eigen】——apt，conda安装方式

1. conda 只能使用官方的源进行安装 conda install -c conda-forge eigen Please update conda by running$ conda update -n base -c defaults conda## Package Plan ##environment location: /home/darknet/miniconda3/envs/t

Ubuntu18.04 重装/升级 eigen 教程

目录一、Eigen 1.1 ubuntu 查看 eigen 版本 1.2 卸载老版本 eigen 二、安装 eigen 3.4.0 2.1 配置安装 2.2 查看版本一、Eigen 1.1 ubuntu 查看 eigen 版本 $ dpkg -l | grep eigen 1.2 卸载老版本 eigen sudo updatedblocate eigen3

使用Eigen将经纬度、高程、偏北角转成变换矩阵

目录 1、前言 2、示例 3、代码解析 4、垂直于给定点的切平面变换 5、代码解析 1、前言在地球表面进行刚体变换时候，要将具有经纬度、高程和偏北角的坐标信息转换为变换矩阵表达，首先需要了解坐标系之间的转换关系。通常，我们会将经纬度坐标转换为地心坐标系（ECEF坐标系），然后再根据高程和偏北角进行变换。 2、示例 #include <iostream>#i

C++之Eigen库基本使用（下）

1、常见变换 Eigen::Matrix3d //旋转矩阵（3*3）Eigen::AngleAxisd //旋转向量（3*1）Eigen::Vector3d //欧拉角（3*1）Eigen::Quaterniond //四元数（4*1）Eigen::Isometry3d //欧式变换矩阵（4*4）Eigen::Affine3d //放射

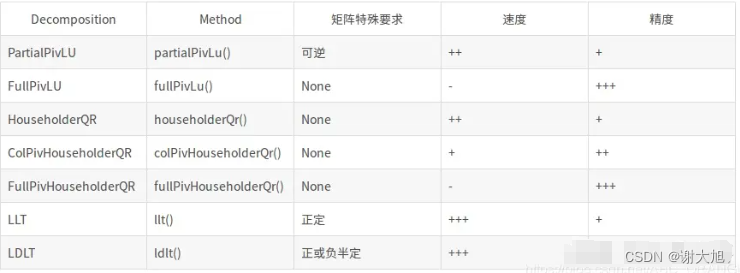
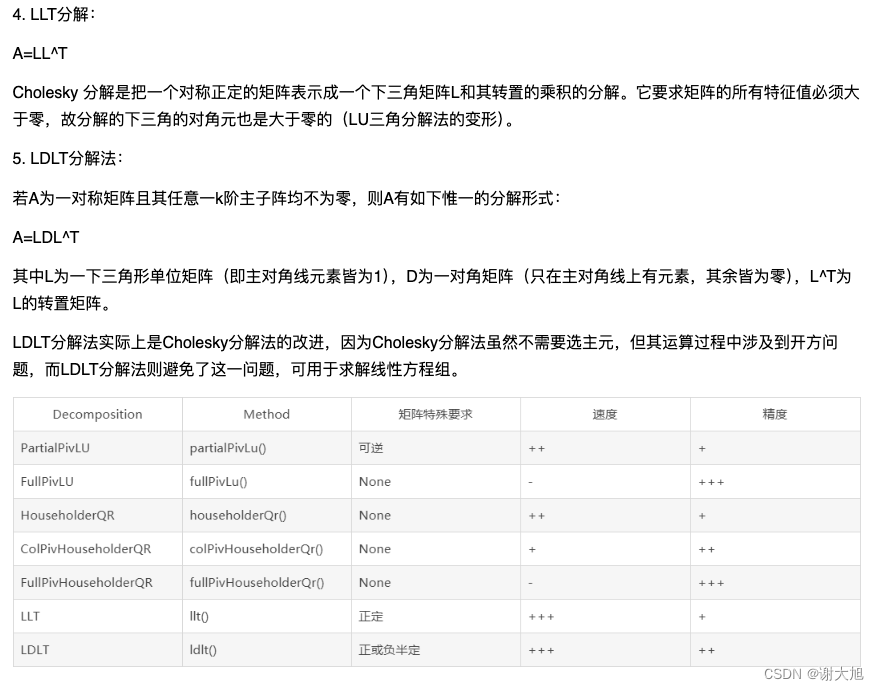
Eigen求解线性方程组

1、线性方程组的应用线性方程组可以用来解决各种涉及线性关系的问题。以下是一些通常可以用线性方程组来解决的问题：在实际工程和科学计算中，求解多项式方程的根有着广泛的应用。在控制系统的设计中，我们经常需要求解特征方程的根来分析系统的稳定性; 在图像处理和模式识别中，多项式方程的根可以用来寻找图像的特征点; 在金融工程和风险管理中，多项式方程的根可以用来对数据进行拟合和预测。工程问

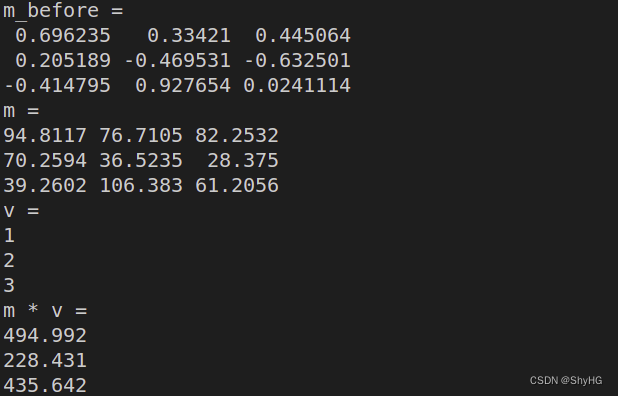
eigen在c++的基本使用，矩阵运算，几何运算

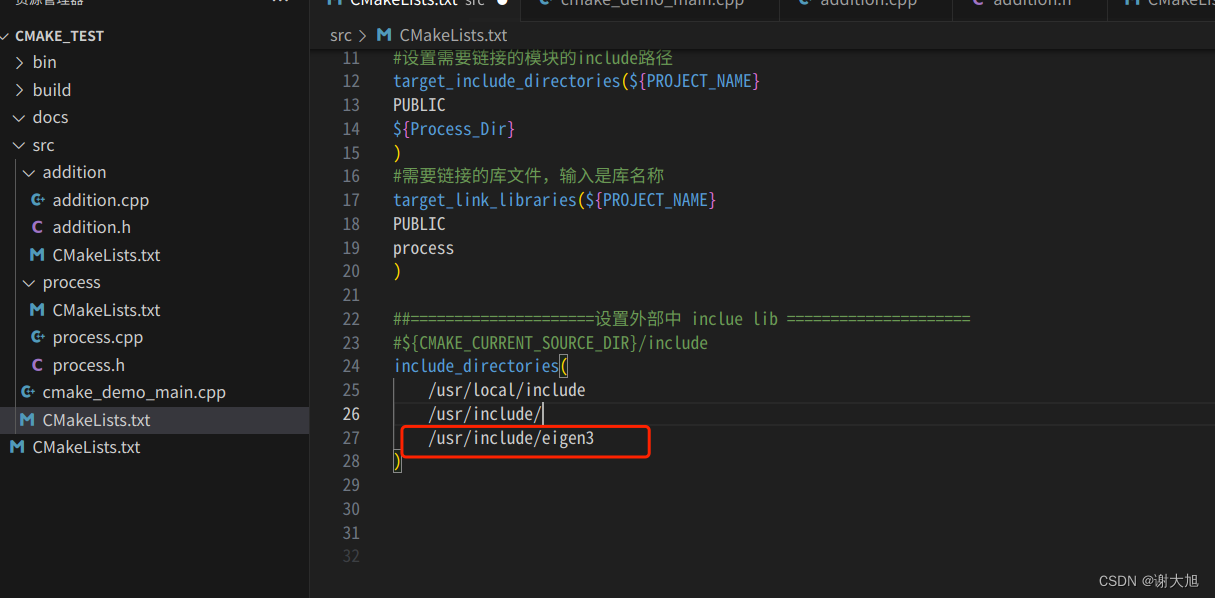
矩阵运算 CMakeLists.txt文件 cmake_minimum_required(VERSION 3.2)project(useEigen)set(CMAKE_BUILD_TYPE "Release")set(CMAKE_CXX_FLAGS "-O3")include_directories("/usr/include/eigen3")add_executable(eigenMa

pcl中Eigen::Affine3f变换点云异常

问题来源在使用pcl::transformPointCloudWithNormals变换点云的时候出现异常，即变换后的点云非原始点云的形状；为什么？主要是在创建Eigen::Affine3f时没有对旋转矩阵进行归一化，导致变换后的点云出现异常；解决方案：对旋转矩形进行归一化操作；即在使用Eigen::Affine3f需要时刻想到归一化问题；创建Eigen::Affin

C++之Eigen使用（使用cmake）

1、eigen安装安装命令如下： sudo apt-get updatesudo apt-get install libeigen3-dev 默认安装路径为： /usr/include/eigen3 2、使用cmake 添加eigen头文件，由于eigen只有头文件，因此只要添加头文件即可。 3、其他 3.1 cmake内置变量 C

Eigen库从入门到放弃(2. Getting Started)

Eigen的头文件定义了多种类型，但是对于简单的来说，使用MatrixXd就足够了，MatrixXd表示任意尺寸的矩阵，但是要注意数据类型是double的。Eigen/Dense的头文件定义了所有MatrixXd和相关类型的成员函数。所有头文件中定义的函数都是在Eigen这个命名空间下的。我们再次分析一下上面的代码： MatrixXd m(2,2); // 定义两行两列，前面是行数，后面是列

C++版NumPy-Eigen库快速入门

Eigen库的使用零、前言一、Eigen矩阵类1、矩阵类模板参数2、向量3、特值动态4、矩阵和向量的初始化5、矩阵和向量的存取6、逗号初始化7、调整大小二、矩阵和向量算法1、加减2、标量乘法和除法3、转置、共轭和伴随4、矩阵矩阵和矩阵向量乘法5、点积和叉积6、基本算术归约运算7、操作的有效性三、数组类和按系数运算1、数组类2、访问数组内的值3、加减4、数组乘法5、其他系数运算6、在数组和

《OpenCV编译》十三、编译Eigen

1、下载Eigen；下载地址：http://eigen.tuxfamily.org/index.php?title=Main_Page 2、打开CMake开始编译，选择源码位置和build位置 3、配置编译环境 4、勾选项如下： 5、生成解决方案并打开项目 6、VS2017中，使用批生成，只选择Install即可 7、生成成功

C++之eigen库学习

Eigen是一个高性能的C++模板库，专门用于线性代数、矩阵和向量运算。该库提供了一系列的类和函数，使开发者能够轻松进行各种数学计算，如矩阵乘法、矩阵分解（如QR分解、奇异值分解等）、特征值计算、求解线性方程组等。以下是Eigen库的一些主要特点：模板化设计：Eigen完全基于C++模板编写，这使得它能够提供高度的代码灵活性和优化能力。通过模板化设计，Eigen能够自动生成适合特定数据类型

Eigen教程:C++线性代数库详解

Eigen是一个高效、优雅的C++模板库,用于线性代数、矩阵和向量运算、数值分析及其相关算法。它提供了类似Matlab的语法和接口,使得编写代码变得简洁明了。Eigen经过精心设计,充分发挥了C++语言的优势,在运行效率、内存管理等方面表现出色。本文将详细介绍Eigen库的使用方法,并提供丰富的代码示例,帮助读者快速入门并掌握这一强大工具。一、Eigen简介 Eigen是一个开源的C++

小技巧系列——Ubuntu下查看Eigen版本的一种方法（一）

小技巧系列——Ubuntu下查看Eigen版本的一种方法（一）说明命令说明如何在Ubuntu下查看Eigen版本命令 pkg-config --modversion eigen3

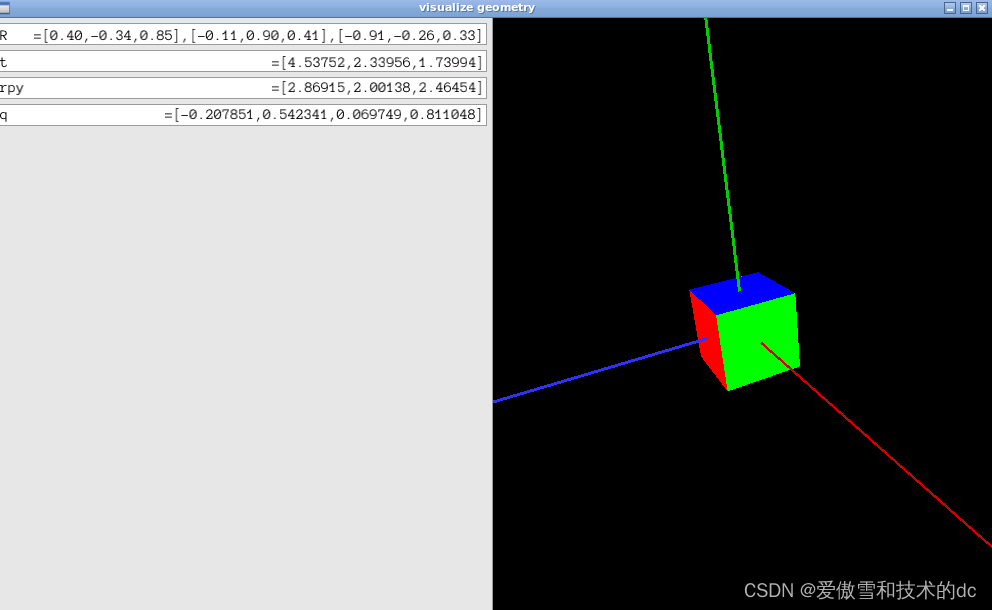
slam三维空间刚体运动及Eigen库的使用

1.理论部分 1.旋转矩阵旋转矩阵有一些特别的性质。事实上，它是一个行列式为 1 的正交矩阵。反之，行列式为 1 的正交矩阵也是一个旋转矩阵。所以，我们可以把旋转矩阵的集合定义如下：由于旋转矩阵为正交阵，显然 RT 刻画了一个相反的旋转。我们把一个三维向量的末尾添加 1，变成了四维向量，称为齐次坐标。齐次坐标。它是射影几何里的概念。通过添加最后一维，我们用四个实数

ubuntu安装使用eigen（vscode）

1、eigen安装安装命令如下： sudo apt-get updatesudo apt-get install libeigen3-dev 默认安装路径为： /usr/include/eigen3 安装版本查询命令： pkg-config --modversion eigen3 2、CMakeLists.txt cmake_

应用Eigen 的项目

文章目录扩展，数值计算绑定科学机器人与工程计算机图形学、几何学、可视化移动应用KDE（Eigen的起源）扩展，数值计算 Google 的 TensorFlow 是一个用于机器智能的开源软件库谷歌的Ceres求解器是一个可移植的C++库，允许建模和求解大型复杂的非线性最小二乘问题。 Manifold ToolKit MTK 提供了简单的机制，使任意算法能够在流形上运行。它还提