本文主要是介绍slam三维空间刚体运动及Eigen库的使用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.理论部分
1.旋转矩阵

旋转矩阵有一些特别的性质。事实上,它是一个行列式为 1 的正交矩阵。反之,行
列式为 1 的正交矩阵也是一个旋转矩阵。所以,我们可以把旋转矩阵的集合定义如下:
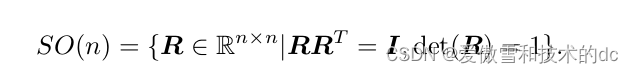
由于旋转矩阵为正交阵,显然 RT 刻画了一个相反的旋转。
我们把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。
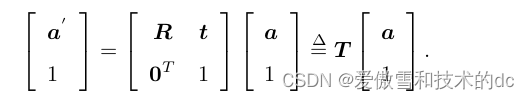
齐次坐标。它是射影几何里的概念。通过添加最后一维,我们用四个实数描述了一个三维向量,这显然多了一个自由度,但允许我们把变换写成线性的形式。
这时,忽略掉最后一项,这个点的坐标和欧氏空间就是一样的。依靠齐次坐标和变换矩阵,两次变换的累加就可以有很好的形式:
关于变换矩阵 T ,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):

最后,为了保持符号的简洁,在不引起歧义的情况下,我们以后不区别齐次坐标与普
通的坐标的符号,默认我们使用的是符合运算法则的那一种。例如,当我们写 T a 时,使
用的是齐次坐标(不然没法计算)。而写 Ra 时,使用的是非齐次坐标。如果写在一个等
式中,我们就假设齐次坐标到普通坐标的转换,是已经做好了的——因为齐次坐标和非齐
次坐标之间的转换事实上非常容易。
2.旋转向量
有了旋转矩阵来描述旋转,有了变换矩阵描述一个六自由度的三维刚体运动。但是,矩阵表示方式至少有以下几个缺点:
1. SO(3) 的旋转矩阵有九个量,但一次旋转只有三个自由度。因此这种表达方式是冗
余的。同理,变换矩阵用十六个量表达了六自由度的变换。
2. 旋转矩阵自身带有约束:它必须是个正交矩阵,且行列式为 1。变换矩阵也是如此。当
我们想要估计或优化一个旋转矩阵/变换矩阵时,这些约束会使得求解变得更困难。
任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(或轴角,Axis-Angle)。
这种表示法只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。
事实上,旋转向量就是李代数
假设有一个旋转轴为 n,角度为 θ 的旋转,显然,它对应的旋转向
量为 θn。由旋转向量到旋转矩阵的过程由罗德里格斯公式(Rodrigues’s Formula )
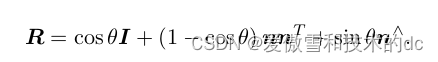
我们也可以计算从一个旋转矩阵到旋转向量的转换。对于转角 θ,有
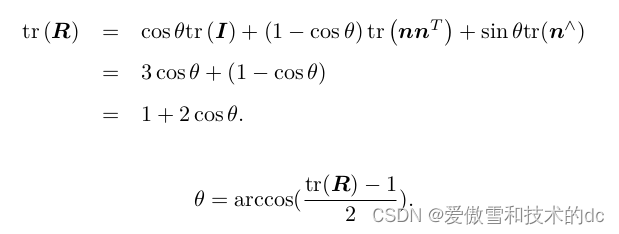
关于转轴 n,由于旋转轴上的向量在旋转后不发生改变,说明

因此,转轴 n 是矩阵 R 特征值 1 对应的特征向量。求解此方程,再归一化,就得到
了旋转轴。
3.欧拉角
而欧拉角则提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角
ZY X 转角相当于把任意旋转分解成
以下三个轴上的转角:
1. 绕物体的 Z 轴旋转,得到偏航角 yaw;
2. 绕旋转之后的 Y 轴旋转,得到俯仰角 pitch;
3. 绕旋转之后的 X 轴旋转,得到滚转角 roll。
此时,我们可以使用 [r, p, y]T 这样一个三维的向量描述任意旋转。
欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock¬ ):在俯仰角为
±90◦ 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次
旋转变成了两次旋转)。这被称为奇异性。
由于这种原理,欧拉角不适于插值和迭代,往往只用于人机交互中。我们也很少在 SLAM程序中直接使用欧拉角表达姿态,同样不会在滤波或优化中使用欧拉角表达旋转(因为它
具有奇异性)。不过,若你想验证自己算法是否有错时,转换成欧拉角能够快速辨认结果的
正确与否
4.四元数
旋转矩阵用九个量描述三自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但
具有奇异性。事实上,我们找不到不带奇异性的三维向量描述方式。三维旋转是一个三维流形,想要无奇异性地表达它,用三个量是不够的。
在表达三维空间旋转时,也有一种类似于复数的代数:四元数(Quaternion)。四元数
是 Hamilton 找到的一种扩展的复数. 它既是紧凑的,也没有奇异性。
一个四元数 q 拥有一个实部和三个虚部


从旋转向量到四元数

四元数到旋转矩阵的转换方式

最后,无论是四元数、旋转矩阵还是轴角,它们都可以用来描述同一个旋转。我们应
该在实际中选择对我们最为方便的形式
5.相似、仿射、射影变换
1. 相似变换
相似变换比欧氏变换多了一个自由度,它允许物体进行均匀的缩放,其矩阵表示为:
 注意到旋转部分多了一个缩放因子 s,表示我们在对向量旋转之后,可以在 x, y, z 三个坐标上进行均匀的缩放。由于含有缩放,相似变换不再保持图形的面积不变。
注意到旋转部分多了一个缩放因子 s,表示我们在对向量旋转之后,可以在 x, y, z 三个坐标上进行均匀的缩放。由于含有缩放,相似变换不再保持图形的面积不变。
2. 仿射变换

3. 射影变换
 从真实世界到相机照片的变换是一个射影变换。
从真实世界到相机照片的变换是一个射影变换。
2.Eigen线性代数模块
Eigen¬ 是一个 C++ 开源线性代数库。它提供了快速的有关矩阵的线性代数运算,还
包括解方程等功能。许多上层的软件库也使用 Eigen 进行矩阵运算,包括 g2o、Sophus 等。
比于其他库,Eigen 特殊之处在于,它是一个纯用头文件搭建起来的
库(这非常神奇!)。这意味着你只能找到它的头文件,而没有.so 或.a 那样的二进制文件。
我们在使用时,只需引入 Eigen 的头文件即可,不需要链接它的库文件(因为它没有库文
件)。
// 包含标准输入输出流库,用于控制台输入输出
#include <iostream>
// 使用std命名空间,避免在每次使用标准库时都需要前缀std::
using namespace std;// 包含C++时间库,用于计算代码运行时间
#include <ctime>
// 引入Eigen库的核心部分,定义了矩阵、向量等基本数据结构
#include <Eigen/Core>
// 引入Eigen库用于进行稠密矩阵的代数运算(如求逆、求特征值等)
#include <Eigen/Dense>// 使用Eigen命名空间,简化类型名称
using namespace Eigen;// 定义一个宏,用作矩阵大小的常量,这里设置为50
#define MATRIX_SIZE 50int main(int argc, char **argv) {// Eigen库中所有向量和矩阵都是Eigen::Matrix的实例,这是一个模板类。// 它的前三个参数为:数据类型,行数,列数// 声明一个2x3的float矩阵Matrix<float, 2, 3> matrix_23;// Eigen通过typedef提供了许多内置类型,但底层仍是Eigen::Matrix// 例如,Vector3d实际上是Eigen::Matrix<double, 3, 1>,即三维向量Vector3d v_3d;// 同样的,这是另一个三维向量Matrix<float, 3, 1> vd_3d;// Matrix3d实际上是Eigen::Matrix<double, 3, 3>Matrix3d matrix_33 = Matrix3d::Zero(); // 初始化为零// 对于不确定大小的矩阵,可以使用动态大小的矩阵Matrix<double, Dynamic, Dynamic> matrix_dynamic;// 更简单的动态矩阵声明方式MatrixXd matrix_x;// 接下来是对Eigen矩阵的一些操作// 输入数据(初始化)matrix_23 << 1, 2, 3, 4, 5, 6;// 输出矩阵内容cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;// 使用()访问矩阵中的元素cout << "print matrix 2x3: " << endl;for (int i = 0; i < 2; i++) {for (int j = 0; j < 3; j++)cout << matrix_23(i, j) << "\t";cout << endl;}// 矩阵和向量相乘(实际上是矩阵和矩阵)v_3d << 3, 2, 1;vd_3d << 4, 5, 6;// 在Eigen中不能混合不同类型的矩阵,需要类型转换Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;cout << "[1,2,3;4,5,6]*[3,2,1]=" << result.transpose() << endl;Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;cout << "[1,2,3;4,5,6]*[4,5,6]: " << result2.transpose() << endl;// 对矩阵的一些基本运算matrix_33 << 1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0;cout << "matrix 3x3: \n" << matrix_33 << endl;cout << "transpose: \n" << matrix_33.transpose() << endl; // 矩阵转置cout << "sum: " << matrix_33.sum() << endl; // 矩阵所有元素的和cout << "trace: " << matrix_33.trace() << endl; // 矩阵的迹(对角线元素之和)cout << "times 10: \n" << 10 * matrix_33 << endl; // 矩阵的每个元素乘以10cout << "inverse: \n" << matrix_33.inverse() << endl; // 矩阵的逆cout << "det: " << matrix_33.determinant() << endl; // 矩阵的行列式值// 求解特征值和特征向量,这里使用SelfAdjointEigenSolver求解自伴矩阵的特征问题// 由于matrix_33.transpose() * matrix_33总是自伴的,因此可以这样做SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;// 解线性方程组// 我们要解的方程是 matrix_NN * x = v_Nd// 其中 matrix_NN 是一个随机的正定矩阵,v_Nd 是一个随机向量// MATRIX_SIZE是之前定义的50,表示我们用50x50的矩阵和50维向量Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);matrix_NN = matrix_NN * matrix_NN.transpose(); // 乘以其转置以确保是半正定Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);// 记录当前时间clock_t time_stt = clock();// 直接使用矩阵逆求解Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;cout << "time of normal inverse is " << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;cout << "x = " << x.transpose() << endl;// 使用QR分解求解,通常比直接求逆快很多time_stt = clock();x = matrix_NN.colPivHouseholderQr().solve(v_Nd);cout << "time of QR decomposition is " << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;cout << "x = " << x.transpose() << endl;// 对于正定矩阵,还可以使用cholesky分解来求解time_stt = clock();x = matrix_NN.ldlt().solve(v_Nd);cout << "time of ldlt decomposition is " << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;cout << "x = " << x.transpose() << endl;return 0;
}
out
matrix 2x3 from 1 to 6:
1 2 3
4 5 6
print matrix 2x3:
1 2 3
4 5 6
[1,2,3;4,5,6]*[3,2,1]=10 28
[1,2,3;4,5,6]*[4,5,6]: 32 77
random matrix:
1 2 3
4 5 6
7 8 9
transpose:
1 4 7
2 5 8
3 6 9
sum: 45
trace: 15
times 10:
10 20 30
40 50 60
70 80 90
inverse:
-inf inf -infinf -inf inf
-inf inf -inf
det: 0
Eigen values =
9.30184e-161.14141283.859
Eigen vectors = -0.408248 -0.776691 0.4796710.816497 -0.0756865 0.572368-0.408248 0.625318 0.665064
time of normal inverse is 0.079ms
x = 2.91155 10.6997 3.43027 -2.6258 -1.14637 1.55867 1.03946 3.68188 -13.0695 1.87163 2.80044 9.72767 9.88619 -6.15914 2.10578 0.450982 -3.58146 -3.01118 8.34067 10.5629 -0.681178 4.72464 -6.14278 -0.191873 3.41807 -3.36318 2.64461 -8.38439 0.620947 -5.11558 -7.43408 -2.18593 -3.23169 0.194099 -2.69517 7.2354 -4.10885 -3.74595 -4.52556 -11.9484 8.27016 7.33514 0.384987 3.41304 -1.809 9.19733 -0.121441 -8.20668 1.72084 4.577
time of Qr decomposition is 0.046ms
x = 2.91155 10.6997 3.43027 -2.6258 -1.14637 1.55867 1.03946 3.68188 -13.0695 1.87163 2.80044 9.72767 9.88619 -6.15914 2.10578 0.450982 -3.58146 -3.01118 8.34067 10.5629 -0.681178 4.72464 -6.14278 -0.191873 3.41807 -3.36318 2.64461 -8.38439 0.620947 -5.11558 -7.43408 -2.18593 -3.23169 0.194099 -2.69517 7.2354 -4.10885 -3.74595 -4.52556 -11.9484 8.27016 7.33514 0.384987 3.41304 -1.809 9.19733 -0.121441 -8.20668 1.72084 4.577
time of ldlt decomposition is 0.021ms
x = 2.91155 10.6997 3.43027 -2.6258 -1.14637 1.55867 1.03946 3.68188 -13.0695 1.87163 2.80044 9.72767 9.88619 -6.15914 2.10578 0.450982 -3.58146 -3.01118 8.34067 10.5629 -0.681178 4.72464 -6.14278 -0.191873 3.41807 -3.36318 2.64461 -8.38439 0.620947 -5.11558 -7.43408 -2.18593 -3.23169 0.194099 -2.69517 7.2354 -4.10885 -3.74595 -4.52556 -11.9484 8.27016 7.33514 0.384987 3.41304 -1.809 9.19733 -0.121441 -8.20668 1.72084 4.577
矩阵论前置知识
1.特征值和特征向量

2.自伴矩阵
自伴矩阵:在数学中,特别是线性代数中,自伴矩阵(也称为Hermite矩阵或对称矩阵,在实数域上)是指其转置矩阵和共轭矩阵等于其本身的矩阵。在这个代码示例中,通过matrix_33.transpose() * matrix_33生成一个自伴矩阵,因为任何矩阵与其转置的乘积都是自伴的。

3.正定矩阵

正定矩阵应用
优化问题
在优化问题中,目标函数的Hessian矩阵(二次导数矩阵)如果在某点正定,那么该点是一个局部最小点。这一性质被广泛用于确定优化算法是否达到了局部最小值,尤其是在梯度下降法和牛顿法等方法中。
机器学习
在机器学习中,核函数(Kernel)矩阵或称为克拉默矩阵(Gram matrix)在支持向量机(SVM)等算法中扮演关键角色,其必须是半正定的,以确保优化问题的凸性,从而保证找到全局最优解。
信号处理
在信号处理和统计学中,协方差矩阵描述了各个变量间的协方差,是一个半正定矩阵。协方差矩阵的性质被用来分析数据的分布和变量之间的关系。
控制理论
在控制理论中,系统的稳定性可以通过Lyapunov函数来分析,其二次形式的正定性是判断系统稳定性的一个重要工具。
量子力学
在量子力学中,密度矩阵描述了量子系统的状态,它是半正定的。这一性质用于确保概率解释的一致性和物理可行性。
4.正交矩阵

正交矩阵性质
- 行列向量的正交性:正交矩阵的行和列都是标准正交基,即它们的内积为0(对不同行或列),自身的内积为1。
- 保持内积和长度:正交变换保持向量的内积和长度不变,因此也保持了向量间的角度。
- 行列式的值:正交矩阵的行列式值为+1+1或−1−1,表示经过正交变换后,空间的体积(或面积)保持不变,仅方向可能发生改变。
正交矩阵用途
-
几何变换:在几何中,正交矩阵用于表示各种保持长度和角度不变的变换,如旋转、反射。这在图形处理、计算机视觉等领域尤其重要。
-
数值稳定的算法:在数值线性代数中,正交矩阵因其数值稳定性特别有用。例如,QR分解就是将矩阵分解为一个正交矩阵和一个上三角矩阵的乘积,广泛应用于求解线性方程组、计算特征值等。
-
信号处理:在信号处理领域,正交矩阵用于设计正交滤波器和进行正交变换(如离散傅立叶变换、离散余弦变换),以实现有效的信号分析和数据压缩。
-
通信理论:在通信理论中,正交码被用来设计抗干扰的通信系统,确保信号传输的准确性。
-
量子计算:在量子计算中,量子位的操作可以通过酉矩阵(正交矩阵的复数推广)来表示,这对于设计和理解量子算法至关重要。
求解线性方程组
1.使用矩阵逆求解
这种求解线性方程组的方法简单直接,但在实际应用中,尤其是对于大规模矩阵,直接计算矩阵的逆可能不是最高效或最稳定的方法。原因包括:
- 计算复杂度:求一个矩阵的逆的复杂度较高,尤其是对于大矩阵,可能会导致计算成本过大。
- 数值稳定性:直接求逆可能会引入数值不稳定性,尤其是当矩阵条件数(condition number)较大时。
在实践中,更倾向于使用如LU分解、QR分解或者奇异值分解(SVD)等数值稳定的算法来求解线性方程组。这些方法不仅能提高计算效率,还能增加数值计算的稳定性。
- 这种方法直接应用了线性代数中的公式
x = A^(-1) * b,其中A是系数矩阵,b是结果向量,x是未知向量。
2.QR分解
QR分解是将矩阵分解为一个正交矩阵(Q)和一个上三角矩阵(R)的乘积。对于任何矩阵A,都可以分解为A = QR,其中Q是一个具有正交列的矩阵,而R是一个上三角矩阵。
当用于求解线性方程组Ax = b时,通过将A分解为QR,原方程变为QRx = b。由于Q是正交的,即Q^TQ = I(其中I是单位矩阵),我们可以两边同时左乘Q^T得到R x = Q^T b。由于R是上三角矩阵,这个新的方程组可以通过回代法(back substitution)高效解决。
回代法(Back Substitution)是一种用于求解上三角线性方程组的算法。在上三角矩阵中,所有的未知数都排列在方程的对角线及其右侧,这使得可以从最后一个方程开始依次解出每个未知数。

3.Cholesky(LDLT)分解

 因此,在知道矩阵是对称正定的情况下,优先考虑使用Cholesky分解,因为它更高效且数值稳定。在矩阵类型未知或不满足Cholesky分解条件时,使用LU分解。
因此,在知道矩阵是对称正定的情况下,优先考虑使用Cholesky分解,因为它更高效且数值稳定。在矩阵类型未知或不满足Cholesky分解条件时,使用LU分解。
3.Eigen几何模块
#include <iostream> // 引入标准输入输出流库
#include <cmath> // 引入数学函数库using namespace std; // 使用标准命名空间#include <Eigen/Core> // 引入Eigen的核心部分
#include <Eigen/Geometry> // 引入Eigen的几何模块using namespace Eigen; // 使用Eigen命名空间int main(int argc, char **argv) {Matrix3d rotation_matrix = Matrix3d::Identity(); // 初始化一个3x3的单位旋转矩阵// 定义旋转向量,表示沿Z轴旋转45度
//AngleAxisd是Eigen中用于表示旋转的一种方式,其构造函数接收两个参数:旋转角度和旋转轴
//(在这个例子中是Z轴,即向量(0, 0, 1))。AngleAxisd rotation_vector(M_PI / 4, Vector3d(0, 0, 1));// 输出旋转矩阵cout.precision(3); // 设置输出精度cout << "rotation matrix =\n" << rotation_vector.matrix() << endl; // 转换旋转向量为旋转矩阵并输出// 将AngleAxis对象转换为旋转矩阵rotation_matrix = rotation_vector.toRotationMatrix();// 使用旋转向量对向量(1,0,0)进行旋转Vector3d v(1, 0, 0);Vector3d v_rotated = rotation_vector * v;cout << "(1,0,0) after rotation (by angle axis) = " << v_rotated.transpose() << endl;// 使用旋转矩阵对向量进行旋转v_rotated = rotation_matrix * v;cout << "(1,0,0) after rotation (by matrix) = " << v_rotated.transpose() << endl;// 将旋转矩阵转换为欧拉角Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // 按照Z, Y, X顺序转换为欧拉角cout << "yaw pitch roll = " << euler_angles.transpose() << endl;// 定义一个Isometry3d对象T,用于表示3D空间中的旋转和平移Isometry3d T = Isometry3d::Identity();T.rotate(rotation_vector); // 应用旋转T.pretranslate(Vector3d(1, 3, 4)); // 应用平移cout << "Transform matrix = \n" << T.matrix() << endl; // 输出变换矩阵// 使用变换矩阵T对向量v进行变换Vector3d v_transformed = T * v;cout << "v transformed = " << v_transformed.transpose() << endl;// 定义一个四元数q,从旋转向量初始化Quaterniond q = Quaterniond(rotation_vector);cout << "quaternion from rotation vector = " << q.coeffs().transpose() << endl;// 也可以从旋转矩阵初始化四元数qq = Quaterniond(rotation_matrix);cout << "quaternion from rotation matrix = " << q.coeffs().transpose() << endl;// 使用四元数q对向量v进行旋转v_rotated = q * v; // 注意,这里使用的是四元数的旋转操作cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;// 计算等价的四元数乘法,应与上面的旋转结果相同cout << "should be equal to " << (q * Quaterniond(0, 1, 0, 0) * q.inverse()).coeffs().transpose() << endl;return 0;
}
out
rotation matrix =0.707 -0.707 00.707 0.707 00 0 1
(1,0,0) after rotation (by angle axis) = 0.707 0.707 0
(1,0,0) after rotation (by matrix) = 0.707 0.707 0
yaw pitch roll = 0.785 -0 0
Transform matrix = 0.707 -0.707 0 10.707 0.707 0 30 0 1 40 0 0 1
v tranformed = 1.71 3.71 4
quaternion from rotation vector = 0 0 0.383 0.924
quaternion from rotation matrix = 0 0 0.383 0.924
(1,0,0) after rotation = 0.707 0.707 0
should be equal to 0.707 0.707 0 0
Eigen 中对各种形式的表达方式总结如下。请注意每种类型都有单精度和双精度两种
数据类型,而且和之前一样,不能由编译器自动转换。下面以双精度为例,你可以把最后
的 d 改成 f,即得到单精度的数据结构。
• 旋转矩阵(3 × 3)
:Eigen::Matrix3d。
• 旋转向量(3 × 1)
:Eigen::AngleAxisd。
• 欧拉角(3 × 1)
:Eigen::Vector3d。
• 四元数(4 × 1)
:Eigen::Quaterniond。
• 欧氏变换矩阵(4 × 4)
:Eigen::Isometry3d。
• 仿射变换(4 × 4)
:Eigen::Affine3d。
• 射影变换(4 × 4)
:Eigen::Projective3d。
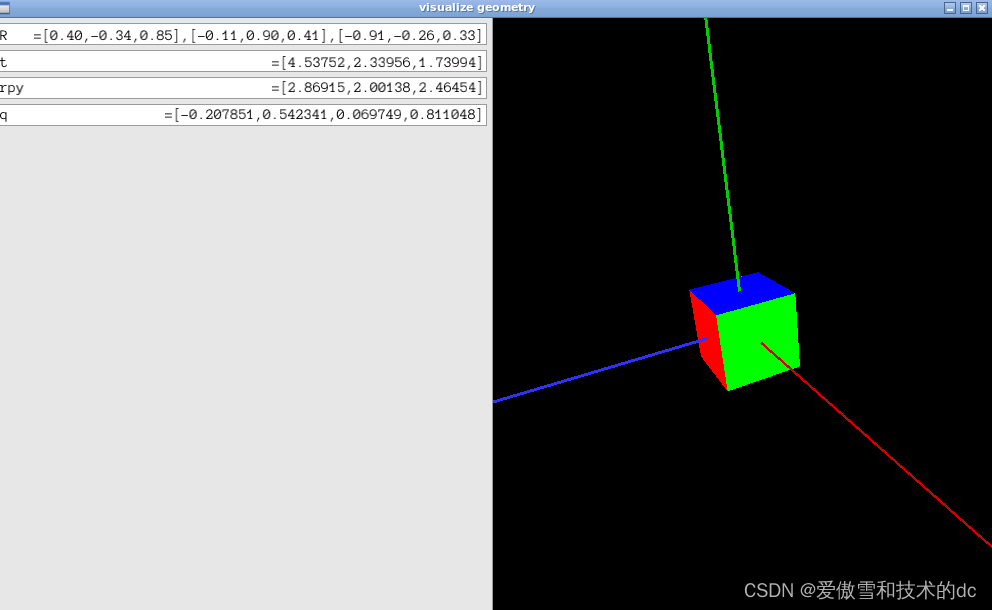
4.Pangolin库和Eigen库可视化
Pangolin是一个轻量级的3D视觉化库,常用于计算机视觉和机器人项目中。
#include <iostream> // 引入标准输入输出流库
#include <iomanip> // 引入输入输出流格式控制库using namespace std; // 使用标准命名空间#include <Eigen/Core> // 引入Eigen的核心部分
#include <Eigen/Geometry> // 引入Eigen的几何模块,用于处理3D空间的旋转和变换using namespace Eigen; // 使用Eigen命名空间#include <pangolin/pangolin.h> // 引入Pangolin库// 定义旋转矩阵结构体,封装了Eigen的Matrix3d作为成员变量
struct RotationMatrix {Matrix3d matrix = Matrix3d::Identity(); // 默认初始化为单位矩阵
};// 重载输出流运算符,用于输出旋转矩阵
ostream &operator<<(ostream &out, const RotationMatrix &r) {out.setf(ios::fixed); // 设置输出格式为固定点表示法Matrix3d matrix = r.matrix; // 获取旋转矩阵// 格式化输出矩阵元素out << '=';out << "[" << setprecision(2) << matrix(0, 0) << "," << matrix(0, 1) << "," << matrix(0, 2) << "],"<< "[" << matrix(1, 0) << "," << matrix(1, 1) << "," << matrix(1, 2) << "],"<< "[" << matrix(2, 0) << "," << matrix(2, 1) << "," << matrix(2, 2) << "]";return out;
}// 由于没有定义输入格式,该重载的输入流运算符仅返回输入流对象
istream &operator>>(istream &in, RotationMatrix &r) {return in;
}// 定义平移向量结构体,封装了Eigen的Vector3d作为成员变量
struct TranslationVector {Vector3d trans = Vector3d(0, 0, 0); // 默认初始化为零向量
};// 重载输出流运算符,用于输出平移向量
ostream &operator<<(ostream &out, const TranslationVector &t) {// 格式化输出向量元素out << "=[" << t.trans(0) << ',' << t.trans(1) << ',' << t.trans(2) << "]";return out;
}// 同样,由于没有定义输入格式,该重载的输入流运算符仅返回输入流对象
istream &operator>>(istream &in, TranslationVector &t) {return in;
}// 定义四元数绘制结构体,封装了Eigen的Quaterniond作为成员变量
struct QuaternionDraw {Quaterniond q;
};// 重载输出流运算符,用于输出四元数
ostream &operator<<(ostream &out, const QuaternionDraw quat) {auto c = quat.q.coeffs(); // 获取四元数的系数// 格式化输出四元数的系数,注意四元数的系数顺序为(x, y, z, w)out << "=[" << c[0] << "," << c[1] << "," << c[2] << "," << c[3] << "]";return out;
}// 同样,由于没有定义输入格式,该重载的输入流运算符仅返回输入流对象
istream &operator>>(istream &in, const QuaternionDraw quat) {return in;
}int main(int argc, char **argv) {// 创建一个名为"visualize geometry"的Pangolin窗口,尺寸为1000x600pangolin::CreateWindowAndBind("visualize geometry", 1000, 600);
out
这篇关于slam三维空间刚体运动及Eigen库的使用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






