三维空间专题
基于粒子群优化算法的六自由度机械臂三维空间避障规划
摘要:本研究旨在解决机械臂在复杂环境中避障路径规划的问题。本文提出了一种利用粒子群优化算法(PSO)进行机械臂避障规划的方法,通过建立机械臂的运动模型,将避障问题转化为优化问题。PSO算法通过模拟群体中个体的社会行为和个体行为来寻找到最佳路径,确保机械臂在避开障碍物的同时,能够高效地到达目标位置。研究表明,基于PSO算法的避障规划在收敛速度和路径优化上具有良好的性能,能够有效提高机械臂的操作效率和
视觉SLAM14精讲——三维空间刚体运动1.0
简介 第一份工作是一家比较大的机器人企业,被迫在AI视觉的基础上自学SLAM。一开始接触的就是vslam14讲,现在想把一些心得和基础知识分享一下。但是目前网络上有关视觉SLAM14讲挺多了,所以本系列不会重复书本中已经有的基本内容,也不一定按顺序发表。想要体现的还是一些更深层的理解和书本意外的一些知识。 三位空间刚体运动 前两章的内容都是一些基础背景知识以及专业名词解释,因此我选择
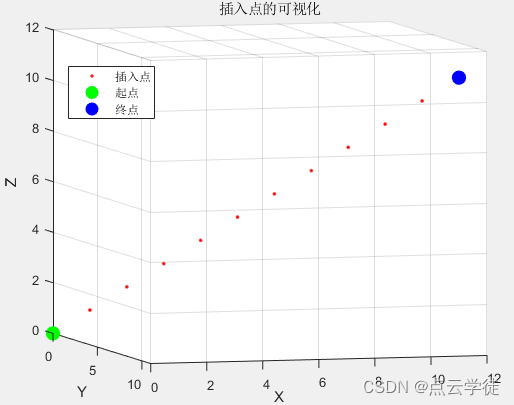
MATLAB 三维空间中在两点之间等间隔插入多个点 (67)
MATLAB 三维空间中在两点之间等间隔插入多个点 (67) 一、算法介绍二、算法实现1.代码2.结果 一、算法介绍 用于加密直线点云,具体为根据给定的直线端点,沿着该直线方向,插入多个点,从而加密。具体方法和效果如下所示: 二、算法实现 1.代码 代码如下(示例): % 定义两个点a = [0, 0,
unity计算三维空间下点到线,点到面,线到线,线到面,面到面最短距离的点的方法
通用的一个方法GetDistance,计算两个点的距离,不开平方 /// <summary>/// 获取两个点的距离,不开平方/// </summary>/// <param name="a"></param>/// <param name="b"></param>/// <returns></returns>public static float GetDistance(Vecto
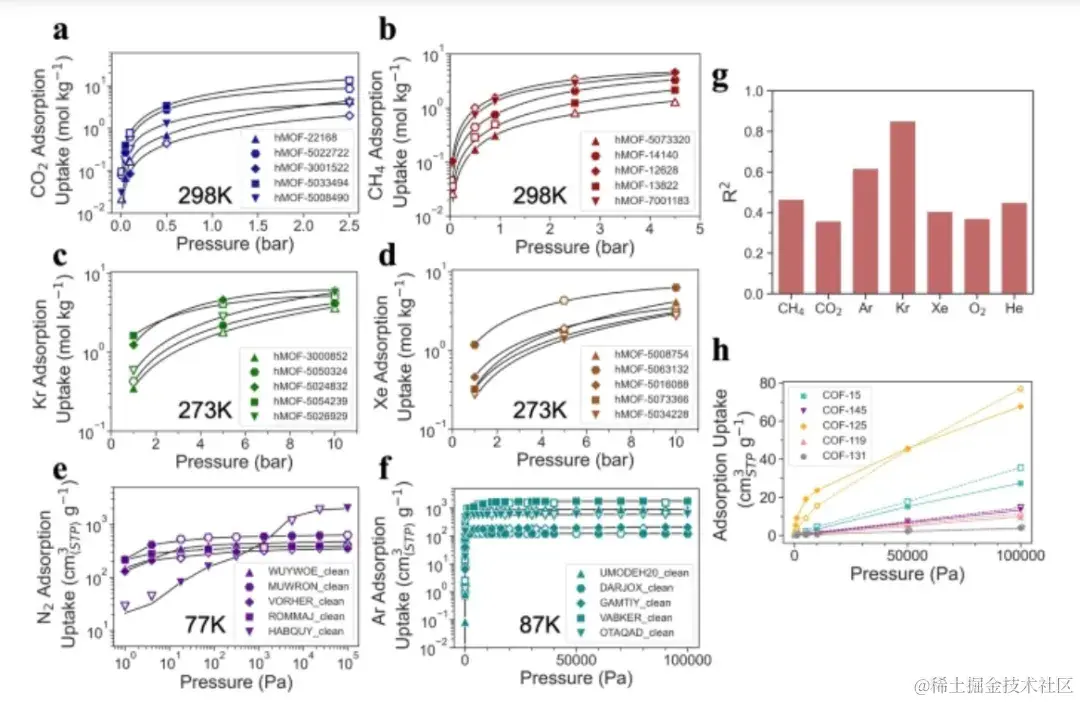
有效识别 63 万个三维空间构型,清华大学牵头发布 Uni-MOF 模型,预测 MOF 吸附能力
工业世界里,高纯气体被广泛应用于半导体制造、光纤生产、科学研究、医疗健康、环保能源等诸多领域。例如,半导体行业,高纯气体是芯片制造的关键原材料,直接影响着集成电路的性能和良率。 制备高纯气体的关键挑战便是气体分离,常见的气体分离方法有深冷法(精馏原理)、吸附法(分子极性**)、膜法(膜过滤)等。其中,金属有机框架 (MOFs) 由于具有高度有序的孔结构和可调节的孔径大小,在气体吸附存储与分离方面
ThingJS:十万多个三维空间模型请参考
数字孪生体属于信息空间的产物,而ThingJS提供的是信息可视化应用开发,与数字化未来无缝融合。 数字孪生体 产品数字孪生体是指产品物理实体的工作状态和工作进展在信息空间的全要素重建及数字化映射,是一个集成的多物理、多尺度、超写实、动态概率仿真模型,可用来模拟、监控、诊断、预测、控制产品物理实体在现实环境中的形成过程、状态和行为。 产品数字孪生体对应产品物理实体,一虚一实,我们称之为Thin
FlyControls 是 THREE.js 中用于实现飞行控制的类,它用于控制摄像机在三维空间中的飞行。
demo演示地址 FlyControls 是 THREE.js 中用于实现飞行控制的类,它用于控制摄像机在三维空间中的飞行。 入参: object:摄像机对象,即要控制的摄像机。domElement:用于接收用户输入事件的 HTML 元素,通常是渲染器的 DOM 元素。 出参: FlyControls 类本身没有直接返回出参,但通过修改传入的摄像机对象的位置和方向,从而影响场景中的摄
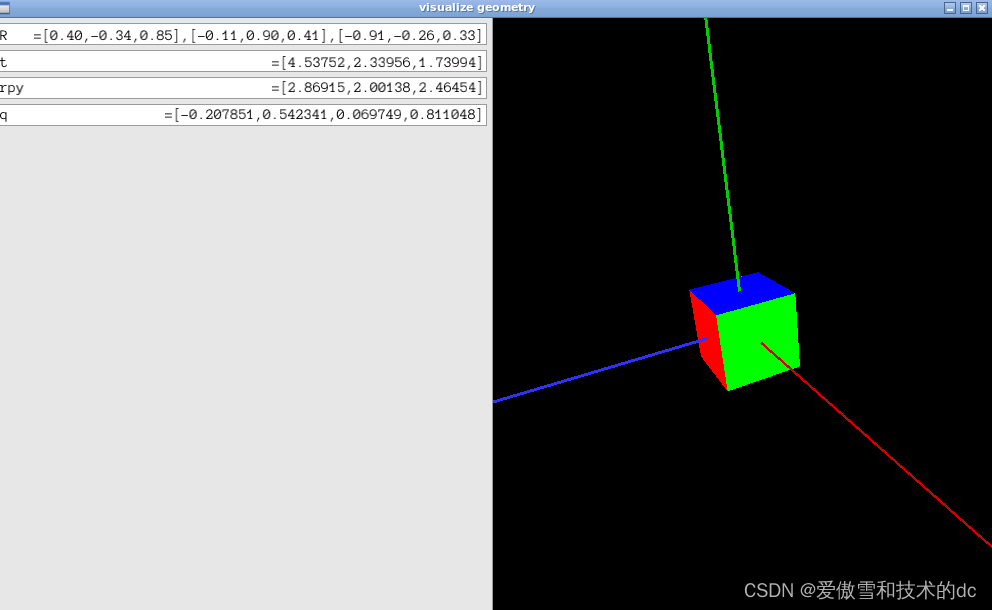
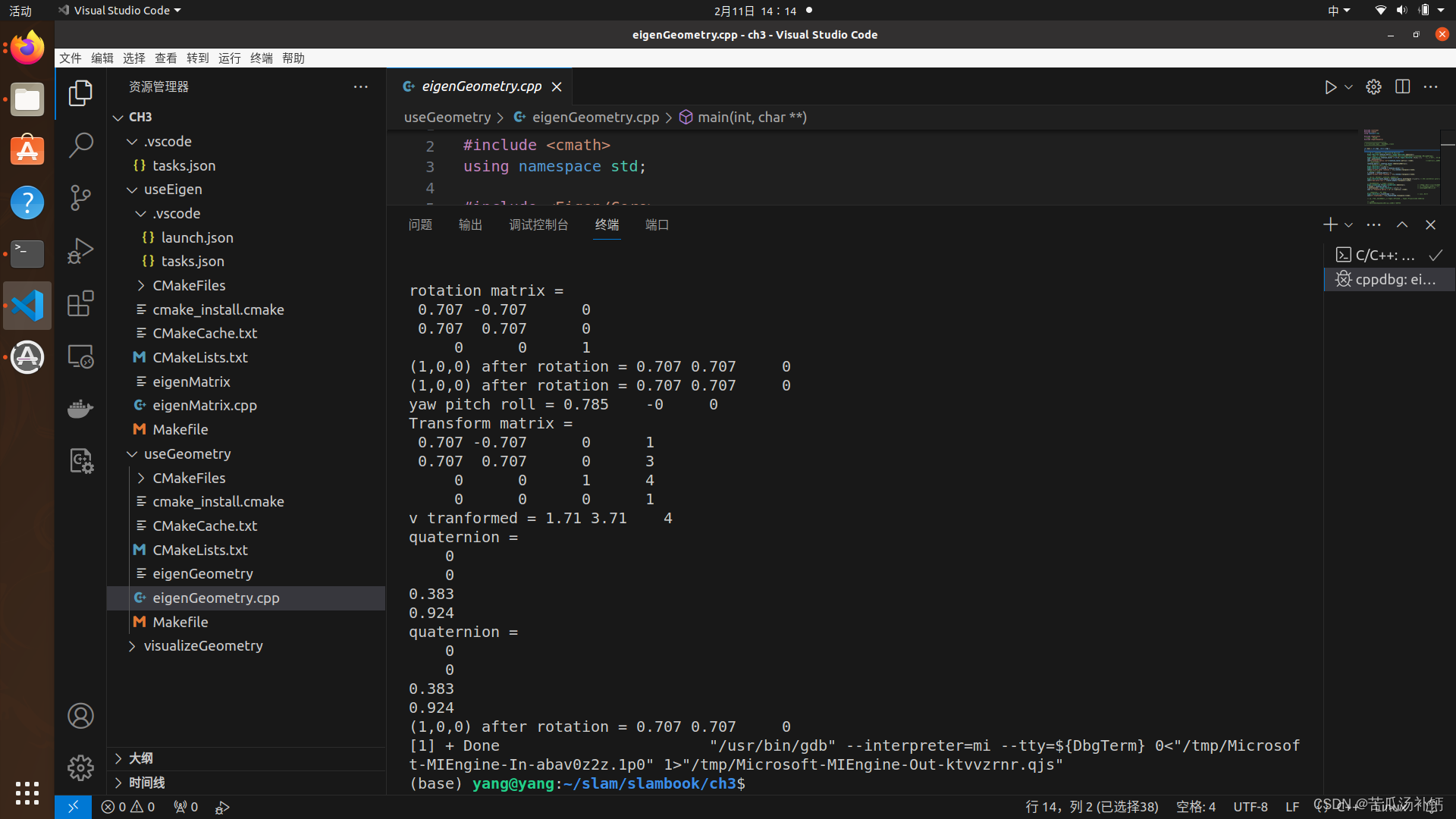
slam三维空间刚体运动及Eigen库的使用
1.理论部分 1.旋转矩阵 旋转矩阵有一些特别的性质。事实上,它是一个行列式为 1 的正交矩阵。反之,行 列式为 1 的正交矩阵也是一个旋转矩阵。所以,我们可以把旋转矩阵的集合定义如下: 由于旋转矩阵为正交阵,显然 RT 刻画了一个相反的旋转。 我们把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。 齐次坐标。它是射影几何里的概念。通过添加最后一维,我们用四个实数
matlab画三维空间劣弧,matlab 三维空间画图总结
matlab 三维画图总结 1.画函数的三维图,如:Z(X,Y)=2*X.*exp(-X.^2-Y.^2)+1; close all; [X,Y]=meshgrid(-2:0.5:2,-2:0.5:2);%生成坐标轴 Z=2*X.*exp(-X.^2-Y.^2)+1;%Z是X,Y的函数 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
海格里斯HEGERLS托盘搬运机器人四向车引领三维空间集群设备柔性运维
随着市场的不断迅猛发展变化,在物流仓储中,无论是国内还是海外,都对托盘式解决方案需求量很大。顾名思义,托盘式解决方案简单理解就是将产品放置在托盘上进行存储、搬运和拣选。 面对托盘式方案需求,行业中常见的方案是叉车式平库。这种方案本质上是一个人工仓库,往往需要配置叉车,雇一些叉车工人进行搬运。但这一方案依赖于大量人工,且存储密度不足,日益面临挑战。 软硬一体化产品体系增加
Direct3D学习笔记(四) 制作一个真正的三维空间
making our triangle three dimensional回头看看我们以前的程序,它看起来并不那么三维。我们只是在windows窗口中画了一个三角形而已,而这个用GDI是很容易做到的,现在我么那要做的就是怎么样画出一个物体来让他看起来比较三维化,而这些,很容易在我们已有的程序中进行改进而得到。如果你还记得,在早些时候当我们创造第一三角形的时候,我们使用了一种叫做转换匹配(tran
视觉SLAM十四讲学习笔记(二)三维空间刚体
哔哩哔哩课程连接:视觉SLAM十四讲ch3_哔哩哔哩_bilibili 目录 一、旋转矩阵 1 点、向量、坐标系 2 坐标系间的欧氏变换 3 变换矩阵与齐次坐标 二、实践:Eigen(1) 运行报错记录与解决 三、旋转向量和欧拉角 1 旋转向量 2 欧拉角 四、四元数 1 四元数的定义 2 四元数的运算 3 用四元数表示旋转 4 四元数到旋转矩阵的转换 五、
无人机在三维空间中的转动问题
前提 这篇博客是对最近一个有关无人机拍摄图像项目中所学到的新知识的一个总结,比较杂乱,没有固定的写作顺序。 无人机坐标系旋转问题 上图是无人机坐标系,绕x轴是翻滚(Roll),绕y轴是俯仰(Pitch),绕z轴是偏航(Yaw)。在初始位置,无人机坐标系和世界坐标系是对齐的,在坐标系中存在一个原始点 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0
三维空间两直线/线段最短距离、线段计算算法
设有两空间线段 $L_s$,其起点、终点坐标为$ s_0、s_1 $,方向向量$\vec u = s_1-s_0 $$L_t$,其起点、终点坐标为$ t_0、t_1 $,方向向量$\vec v = t_1-t_0 $记两线段对应的直线为$l_s、l_t$,采用向量表示法如下: $$l_s = s_0+c_s\cdot\vec u$$$$l_t = t_0+c_t\cdot\vec v$$当$0\
如何用C语言程序生成任意手性(即具有任意m和n值),任意长度的碳纳米管,并输出三维空间坐标呢?
如何用C语言程序生成任意手性(即具有任意m和n值),任意长度的碳纳米管,并输出三维空间坐标呢? 生成任意手性、任意长度的碳纳米管可以使用 Chirality Vector 和 Unit Vector 的概念来表示。Chirality Vector (n, m) 描述了碳纳米管的手性,其中 n 和 m 是整数,且满足 n ≥ m。Unit Vector 定义了碳纳米管轴向的方向。 下面是一个使用 C
刚体在三维空间的旋转-几种表达方式
三维空间的旋转(3D Rotation)是一个很神奇的东东:如果对某个刚体在三维空间进行任意次的旋转,只要旋转中心保持不变,无论多少次的旋转都可以用绕三维空间中某一个轴的一次旋转来表示。表示三维空间的旋转有多种互相等价的方式,常见的有欧拉角、旋转矩阵(DCM-方向余弦阵)、旋转向量、四元数等。本篇文章主要梳理一下这些表示方式及相互转换的方法。 1. 欧拉角(Euler Angle) 最直观的表
三维空间刚体运动4-3:四元数线性插值方法:Squad
三维空间刚体运动4-3:四元数线性插值方法:Squad 1. Squad的引出2. B e ˊ z i e r c u r v e B\acute{e}zier \space curve Beˊzier curve2.1 曲线的引出2.2 公式形式及动画演示 3. 样条3.1 样条由来3.2 样条曲线 4. 贝塞尔样条4.1 基本概念4.2 扩展:B样条曲线和非均匀有理B样条 5. de
三维空间刚体运动4-2:四元数线性插值方法:Slerp(详解证明)
三维空间刚体运动4-2:四元数线性插值方法:Slerp(详解证明) 1. 幂函数形式Slerp插值方法的引出2. 4D空间四元数夹角 VS 3D空间向量旋转变化量2.1 4D空间四元数夹角2.2 3D空间向量旋转变化量 3. 可视化插值曲线3.1 直接可视化图像3.2 角速度近似值的可视化3.3 插值曲线平滑性可视化 4. 平面线性插值方法:LinEuler,LinMat,Lerp和Nler
从零开始实现3D软光栅渲染器 (4) 三维空间变换
世界是3D的,显示器是2D,将三维空间的物体变换到二维空间,再到最终屏幕上成像的过程,在图形学中叫做3D渲染流水线。这个过程着实有点复杂了,让我们慢慢来,本节我们先介绍一些基本的空间变换知识。 这部分知识点非常重要,不管以后做游戏、仿真项目,还是其他图形应用,物体的空间变换是必须要理解的,因为很多实际的需求需要你自己分析,再去实现。就Unity来说吧,它已经把图形学中的矩阵、向量运算封装的相当易
python3 绘制三维空间圆的散点图
python 没有方便好用的直接画圆的方法,一般而言,都是使用参数方程画圆,要在三维空间画圆,可利用三维空间中圆的参数方程: { x ( θ ) = c 1 + r c o s ( θ ) a 1 + r s i n ( θ ) b 1 y ( θ ) = c 2 + r c o s ( θ ) a 2 + r s i n ( θ ) b 2 z ( θ ) = c 3 + r c o s
c++绘制三维空间圆的散点图
三维空间圆形式如下: 三维空间圆的参数方程: PCL绘制3D圆轨迹c++代码: //center 为圆心,normal 为圆法向量, Radius为半径pcl::visualization::PCLVisualizer::Ptr Plot3DCircle(pcl::PointCloud<pcl::PointXYZ>::ConstPtr cloud,pcl::PointXYZ center
二维空间与三维空间的姿态表示法
二维空间与三维空间的姿态表示法 一、2D空间姿态表示法二、3D空间姿态表示法2.1 三个数表示空间姿态问题 2.2 九个数表示空间姿态问题 2.3 四个数表示空间姿态 结语Reference 假设,你有志成为我空军某航空旅歼-20飞行员,但要想开好飞机,那就得锻炼身体,好好学习,因此,你刻苦学习专业知识,并梦想有一天,能真正演练编队飞行技术和空中作战战术,下面,未来的飞行员同志,在此
《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录 02 三维空间的刚体运动2.0 机器人位姿表述2.1 点和坐标系2.1.1 三维坐标系有关表述2.1.2 坐标系变换 2.2 旋转向量和欧拉角2.2.1 旋转向量2.2.2 欧拉角 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的计算2.3.3 四元数表示旋转2.3.4 四元数与其他旋转表示法的转换 2.4 相似、仿射、射影变换 02 三维空间的刚体运动
04-附注 三维空间中的线性变换
附注 三维空间中的线性变换 三维空间线性变换 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 三维空间线性变换 图1 绕y轴旋转90° 绕y轴旋转90°后,各基向量所在的坐标如图1所示。用旋转后的各基向量作为矩阵的列,就得到变换矩阵。变换矩阵就是对原向量就是缩放、旋转。
机器人基础知识(1.2-1.2.1)三维空间位姿描述(旋转)
三维情况是上一节的二维情况(二维空间位姿描述)的延伸。在二维坐标系上增加一个额外的坐标轴即可,通常用z表示,它同时与x轴和y轴正交。z轴的方向服从右手规则,并构成右手坐标系。与各坐标轴平行的单位向量记作 x ^ \hat{x} x^、 y ^ \hat{y} y^和 z ^ \hat{z} z^: z ^ = x ^ × y ^ , x ^ = y ^ × z ^ , y ^ = z ^ ×