本文主要是介绍C++之Eigen库基本使用(下),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、常见变换
Eigen::Matrix3d //旋转矩阵(3*3)
Eigen::AngleAxisd //旋转向量(3*1)
Eigen::Vector3d //欧拉角(3*1)
Eigen::Quaterniond //四元数(4*1)
Eigen::Isometry3d //欧式变换矩阵(4*4)
Eigen::Affine3d //放射变换矩阵(4*4)
Eigen::Projective3d //射影变换矩阵(4*4)2、矩阵运算
MatrixXcf a = MatrixXcf::Random(3,3);
a.transpose(); # 转置
a.conjugate(); # 共轭
a.adjoint(); # 共轭转置(伴随矩阵)
// 对于实数矩阵,conjugate不执行任何操作,adjoint等价于transpose
a.transposeInPlace() #原地转置
Vector3d v(1,2,3);
Vector3d w(4,5,6);
v.dot(w); # 点积
v.cross(w); # 叉积
v.norm(); #求模
Matrix2d a;
a << 1, 2, 3, 4;
a.sum(); # 所有元素求和
a.prod(); # 所有元素乘积
a.mean(); # 所有元素求平均
a.minCoeff(); # 所有元素中最小元素
a.maxCoeff(); # 所有元素中最大元素
a.trace(); # 迹,对角元素的和
// minCoeff和maxCoeff还可以返回结果元素的位置信息
int i, j;
a.minCoeff(&i, &j);3、 特殊矩阵
零阵:类静态成员函数Zero() # Eigen::Matrix3d covMat = Eigen::Matrix3d::Zero()
常量矩阵:Constant(rows, cols, value)
随机矩阵:Random()
单位矩阵:Identity()
归一化矩阵:normalize()4、求解线性方程Ax=b
常见的有三种: 1)三角分解法 (Triangular Factorization), 2)QR 分解法 (QR Factorization), 3)奇异值分解法 (Singular Value Decompostion) 4、 LLT分解 5、LDLT分解法
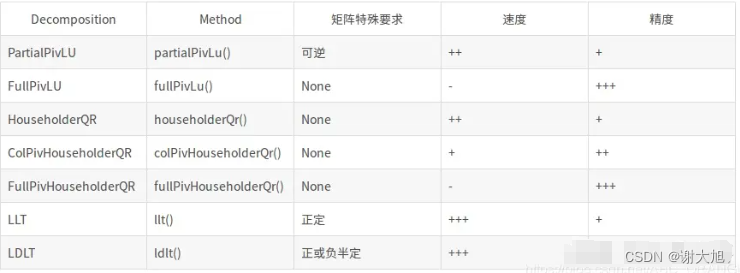
以上的函数可以求解线性方程组,请注意精度和速度
x = A.ldlt().solve(b)); // A sym. p.s.d. #include <Eigen/Cholesky>
x = A.llt() .solve(b)); // A sym. p.d. #include <Eigen/Cholesky>
x = A.lu() .solve(b)); // Stable and fast. #include <Eigen/LU>
x = A.qr() .solve(b)); // No pivoting. #include <Eigen/QR>
x = A.svd() .solve(b)); // Stable, slowest. #include <Eigen/SVD>
这篇关于C++之Eigen库基本使用(下)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




