differential专题

Python中差分进化differential_evolution的调用及参数说明

在场景应用中，要求我们的函数计算结果尽可能的逼近实际测量结果，可转化计算结果与测量结果的残差，通过最小化残差，便可求出最优的结果。但使用最小二乘等方法来计算时，常常会使迭代的结果显然局部最优点而导致结算错误。差分进化原理差分进化（Differential Evolution，DE）是一种基于群体差异的进化算法，其计算思想主要包括以下几个方面：一、初始化种群首先，随机生成一个初始种群

Differential Diffusion，赋予每个像素它应有的力量，以及在comfyui中的测试效果

🥽原论文要点首先是原论文地址：https://differential-diffusion.github.io/paper.pdf 其次是git介绍地址：GitHub - exx8/differential-diffusion 感兴趣的朋友们可以自行阅读。首先，论文开篇就给了一个例子：我们的方法根据给定的图片和文本提示，以不同的程度改变图像的不同区域。这种可控性允许我们再现

MACS bdgdiff: Differential peak detection based on paired four bedGraph files.

参考原文地址：[http://manpages.ubuntu.com/manpages/xenial/man1/macs2_bdgdiff.1.html](http://manpages.ubuntu.com/manpages/xenial/man1/macs2_bdgdiff.1.html) 文章目录一、MACS bdgdiff 简介DESCRIPTION 二、用法

微分方程（Blanchard Differential Equations 4th）中文版Section6.3

二阶线性方程 Laplace 变换求解在这一节中，我们将拉普拉斯变换方法扩展到二阶常系数强迫线性方程，即具有以下形式的方程： d 2 y d t 2 + p d y d t + q y = f ( t ) ， \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = f(t)， dt2d2y+pdtdy+qy=f(t)，其中 p p p 和 q q

微分方程（Blanchard Differential Equations 4th）中文版Section5.1

平衡点分析从第3章的工作中，我们能够对线性系统的解有定性和解析的理解。不幸的是，非线性系统通常不容易使用我们开发的解析和代数技术来分析，但我们可以利用线性系统的数学来理解非线性系统在其平衡点附近的行为。 Van der Pol 方程为了说明如何分析平衡点附近解的行为，我们从一个简单但重要的非线性系统——Van der Pol 系统开始。回顾一下，Van der Pol 系统是： d x

微分方程（Blanchard Differential Equations 4th）中文版Section4.4

稳态的振幅和相位系统在本节中，我们回到方程 d 2 y d t 2 + p d y d t + q y = cos ⁡ ω t \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = \cos \omega t dt2d2y+pdtdy+qy=cosωt 用于周期性强迫的阻尼谐振子。我们的目标是建立解决方案行为与参数之间的定量关系——特别是决定强迫频率

微分方程（Blanchard Differential Equations 4th）中文版Section3.5

特殊情况: 重根和零特征值的线性系统在前面的三节中，我们讨论了线性系统 d Y d t = A Y \frac{dY}{dt} = AY dtdY=AY 其中 2 × 2 2 \times 2 2×2 矩阵 A A A 具有两个不同的非零实特征值或一对复共轭特征值。在这些情况下，我们能够使用特征值和特征向量来草绘 x y xy xy 相平面的解，绘制 x ( t ) x(t)

微分方程（Blanchard Differential Equations 4th）中文版Section2.3

阻尼谐振子在本节中，我们将描述一种解析技术，它适用于本书中最重要的模型之一——阻尼谐振子。这一二阶微分方程用于建模各种现象，如质量-弹簧系统、电路理论中的RLC电路，以及人体的血糖调节系统。例如，考虑汽车的悬挂系统。它可以平滑崎岖道路上的颠簸，并帮助保持轮胎与地面的接触。我们主要关注悬挂中的弹簧和减震器（见图2.34和2.35）。弹簧吸收由路面颠簸引起的力，并保持轮胎与道路接触。减震器由一

DPTree: Differential Indexing for Persistent Memory（VLDB 2019）

（一）研究目的实现崩溃一致性，减少 PM 写入，并保持优秀的读性能。（二）研究背景根据结构特性，现有的 PM 索引研究大致可以分为B+Tree based、Trie-based 和 hybrid(混合) 三种类型。B+Tree based 结构（例如 CDDS-Tree、wB+Tree、NVTree、FPTree、FASTFAIR）在索引更新的关键代码路径上的持久化原语的数量是次优的。

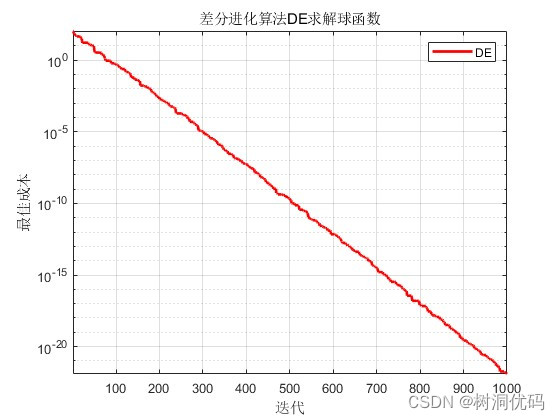
免费：差分进化算法（Differential Evolution, DE）原理及其Matlab代码，详细中文版！

差分进化算法（Differential Evolution, DE）原理及其Matlab代码，详细版!!! 差分进化算法是一种有效且简单的全局优化算法，适用于解决连续优化问题。由Storn和Price于1997年提出，以其简单的结构、易于实现的特性、少量的参数需求，以及对初始值选择的低敏感性而受到广泛应用。一、差分进化算法主要通过以下四个步骤进行： 1)种群初始化在算法开始时随机生成一

[足式机器人]Part4 南科大高等机器人控制课 Ch01 Linear Differential Equations and Matrix Exponential

本文仅供学习使用本文参考： B站：CLEAR_LAB 课程主讲教师： Prof. Wei Zhang 南科大高等机器人控制课 Ch01 Linear Differential Equations and Matrix Exponential 1. ODEs-Ordinary Differential Equations1.1 Dynamics of 2R linkage1.1.1

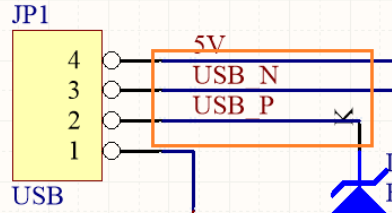
AD20中关于“Net(s) Not Found in Differential Pair”的解决方法

问题描述： Net(s) Not Found in Differential Pair：在差分对中找不到网络我们需要在原理图设计中需要添加差分对，已经遵循了_N _P 结尾，也添加了差分对标识符，但是转换到PCB时显示差分对报错解决方法： 1.先把所有的差分对符号全部删掉，先不用添加差分对符号从原理图转换一次PCB，此时没有报错提示 2.将第一次转换好的PCB保存好后，

基于差分进化算法（Differential Evolution Algorithm，DE）的移动边缘计算的任务卸载与资源调度研究（提供MATLAB代码）

一、优化模型介绍移动边缘计算的任务卸载与资源调度是指在移动设备和边缘服务器之间，将部分计算任务从移动设备卸载到边缘服务器，并合理分配资源以提高系统性能和降低能耗。在本文所研究的区块链网络中，优化的变量为：挖矿决策（即 m）和资源分配（即 p 和 f），目标函数是使所有矿工的总利润最大化。问题可以表述为： max ⁡ m , p , f F miner = ∑ i ∈ N ′ F i m

Differential

之前我有一篇《差分+前缀和》的学习笔记，记录了差分的思想和基本用法。这里就只记录灵神题单的刷题记录。 1. LC 1094 拼车我记得这是哪次每日一题来着，入门差分前缀和了。差分数组维护每站新增的乘客（当然数量可以是≤0的），每一项在上车对应位置加。下车对应位置减即可。 class Solution {public boolean carPooling(int[][] trips,

Differential Brands Group将以13.8亿美元收购利标品牌北美部门绝大部分业务

- 将创造北美领先的消费平台，产生超过23亿美元的营收洛杉矶--(美国商业资讯)--由Hudson、Robert Graham和SWIMS等一系列国际消费品牌组成的Differential Brands Group Inc.（以下简称“公司”或“Differential”）(NASDAQ:DFBG)今日宣布，公司已与香港上市公司利标品牌有限公司（香港联合交易所股票代码：787) (“G

【基础储备】Differential Privacy 基础知识储备

onion routing, online tracking, privacy policies, genetic privacy, social networks 传统隐私保护方法概览 k-anonymityk-mapl-diversityδ-presence Why differential privacy is awesome We no longer need attack m

【基础储备】Differential Privacy 基础知识储备之 privacy book

privacy loss 的定义： the p r i v a c y l o s s privacy \, loss privacyloss incurred by observing ξ \xi ξ is (ε-δ)-差分隐私的复合性质：加性切诺夫界、乘性切诺夫界： Azuma不等式：斯特林公式： Laplace机制的 bound ： u

【论文记录】Deep Learning with Differential Privacy

差分隐私的隐私开销计算（注: 实际上前面的PPT内容都是论文中的details）记录几条需要搞清楚的疑问 Introduction右边的三条PDF中的几条标记Theorem 1紧跟着的一段中如何根据the strong composition theorem得出 σ \sigma σ的渐进下界？介绍到the strong composition theorem时,文章中标注的参考文献是[2

【论文记录】Input Perturbation: A New Paradigm between Central and Local Differential Privacy

算法&基本思想 By line 7 in Algorithm 1, it can be seen that the noise added to the original data affects the gradient. (adds noise to original data instances, leading perturbation on the gradient and ev

Multi-Grade Deep Learning for Partial Differential Equations

论文阅读：Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Bur