【基础储备】Differential Privacy 基础知识储备之 privacy book

• privacy loss 的定义 ： the $privacyloss$ incurred by observing $\xi$ is
  
  
  
  

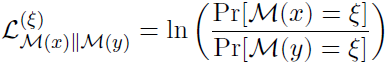
• (ε-δ)-差分隐私的复合性质 ：
  
  
  
  

• 加性切诺夫界、乘性切诺夫界 ：
  
  
  
  

• Azuma不等式 ：
  
  
  
  

• 斯特林公式 ：
  
  
  
  

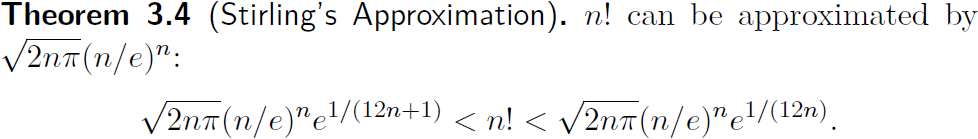
• Laplace机制的 bound ：
  
  
  
  

• utility function ：
  utility function $u:{\mathbb{N}}^{|\mathcal{X}|}\times \mathcal{R}\to \mathbb{R}$, which maps database/output pairs to utility scores.
  OPT${}_u(x)=$ max${}_{r\in \mathcal{R}}u(x,r)$ denote the maximum utility score of any element $r\in \mathcal{R}$ with respect to database $x$.
  
  
  

• 指数机制的 bound ：
  
  
  
  
  

• 高斯机制 ：
  
  更多详情见 The Gaussian Mechanism.pdf
  注：Gaussian Mechanism相较于Laplacian Mechanism有一个理论上的disadvantage,详见${\mathcal{P}}_{53}$
  
  
  

• Composition theorems ：
  
  
  
  

• 斯特林公式 ：

Reference

C. Dwork and A. Roth. The algorithmic foundations of differential privacy. Foundations and Trends in Theoretical Computer Science, 9(3{4):211{407, 2014.