本文主要是介绍免费:差分进化算法(Differential Evolution, DE)原理及其Matlab代码,详细中文版!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
差分进化算法(Differential Evolution, DE)原理及其Matlab代码,详细版!!!
差分进化算法是一种有效且简单的全局优化算法,适用于解决连续优化问题。由Storn和Price于1997年提出,以其简单的结构、易于实现的特性、少量的参数需求,以及对初始值选择的低敏感性而受到广泛应用。
一、差分进化算法主要通过以下四个步骤进行:
1)种群初始化
在算法开始时随机生成一个初始种群,每个个体代表问题空间中的一个潜在解。种群大小是预设的,并在进化过程中保持不变。
2)变异操作
对于种群中的每一个个体,随机选择三个不同的个体(a, b, c),并生成一个新的个体(v)使用下述变异策略:v = a + F *(b - c)其中,F是差分权重,是控制变异幅度的超参数,通常设置在0到2之间。
3)交叉操作
- 对变异后的个体和当前种群中的个体执行交叉操作,生成试验个体。通过交叉操作增加种群的多样性,通常使用均匀交叉,每个基因位的交叉概率由超参数交叉率(CR)控制。
4)选择操作
比较每个试验个体与当前种群中相对应的个体,若试验个体的适应度更好,则在种群中替换相应的个体,否则保持原个体不变。这确保了种群的适应度逐渐变好(一般是越小越好,当然也可以越大越好,根据目标函数设置)。
二、差分进化算法的参数
差分进化算法的性能很大程度上依赖于参数设置,主要参数包括:
种群大小:影响搜索空间的覆盖程度及算法的计算复杂度。
差分权重F:控制变异步骤中的缩放比例,影响算法平衡全局搜索与局部搜索的能力。
交叉率CR:控制交叉步骤中的基因交换程度,较高的CR可增加种群多样性。
三、应用与局限
差分进化算法因其简单高效,在许多实际问题中得到应用,如数值优化、图像分割、参数估计、优化设计等。然而,它也有局限性,如可能在局部最优解附近停滞,对某些问题可能需要特定的变异与交叉策略来提高效率。实践是学习差分进化算法最好的方式。尝试应用它解决一些标准的优化问题,比如函数最小化,有助于深入理解其工作原理及参数调整方法。
四、Matlab代码
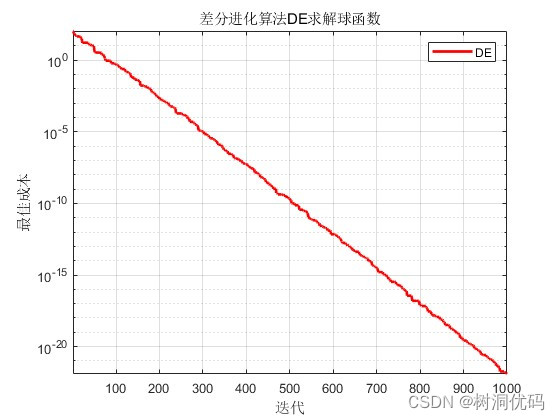
以最简单的球函数最小化为例,求解的Matlab代码如下,复制到matlab即可运行:
clc;
clear;
close all;%% 问题定义
CostFunction=@(x) Sphere(x); % 代价函数, 以经典的球函数为例,最小化目标函数nVar=20; % 决策变量的数量VarSize=[1 nVar]; % 决策变量矩阵大小VarMin=-5; % 决策变量的下界
VarMax= 5; % 决策变量的上界%% 差分进化参数
MaxIt=1000; % 最大迭代次数nPop=50; % 种群大小F_min=0.2; % 缩放因子F的下界
F_max=0.8; % 缩放因子F的上界pCR=0.2; % 交叉概率%% 种群初始化
empty_individual.Position=[];
empty_individual.Cost=[];BestSol.Cost=inf;pop=repmat(empty_individual, nPop, 1);for i=1:nPoppop(i).Position=unifrnd(VarMin, VarMax, VarSize);pop(i).Cost=CostFunction(pop(i).Position);if pop(i).Cost < BestSol.CostBestSol=pop(i);end
endBestCost=zeros(MaxIt, 1);%% 差分进化主循环
for it=1:MaxItfor i=1:nPopx=pop(i).Position;% 随机选择三个个体A=randperm(nPop);A(A==i)=[];a=A(1);b=A(2);c=A(3);% 变异操作F=unifrnd(F_min, F_max, VarSize);y=pop(a).Position + F .* (pop(b).Position - pop(c).Position);y = max(y, VarMin);y = min(y, VarMax);% 交叉操作z=zeros(size(x));j0=randi([1 numel(x)]);for j=1:numel(x)if j==j0 || rand<=pCRz(j)=y(j);elsez(j)=x(j);endendNewSol.Position=z;NewSol.Cost=CostFunction(NewSol.Position);% 选择操作if NewSol.Cost < pop(i).Costpop(i)=NewSol;if pop(i).Cost < BestSol.CostBestSol=pop(i);endendend% 更新最佳成本BestCost(it)=BestSol.Cost;% 显示迭代信息(已注释)disp(['迭代 ', num2str(it), ' 次:最佳成本 = ', num2str(BestCost(it))]);
end%% 显示结果
figure;
semilogy(BestCost, '-r','LineWidth', 2);
xlabel('迭代');
ylabel('最佳成本');
title('差分进化算法DE求解球函数')
grid on;
axis tight
legend('DE')function z=Sphere(x)z=sum(x.^2);end运行结果如下:
这篇关于免费:差分进化算法(Differential Evolution, DE)原理及其Matlab代码,详细中文版!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







