【论文记录】Deep Learning with Differential Privacy

• 差分隐私的隐私开销计算 （注: 实际上前面的PPT内容都是论文中的details）

记录几条需要搞清楚的疑问

• Introduction右边的三条
• PDF中的几条标记
• Theorem 1紧跟着的一段中如何根据the strong composition theorem得出$\sigma$的渐进下界？
• 介绍到the strong composition theorem时,文章中标注的参考文献是[24], 但此文中并没有the strong composition theorem的概念。

The Moments Accountant

privacy loss random variable 的传统定义是：${\mathcal{L}}_{\mathcal{M},D_1,D_2}(O)=\ln \frac{\mathbb{P}\left[\mathcal{M}(D_1)=O\right]}{\mathbb{P}\left[\mathcal{M}(D_2)=O\right]}$
但本文中的定义在其中多添加了一条 auxiliary input aux 如下：

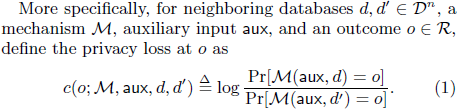
根据后续给出的定理及证明过程, 此 aux 指代的是 : 计算 $Pr[{\mathcal{M}}_i(d)=o_i]$ 时的已知条件 $({\mathcal{M}}_1,...,{\mathcal{M}}_{i-1})=(o_1,...,o_{i-1})$
这是由于本文采用的 design pattern 是 update the state by sequentially applying differentially private mechanisms. This is an instance of adaptive composition.
根据 privacy loss 随机变量 $c(o;\mathcal{M},aux,d,d^{\prime })$
再定义 ${\alpha }_{\mathcal{M}}(\lambda ;aux,d,d^{\prime })$ 为$c(o;\mathcal{M},aux,d,d^{\prime })$的矩量母函数的对数值。${\alpha }_{\mathcal{M}}(\lambda )=\underset{aux,d,d^{\prime }}{\max }{\alpha }_{\mathcal{M}}(\lambda ;aux,d,d^{\prime })$ 。于是有定理 :

本文用上述定理$1$来bound ${\alpha }_{{\mathcal{M}}_i}(\lambda )$ , 再利用被bound的${\alpha }_{\mathcal{M}}(\lambda )$和定理$2$来计算$\delta$
my id : 根据上述这个定理$2$的证明过程, 本文的作者是把 $\delta$ 定义为了 $Pr[c(o)\ge \epsilon ]$ 的值, 但实际上此 $\delta$ 可以更小 …?
定理$1$的证明过程如下 :
\quad\quad

其他阅读顺序

22 基础铺垫
8,53 本文是他们的跟进、延伸
+++++++++++++++++++++++++++++++++++++++++++++++++++++
24 关于strong composition theorem
+++++++++++++++++++++++++++++++++++++++++++++++++++++
42 关于privacy accountant
44 关于The moments accountant的来源: Renyi Differential Privacy
+++++++++++++++++++++++++++++++++++++++++++++++++++++
25 differentially private PCA algorithm
+++++++++++++++++++++++++++++++++++++++++++++++++++++
9 在 Moments accountant 中用到的 the privacy amplification theorem
+++++++++++++++++++++++++++++++++++++++++++++++++++++
58 用convex empirical risk minimization对数据集MNIST的实验精度

11 作为22的推广
23 advanced composition theorems and their refinements