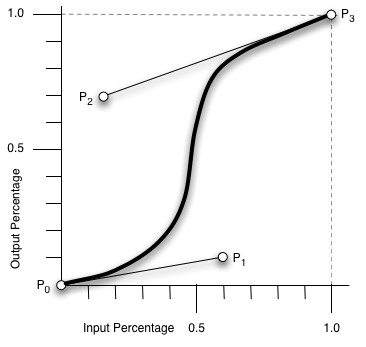
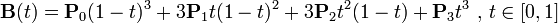bezier专题
Bezier曲线曲面--拟合技术
Bezier曲线曲面–拟合应用 1.Bezier曲线 1.1.Bezier曲线的定义 给定一组控制点 P_0, P_1, …, P_n,其中 n 是曲线的阶数,Bezier曲线的参数方程可以表示为: B ( t ) = ∑ i = 0 n P i b i , n ( t ) , t ∈ [ 0 , 1 ] B(t) = \sum_{i=0}^{n} P_i b_{i,n}(t), \qua
计算机图形学-基于OpenGL的绘制Bezier曲线
计算机图形学-基于OpenGL的绘制Bezier曲线 本实验集成开发环境为vs2013,基于OpenGL。 实验内容 根据Bezier曲线的定义,绘制Bezier曲线段。自己编程实现Bernstain基函数,然后在曲线上采集200个点,连成拆线段绘制。 预备知识 P(t)=∑i=0nPiBi,n(t),t∈[0,1] P(t)=\sum_{i=0}^n P_{i} B_{i,n}
探索CSS中的贝塞尔曲线cubic-bezier()函数:掌握自定义动画曲线的艺术
在CSS动画的世界里,平滑而自然的过渡效果是提升用户体验的关键。传统的线性或简单缓动效果有时无法满足复杂动画的需求,这时cubic-bezier()函数便大放异彩,它赋予开发者无限创意,让动画曲线随心所欲地定制。本文将深入解析cubic-bezier()的工作原理、使用方法、以及如何通过代码示例来实现那些令人惊艳的动画效果。 什么是cubic-bezier()函数? cubic-bezier(
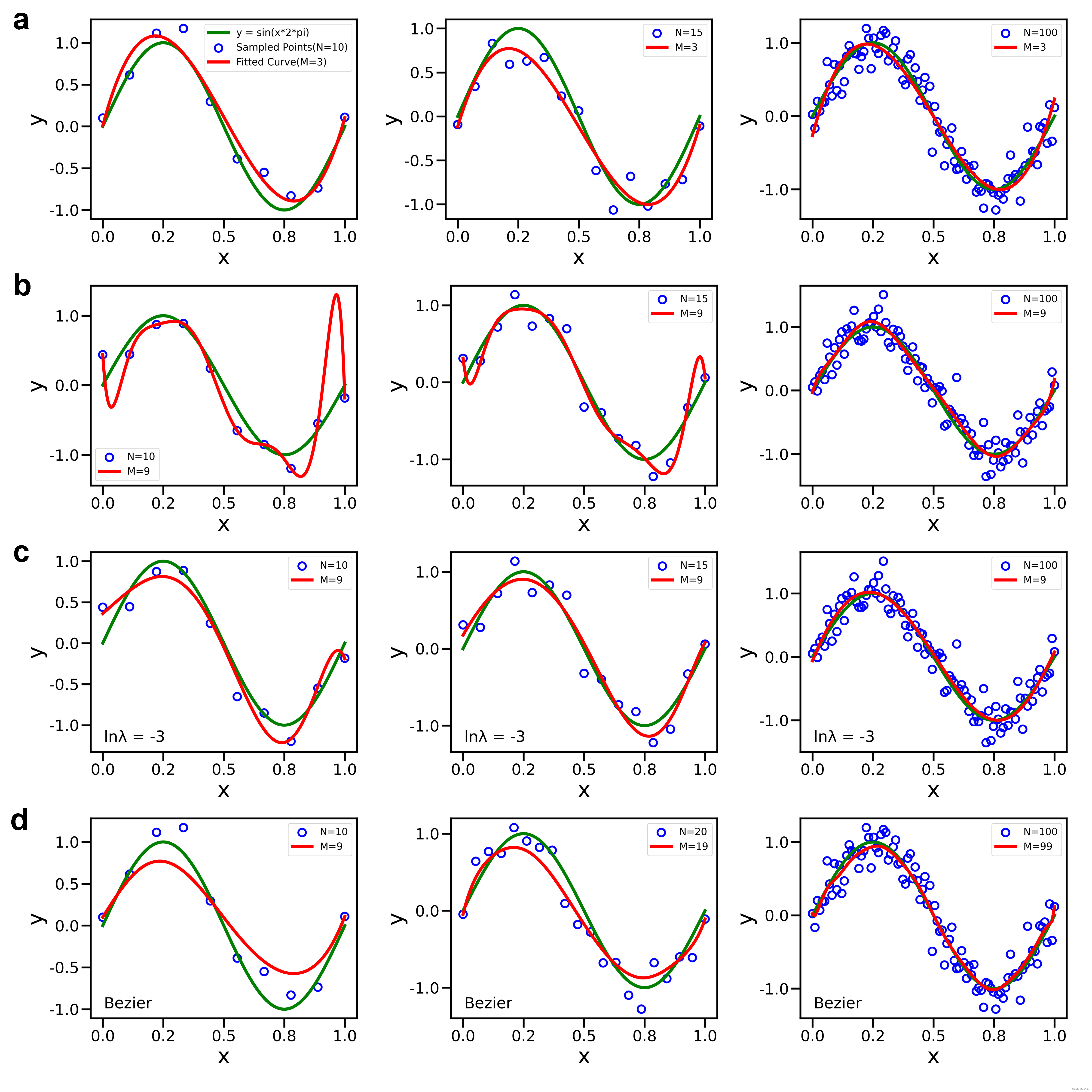
多项式和Bezier曲线拟合
目录 1. 多项式拟合2. Bezier曲线拟合3. 源码地址 1. 多项式拟合 在曲线拟合中,多项式拟合方法的性能受到三个主要因素的影响:采样点个数、多项式阶数和正则项。 采样点个数 N N N:从Figure 1中可以看出较少的采样点个数可能导致过拟合(overfitting)问题,即拟合曲线过于贴合训练数据,但在新数据上的泛化能力较差。而较多的采样点个数可以提供更
图像算法研究---Bezier曲线详解
关于Bezier曲线,本人做个简单的几笔,纯粹是个人笔记,针对上一篇博客http://blog.csdn.net/trent1985/article/details/51396665进行一个知识补充。 1,Bezier曲线的定义 在给定空间n+1个点P0,P1,...Pn,称下列参数曲线为n次的Bezier曲线: 其中,是Bernstein基函数,即 一般称折线P0,P1,..
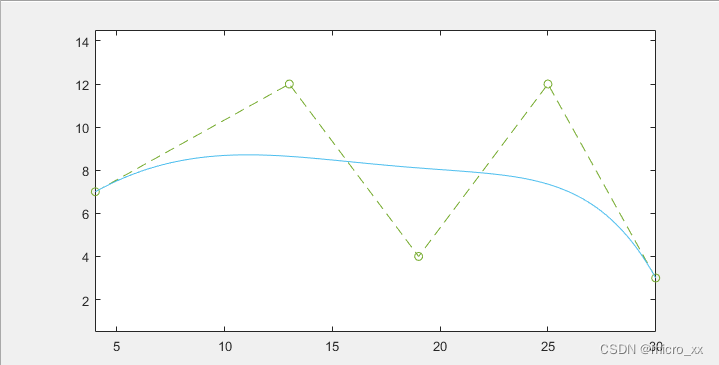
Bezier曲线的绘制 matlab
式中: 称为基函数。 。 因为n表示次数,点数为n+1,显然i表示第i个控制点。 显然在Matlab中可以同矩阵的形式来计算C(u)。 关键代码为: clcclear% 假设控制点P取值为:P = [4,7;13,12;19,4;25,12;30,3]; % 因此:n = 4;i = (0:n);Bcof_temp = factorial(n)./(factorial
Bezier曲线反求控制点
Bezier曲线反求控制点 做曲线拟合的时候,往往希望拟合的曲线通过数据点,这个推导一下Bezier曲线控制点的计算过程. 曲线公式 曲 线 : C ( u ) = ∑ i = 0 n B n , i ( u ) P i 基 函 数 : B n , i = n ! i ! ( n − i ) ! u i ( 1 − u ) n − i 曲线:C(u) = \sum^n_{i=0}B_{n,
bezier曲线拟合椭圆弧线
椭圆弧线用bezier曲线拟合 。 先计算出 椭圆中心 起始角度 旋转角度 S t e p 1 : C o m p u t e ( x 1 ′ , y 1 ′ ) Step 1: Compute(x'_1, y'_1) Step1:Compute(x1′,y1′) ( x 1 ′ y 1 ′ ) = ( cos φ sin φ − sin φ cos φ ) ⋅ ( x
计算机图形学(七)Bezier(贝塞尔)曲线讲解与源代码
源码下载:点我下载 “贝赛尔曲线”是由法国数学家Pierre Bézier所发明,由此为计算机矢量图形学奠定了基础。它的主要意义在于无论是直线或曲线都能在数学上予以描述。 算法的基本原理: 贝塞尔曲线贝塞尔曲线是计算机图形图像造型的基本工具,是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点(起始点、终止点以及两个相互分离的中间点)来创造、编辑图形。其中起重要作用的是位于曲
贝塞尔曲线(Bezier Curve)原理、公式推导及matlab代码实现
目录 参考链接 定义 直观理解 公式推导 一次贝塞尔曲线(线性公式) 二次贝塞尔曲线(二次方公式) 三次贝塞尔曲线(三次方公式) n次贝塞尔曲线(一般参数公式) 代码实现 参考链接 贝塞尔曲线(Bezier Curve)原理及公式推导_bezier曲线-CSDN博客 贝塞尔曲线(Bezier Curve)原理、公式推导及matlab代码实现-CSDN博客 贝塞
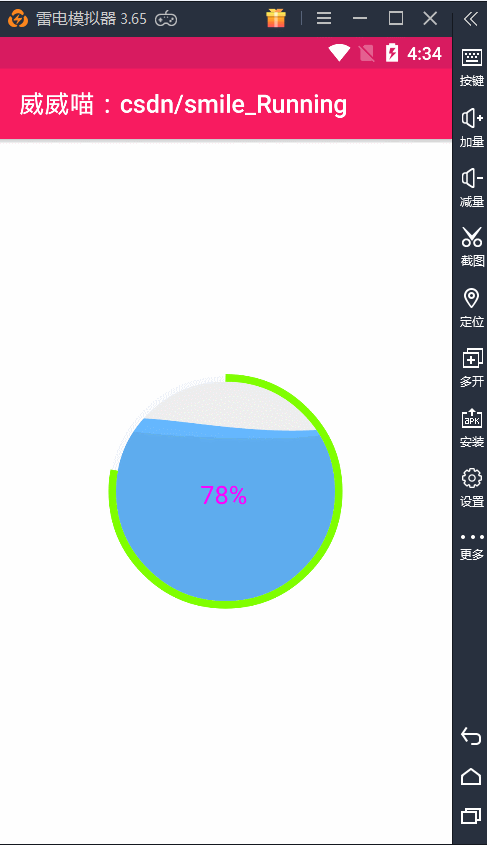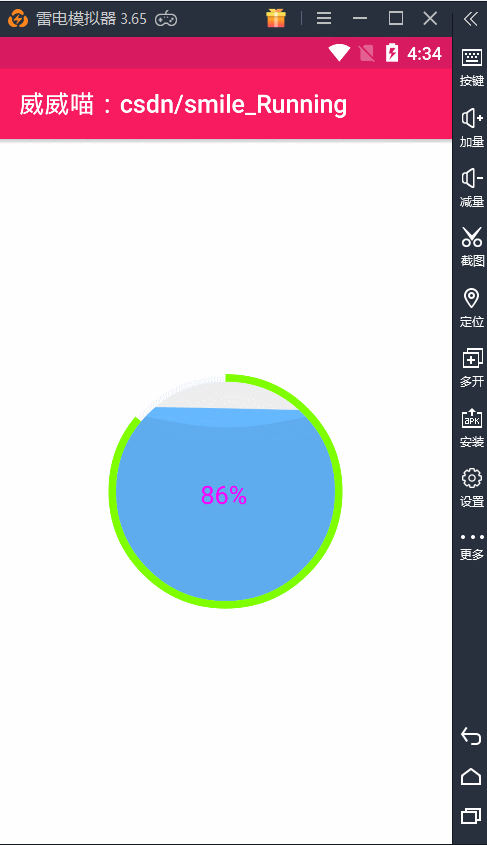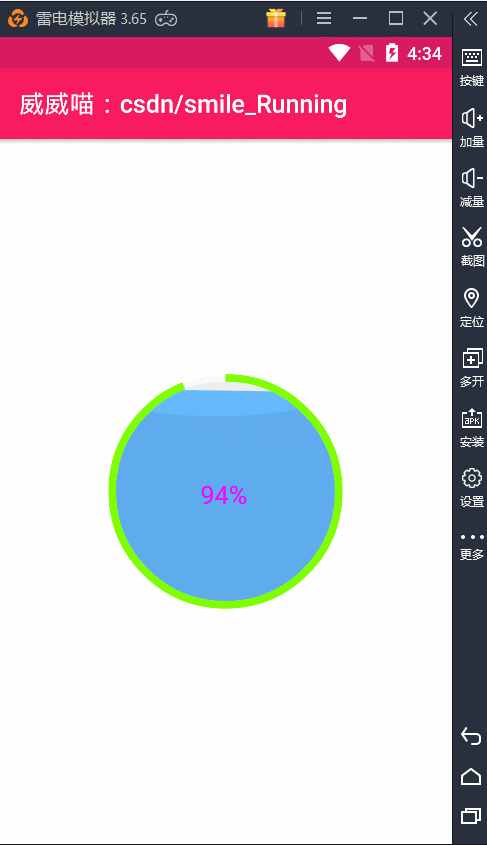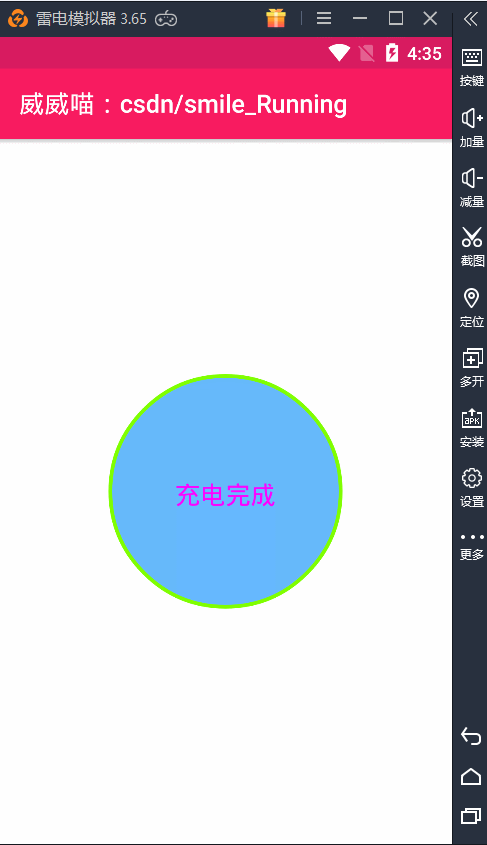
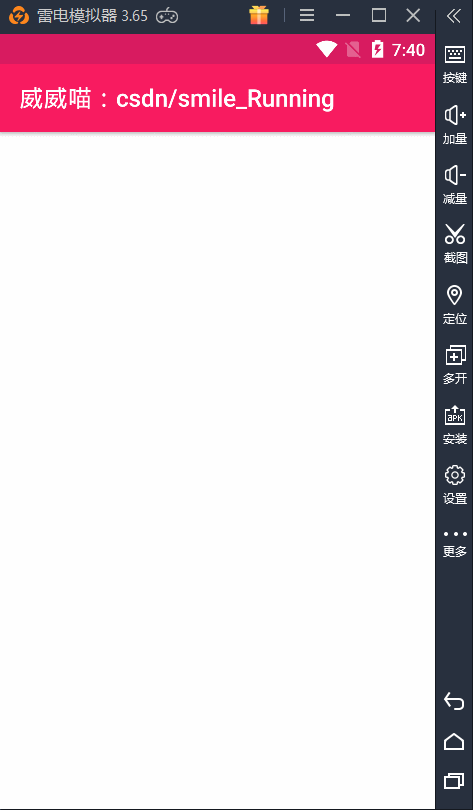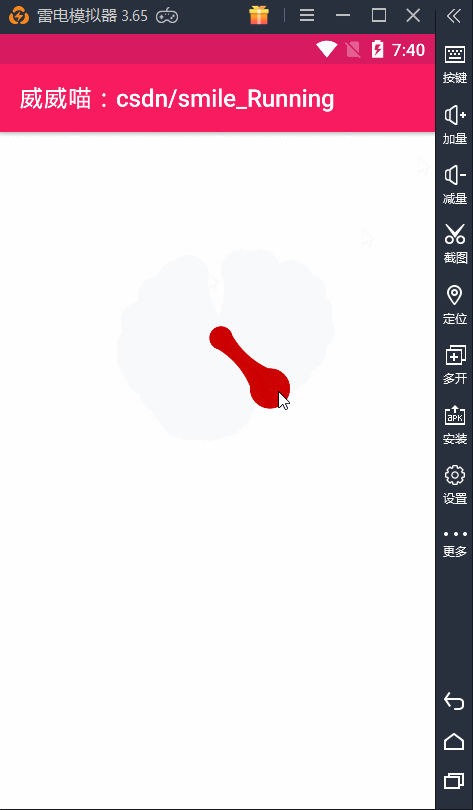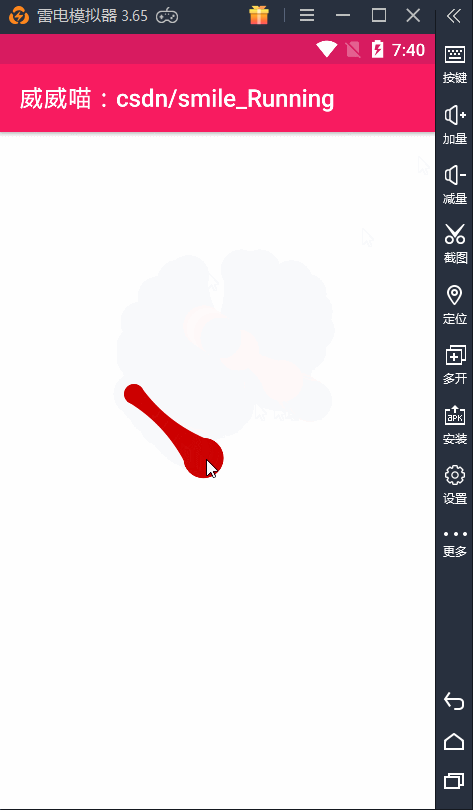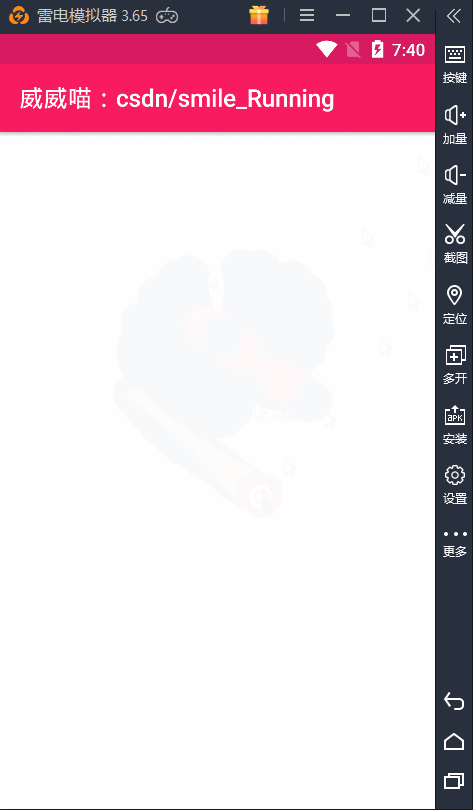
贝塞尔曲线(Bezier)之水波纹的手机充电动画效果(一)
博主声明: 转载请在开头附加本文链接及作者信息,并标记为转载。本文由博主 威威喵 原创,请多支持与指教。 本文首发于此 博主:威威喵 | 博客主页:https://blog.csdn.net/smile_running 博主这几天一直在搞贝塞尔曲线(Bezier)动画的研究,虽然我的数学不太好,但是也勉勉强强能够看懂懂贝塞尔曲线的公式,套用还是很简单的。前几次搞了几个贝塞尔
贝塞尔曲线(Bezier)之 QQ 消息拖拽动画效果
博主声明: 转载请在开头附加本文链接及作者信息,并标记为转载。本文由博主 威威喵 原创,请多支持与指教。 本文首发于此 博主:威威喵 | 博客主页:https://blog.csdn.net/smile_running 这几天突然发现 QQ 的消息拖拽动画效果还挺不错的,以前都没去留意它,这几看了一点关于贝塞尔曲线的知识,这不刚好沙场练兵。于是从昨天开始呢,我就已经开始补点
Bezier曲线的原理 及 二次Bezier曲线的实现
原文地址:http://blog.csdn.net/jimi36/article/details/7792103 Bezier曲线的原理 Bezier曲线是应用于二维图形的曲线。曲线由顶点和控制点组成,通过改变控制点坐标可以改变曲线的形状。 一次Bezier曲线公式: 一次Bezier曲线是由P0至P1的连续点,描述的一条线段 二次Bezier曲线公式
【iOS-Cocos2d游戏开发之十三】CCSprite利用Bezier(贝塞尔)抛物线并同时播放两个Action动作!...
本站文章均为 李华明Himi 原创,转载务必在明显处注明: 转载自【黑米GameDev街区】 原文链接: http://www.himigame.com/iphone-cocos2d/480.html 如果我们想实现让CCSprite进行抛物线运动的话,那么我想童鞋们首先会想到利用Box2d或者其他物理引擎去为CCSprite创建物理世界中对应的刚体进行实现,但是反过来想,对于不熟悉Box2d
双三次Bezier曲面
直接上图 /** @Name:双三次Bezier曲面* @Date:2023/3/11* @author:twj*//** 难点:①定义存放曲面的点的数组 或 结构体②选取u v方向 如从Bezier曲线 到 Bezier曲面 由一维到二维是怎么变化的③用什么来存储曲面上的点???那么又如何知道曲面上的点的个数,然后才能定义出数组存储面上的点* 总结
Bezier曲线与曲面(2)
导读: 2.三角域上的Bernstein基 单变量的n次的Bernstein基由的二项式展 开各项组成。双变量张量积的Bernstein基由两个单变量的Bernstein基各取 其一的乘积组成。而定义在三角域上的双变量n次的Bernstein基由 的展开式各项组成。 Bernstein基函数:
具有形状参数的新型广义混合三角贝齐尔样曲线(GHT_Bezier_curves) matlab实现
具有形状参数的新型广义混合三角贝齐尔样曲线 一、n维 GHT-Bernstein 基函数1、定义2、性质: 二、基函数的matlab程序实现1、程序:2.2 基函数图像 三、n维GHT-Bézier曲线(GHT-Bézier Curves of Degree n)相应程序:相应结果:注:得到的曲线应该满足凸包性质,但是有几个参数得到的曲线不在控制多边形里面(如b图中红色曲线),程序检查了几遍
贝塞尔曲线工具css,cubic-bezier贝塞尔曲线css3动画工具
今天在一本叫《HTML5触摸界面设计与开发》上看到一个做弹跳球的复杂动画效果,首先加速下降,停止,然后弹起时逐渐减速。是用cubic-bezier贝塞尔曲线来完成的。所以特地去学习了一下关于cubic-bezier贝塞尔曲线。 cubic-bezier比较少用,因为PC端中,有浏览器不兼容。但是手机端中,可以使用并带来炫酷的动画及体验。 cubic-bezier是贝塞尔曲线中的绘制方法。 css
MFC绘制Bezier曲面拼接圆
MFC绘制Bezier曲面拼接圆 理论算法与代码参考《计算几何算法与实现》–孔令德 下面给出绘制代码: 1、在上一篇文章的代码基础上,继续进行添加,地址链接 2、添加描述曲面片的数据类CPatch #pragma onceclass CPatch{public:CPatch(void);~CPatch(void);public:int pNumber;//表面顶点数in
animation属性之纯css3实现曲线运动——贝塞尔曲线(cubic-bezier)
animation: name duration timing-function delay iteration-count direction fill-mode play-state; (关键帧名称,持续时间,速度曲线,延迟时间,动画次数,是否反向,完成状态,运行|暂停) animation-name 关键帧名称 @keyframes name { } (1)关键帧的声明只有两种:(from