双三次Bezier曲面

2023-10-29 23:50
文章标签 三次 曲面 bezier

本文主要是介绍双三次Bezier曲面，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

直接上图

/*
* @Name:双三次Bezier曲面
* @Date:2023/3/11
* @author:twj
*/
/*
* 难点：①定义存放曲面的点的数组 或 结构体②选取u v方向 如从Bezier曲线 到 Bezier曲面 由一维到二维是怎么变化的③用什么来存储曲面上的点？？？那么又如何知道曲面上的点的个数，然后才能定义出数组存储面上的点* 总结：①设置16个控制点的数组 一开始想到一维数组+结构体  不方便，转三维数组
*        ②存放Bezier曲面的点的问题：先是思考如何在计算出Bezier曲线上的点的问题，主要运用到n次Beizer曲线
*            的定义式，当有四个控制点时候，为三次Bezier曲线，双三次则为二维的。
*            数组定义时候要明白一个道理，（u,v）  （u,v） （u,v） 的变化形式，重要的说三遍
*            **从0到1.0，每次+0.1 那么在一条Bezier曲线上就有11个点 在一个面上 两个gor循环就有11*11个点**
*        ③关于精度的问题：
*            不知道是不是计算机的问题，当我的（u,v）选取float时候绘画的图形出错，而使用double时候才成功，float u=o.double u=0.0???
*            其实，这里设计到计算机硬件的知识：（x86 ）
*                浮点运算都是以双精度进行的，即使只有float的运算，也要先转换成double型再算的，所以doublex型比float型要快一点。
*        ④关于OpenGL的API的调用：
*            glFlush()搭配glutInitDisplayMode(GLUT_RGBA | GLUT_SINGLE);
*            glutSwapBuffers()搭配glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE);
*            
*            因为API的问题，搞得我画面呈现全白的问题，一度认为Bezier曲面上的点出错，数值有误，仔细检查过方程式但有没什么问题呀， API。。。。
*         ⑤给定16个控制点 ，存放在三维数组中
*/#include <glut.h>
//存放16个控制点4*4
//双三次Bezier曲面指的是由两个二维Bezier曲线组成的二维曲面，
//每个Bezier曲线包含四个控制点，因此曲面上总共有16个控制点。 
float R[4][4][3] = {{{ -0.8f, -0.7f, 0.2f }, { -0.3f, -0.6f, 0.2f }, { 0.2f, -0.65f, 0.3f }, { 0.7f, -0.7f, 0.2f }},{{ -0.9f, -0.2f, 0.3f }, { -0.4f, -0.2f, 0.2f }, { 0.3f, -0.2f, 0.4f },    { 0.75f, -0.2f, 0.3f },},{{ -0.9f, 0.3f, 0.3f }, { -0.3f, 0.2f, 0.5f }, { 0.25f, 0.25f, 0.6f },    { 0.8f, 0.3f, 0.4f },},{{ -0.8f, 0.8f, 0.1f }, { -0.3f, 0.8f, 0.2f }, { 0.2f, 0.85f, 0.1f },    { 0.7f, 0.8f, 0.1f },}
};
//float uv[][3] = {0};//存放面上的点  [][][3]void display(void)
{glClear(GL_COLOR_BUFFER_BIT);//旋转 //glRotatef(-65.0, 1.0, 0.3, 0.2);/* glBegin(GL_LINE_STRIP);for (float v = 0; v <= 1; v += 0.01) {float B0v = (1 - v) * (1 - v) * (1 - v);float B1v = 3 * (1 - v) * (1 - v) * v;float B2v = 3 * (1 - v) * v * v;float B3v = v * v * v;for (float u = 0; u <= 1; u += 0.01) {float B0u = (1 - u) * (1 - u) * (1 - u);float B1u = 3 * (1 - u) * (1 - u) * u;float B2u = 3 * (1 - u) * u * u;float B3u = u * u * u;for (int j = 0; j < 4; j++) {uv[j][0] = R[0][j][0] * B0u + R[1][j][0] * B1u + R[2][j][0] * B2u + R[3][j][0] * B3u;uv[j][1] = R[0][j][1] * B0u + R[1][j][1] * B1u + R[2][j][1] * B2u + R[3][j][1] * B3u;uv[j][2] = R[0][j][2] * B0u + R[1][j][2] * B1u + R[2][j][2] * B2u + R[3][j][2] * B3u;}}float vx = uv[0][0] * B0v + uv[1][0] * B1v + uv[2][0] * B2v + uv[3][0] * B3v;float vy = uv[0][1] * B0v + uv[1][1] * B1v + uv[2][1] * B2v + uv[3][1] * B3v;float vz = uv[0][2] * B0v + uv[1][2] * B1v + uv[2][2] * B2v + uv[3][2] * B3v;glVertex3f(vx/100, vy/100, vz/100);}*///曲面分为u v方向 看作  错误理解为x-y轴//先计算一个u方向上的Bezier曲线上的点，存储在一个数组中  // 目标先求出有n行的曲线点数组// 曲线上的点有 xyz坐标值 有0-t行4列 ---> 三维数组 points_u[t][4][3]//该遍历有4列，每行四个控制点// //t相当于 在u从0到1.0变化时候存在的点数 u每次+0.01//上面被注释的代码没有 考虑到 二维怎么存放三维的问题 除非使用结构体？？？    /*for (float u = 0; u <= 1; u += 0.1) {float B0u = (1 - u) * (1 - u) * (1 - u);float B1u = 3 * (1 - u) * (1 - u) * u;float B2u = 3 * (1 - u) * u * u;float B3u = u * u * u;int t = 0;for (int j = 0; j < 4; j++) {points_u[t][j][0] = R[0][j][0] * B0u + R[1][j][0] * B1u + R[2][j][0] * B2u + R[3][j][0] * B3u;points_u[t][j][1] = R[0][j][1] * B0u + R[1][j][1] * B1u + R[2][j][1] * B2u + R[3][j][1] * B3u;points_u[t][j][2] = R[0][j][2] * B0u + R[1][j][2] * B1u + R[2][j][2] * B2u + R[3][j][2] * B3u;}t += 1;}*///此步同上面的步骤//已经计算出4行Bezier曲线上的点 ，接下来在这基础上在才求出（列）v方向的点//结合v方向（列）的控制点 即从控制点出发 慢慢地利用第一步计算出的Bezier曲线的点再得出Bezier曲线////设置一个存储最终Bezier曲面的点 //float points_uv[11][11][3] = { 0 };/*for (float v = 0; v <= 1; v += 0.1) {float B0v = (1 - v) * (1 - v) * (1 - v);float B1v = 3 * (1 - v) * (1 - v) * v;float B2v = 3 * (1 - v) * v * v;float B3v = v * v * v;int t = 0;for (int j = 0; j < 11; j++) {points_uv[j][t][0] = points_u[j][0][0] * B0v + points_u[j][1][0] * B1v + points_u[j][2][0] * B2v + points_u[j][3][0] * B3v;points_uv[j][t][0] = points_u[j][0][1] * B0v + points_u[j][1][1] * B1v + points_u[j][2][1] * B2v + points_u[j][3][1] * B3v;points_uv[j][t][0] = points_u[j][0][2] * B0v + points_u[j][1][2] * B1v + points_u[j][2][2] * B2v + points_u[j][3][2] * B3v;}t += 1;}*///设置11是因为  t每次增加0.1  到1.0就有11个 //数组定义为 point_u[11][4][3]  选取垂直方向 每4个垂直的（看作近似在一条线）控制点组成Bezier曲线 可以算出行//也可以定义为point_u[4][11][3] 但后面要改变方向为R[j][0][0]   //这里直接跟着这条式子思考 ux[j] = RX[0][j]*B0u + RX[1][j]*B1u + RX[2][j]*B2u + RX[3][j]*B3u;  也是选取竖直方向  //也可选水平方向float points_u[11][4][3] = { 0.0 };for (int j = 0; j < 4; j++) {int t = 0;for (double u = 0.0; u <= 1.0; u += 0.1){float B0u = (1 - u) * (1 - u) * (1 - u);float B1u = 3 * (1 - u) * (1 - u) * u;float B2u = 3 * (1 - u) * u * u;float B3u = u * u * u;points_u[t][j][0] = R[0][j][0] * B0u + R[1][j][0] * B1u + R[2][j][0] * B2u + R[3][j][0] * B3u;points_u[t][j][1] = R[0][j][1] * B0u + R[1][j][1] * B1u + R[2][j][1] * B2u + R[3][j][1] * B3u;points_u[t][j][2] = R[0][j][2] * B0u + R[1][j][2] * B1u + R[2][j][2] * B2u + R[3][j][2] * B3u;t = t + 1;}}// 行列 11*11float points_uv[11][11][3] = { 0.0 };for (int j = 0; j < 11; j++) {int i = 0;for (double t = 0.0; t <= 1.0; t += 0.1){float a1 = (1 - t) * (1 - t) * (1 - t);float a2 = 3 * (1 - t) * (1 - t) * t;float a3 = 3 * t * t * (1 - t);float a4 = t * t * t;points_uv[j][i][0] = a1 * points_u[j][0][0] + a2 * points_u[j][1][0] + a3 * points_u[j][2][0] + a4 * points_u[j][3][0];points_uv[j][i][1] = a1 * points_u[j][0][1] + a2 * points_u[j][1][1] + a3 * points_u[j][2][1] + a4 * points_u[j][3][1];points_uv[j][i][2] = a1 * points_u[j][0][2] + a2 * points_u[j][1][2] + a3 * points_u[j][2][2] + a4 * points_u[j][3][2];i = i + 1;}}//Bezier曲面上的点连线glColor3f(1.0, 0.0, 1.0);for (int i = 0; i < 11; i++) {glBegin(GL_LINE_STRIP);for (int j = 0; j < 11; j++)glVertex3fv(&points_uv[i][j][0]);glEnd();glBegin(GL_LINE_STRIP);for (int j = 0; j < 11; j++)glVertex3fv(&points_uv[j][i][0]);glEnd();}//绘画控制点    glPointSize(10.0);glColor3f(1.0, 0.0, 0.0);for (int i = 0; i < 4; i++) {glBegin(GL_POINTS);for (int j = 0; j < 4; j++)glVertex3fv(&R[i][j][0]);glEnd();}//绘画连接控制点的连线glColor3f(1.0, 1.0, 1.0);for (int i = 0; i < 4; i++) {glBegin(GL_LINE_STRIP);for (int j = 0; j < 4; j++)glVertex3fv(&R[i][j][0]);glEnd();glBegin(GL_LINE_STRIP);for (int j = 0; j < 4; j++)glVertex3fv(&R[j][i][0]);glEnd();}//glFlush();glutSwapBuffers();
}int main(int argc, char** argv)
{glutInit(&argc, argv);//glutInitDisplayMode(GLUT_RGBA | GLUT_SINGLE);glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE);glutInitWindowPosition(200, 200);glutInitWindowSize(600, 600);glutCreateWindow("Bezier Surface");glutDisplayFunc(display);glutMainLoop();return 0;
}

GitHub:https://github.com/twj1206/homework/tree/main/Bicubic%20Bezier%20surface/test

参考：https://blog.csdn.net/lafengxiaoyu/article/details/51295464

这篇关于双三次Bezier曲面的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/304204。

相关文章

图解TCP三次握手｜深度解析｜为什么是三次

图解TCP三次握手｜深度解析｜为什么是三次

写在前面 这篇文章我们来讲解析 TCP三次握手。 TCP 报文段 传输控制块TCB：存储了每一个连接中的一些重要信息。比如TCP连接表，指向发送和接收缓冲的指针，指向重传队列的指针，当前的发送和接收序列等等。 我们再来看一下TCP报文段的组成结构 TCP 三次握手 过程 假设有一台客户端，B有一台服务器。最初两端的TCP进程都是处于CLOSED关闭状态，客户端A打开链接，服务器端
阅读更多...
TCP三次握手详解！

TCP三次握手详解！

TCP(Transmission Control Protocol)　传输控制协议 三次握手 TCP是主机对主机层的传输控制协议，提供可靠的连接服务，采用三次握手确认建立一个连接: 位码即tcp标志位,有6种标示:SYN(synchronous建立联机) ACK(acknowledgement 确认) PSH(push传送) FIN(finish结束) RST(reset重置) UR
阅读更多...
Linux - Tcp连接建立和释放的三次握手四次挥手

Linux - Tcp连接建立和释放的三次握手四次挥手

一、TCP报文段首部格式         源端口/目的端口：各占2个字节，分别写入源端口和目的端口，端口是传输层与应用层的服务接口    序号：占4个字节，TCP连接中传送的数据流中每一个字节都有一个序号，序号字段指本报文段所发送的数据的第一个字节的序号    确认号：占4个字节，是期望收到对方下一个报文的第一个数据字节的序号    数据偏移：占4个字节，它指出TCP报文的数据距离TCP
阅读更多...
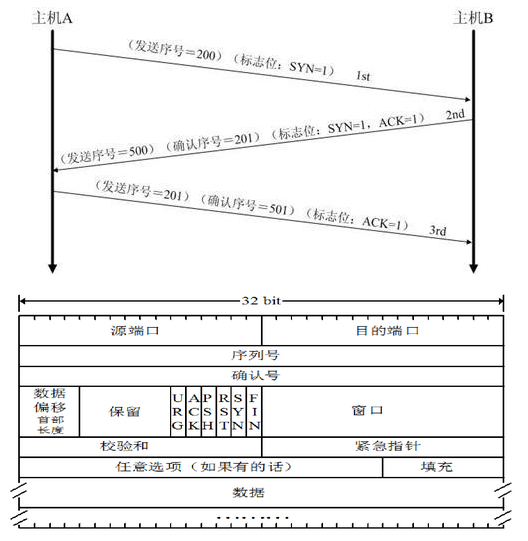
tcp三次握手及其必要性

tcp三次握手及其必要性

TCP/IP协议中，TCP协议提供可靠的连接服务，采用三次握手建立一个连接，如下图所示。 主机A为客户机，主机B为服务器 确认号：其数值等于发送方的发送序号 +1(即接收方期望接收的下一个序列号)。 说明： （1）第一次握手：建立连接时，客户端A发送SYN包（SYN=j）到服务器B，并进入SYN_SEND状态，等待服务器B确认。 （2）第二次握手：服务器B收到SY
阅读更多...
nurbs曲面和贝塞尔曲面的区别是什么

nurbs曲面和贝塞尔曲面的区别是什么

NURBS曲面和贝塞尔曲面的主要区别如下：   定义与理论基础：   NURBS曲面：全称非均匀有理B样条曲面，是NURBS曲线在二维空间上的扩展。它结合了非均匀性、有理性和B样条的特性，能够更灵活地表示复杂曲面。 贝塞尔曲面：通过Bernstein基函数的张量积为加权系数对控制顶点进行线性组合所构造的参数曲面。它具有良好的连续性和插值性质。   控制点的灵活性与局部性：   N
阅读更多...
[Linux网络]TCP三次握手和四次挥手的连接建立和断开

[Linux网络]TCP三次握手和四次挥手的连接建立和断开

TCP的三次握手 第一次握手：客户端发送网络包，服务器端收到，证明客户端的发送能力、服务器的接收能力是正常的。第二次握手：服务器发送网络包，客户端收到，证明服务器端的发送能力是正常的，不过此时并不能确定，客户端的接收能力是正常的。第三次握手：客户端发包，服务器端收到，服务器端可以得出结论，客户端的发送，接收能力是正常的。服务器端的接收，发送能力是正常的。 什么是半连接队列？ 服务器端第一次
阅读更多...
Nginx: 性能优化之提升CPU效率以及TCP的三次握手和四次挥手

Nginx: 性能优化之提升CPU效率以及TCP的三次握手和四次挥手

提升利用CPU的效率 1 ）CPU的调度机制 现在来看下 linux中 CPU的一个调度机制 假设现在系统上有只有一颗CPU，而linux系统是一个多任务的一个操作系统 它允许我们各个不同的用户允许在同一个操作系统上执行很多个进程 单核CPU肯定不可能同时去执行这样一些程序 CPU在同一时刻只能够调度一个进程来执行，没办法并发执行多个程序 从宏观上来看，多任务系统，都是能够一起
阅读更多...
TCP 之 三次握手 (面经计网篇)

TCP 之 三次握手 (面经计网篇)

这是tcp 简历连接的三次握手方式 , 其中的特殊符号 , 我解释下 , SYN 是 同步的这个单词(synchronization), ACK 是回执,承认的单词(acknowledgement), SYN-ACK 服务器收到SYN报文后，回复一个带有SYN和ACK标志的报文段，这表示服务器已经收到了客户端的SYN报文，并且期望收到下一个字节的序列号为服务器传递的确认号。拓展1,2,3 （介
阅读更多...
fpga图像处理实战-双三次插值算法

fpga图像处理实战-双三次插值算法

双三次插值算法         双三次插值（Bicubic Interpolation）是一种常用的图像处理算法，用于在图像缩放、旋转等操作中进行像素的插值。相比于简单的双线性插值，双三次插值能提供更高的图像质量，尤其是在放大图像时，可以更好地保留细节。 基本原理         双三次插值通过考虑周围16个像素点（一个4x4的邻域）的灰度值来计算插值点的值。其核心思想是利用三次多项式进行插
阅读更多...
【传输层协议】TCP协议(上) {TCP协议段格式；确认应答机制；超时重传机制；连接管理机制：三次握手、四次挥手}

【传输层协议】TCP协议(上) {TCP协议段格式；确认应答机制；超时重传机制；连接管理机制：三次握手、四次挥手}

TCP（Transmission Control Protocol）是一种面向连接的、可靠的、基于字节流的传输层协议，用于在网络上可靠地传输数据。TCP是互联网协议套件（TCP/IP）中的一个主要协议，它在IP（Internet Protocol）的基础之上提供了可靠的数据传输服务。 TCP协议具有以下特点和功能： 面向连接：在通信双方进行数据传输之前，需要建立TCP连接，包括三次握手和四次
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2