曲面专题
nurbs曲面和贝塞尔曲面的区别是什么
NURBS曲面和贝塞尔曲面的主要区别如下： 定义与理论基础： NURBS曲面：全称非均匀有理B样条曲面，是NURBS曲线在二维空间上的扩展。它结合了非均匀性、有理性和B样条的特性，能够更灵活地表示复杂曲面。 贝塞尔曲面：通过Bernstein基函数的张量积为加权系数对控制顶点进行线性组合所构造的参数曲面。它具有良好的连续性和插值性质。 控制点的灵活性与局部性： N
UG NX二次开发(C++)-获取曲面的相切曲面
文章目录 1、前言2、创建一个三维模型3、获取相切曲面的方法3、测试结果 1、前言 最近一段时间，QQ群中的群友总问我一个问题，那就是如何获取曲面的相切曲面，我今天就把这个方法写出来，以帮助读者。 在UG二次开发中，查询了帮助文档，没有找到获取相切曲面的函数。所以采用NXOpen来获取。如果有关于UG NX二次的疑问或者想学习UG NX二次开发技术，可以私信博主。 2、创建
【流体力学】第二章 流体静力学,流体静压强及其特性，静止流体内压强分布，作用在平面和曲面上的流体压力（西北工业大学）
目录 第二章 流体静力学 2.1 流体静压强及其特性 一、基本概念 1.静压强 二、静压强的特性 2.2 静止流体平衡微分方程式编辑 二、 平衡微分方程的积分 三、 等压面 2.3 重力场中静止流体内的压强分布 三. 位置水头、压强水头、测压管水头 四. 压强的度量单位 2.4 压强测量 一. 绝对压强、相对压强、真空 二. 测压原理 U形测压管
B样条曲线曲面--拟合技术
B样条曲线曲面 1.B样条曲线 B样条曲线（B-spline curve）是一种在计算机图形学和计算几何中广泛使用的参数曲线。它是贝塞尔曲线（Bezier curve）的一种推广，提供了更好的局部控制能力。B样条曲线由一组控制点（也称为控制顶点）和一组基函数（称为B样条基函数）定义。 1.1.B样条曲线的定义 给定一组 ( n + 1 ) 个控制点 ( P i ) 和一组节点（ k n
Bezier曲线曲面--拟合技术
Bezier曲线曲面–拟合应用 1.Bezier曲线 1.1.Bezier曲线的定义 给定一组控制点 P_0, P_1, …, P_n，其中 n 是曲线的阶数，Bezier曲线的参数方程可以表示为： B ( t ) = ∑ i = 0 n P i b i , n ( t ) , t ∈ [ 0 , 1 ] B(t) = \sum_{i=0}^{n} P_i b_{i,n}(t), \qua
有理B样条曲线曲面（NURBS）--拟合技术
非有理B样条曲线曲面（NURBS） 1.NURBS曲线 NURBS（Non-Uniform Rational B-Spline）曲线是一种在计算机辅助设计（CAD）和计算机图形学中广泛使用的数学表示方法，用于精确地定义和渲染复杂的曲线和曲面。NURBS曲线结合了B-Spline曲线和Bezier曲线的优点，提供了对曲线形状的精确控制以及对曲线几何和拓扑属性的灵活操作。 1.1.NURBS曲线
计算机图形学入门18：曲面
1.曲面定义 曲面（Surface）在图形学中应用非常广泛，可以用它来描述各种三维物体的表面。如下图所示。 2.贝塞尔曲面 2.1 介绍 曲线和曲面一样都是物体显示的表示方法，自然可以把曲线的概念延伸到平面上。如上图所示，就是贝塞尔曲面(Bezier Surface)构成的表面，并且可以看到是分段面拼接的。 如果对完整的表面进行分解
Matlab进阶绘图第60期—带伪彩图的曲面图
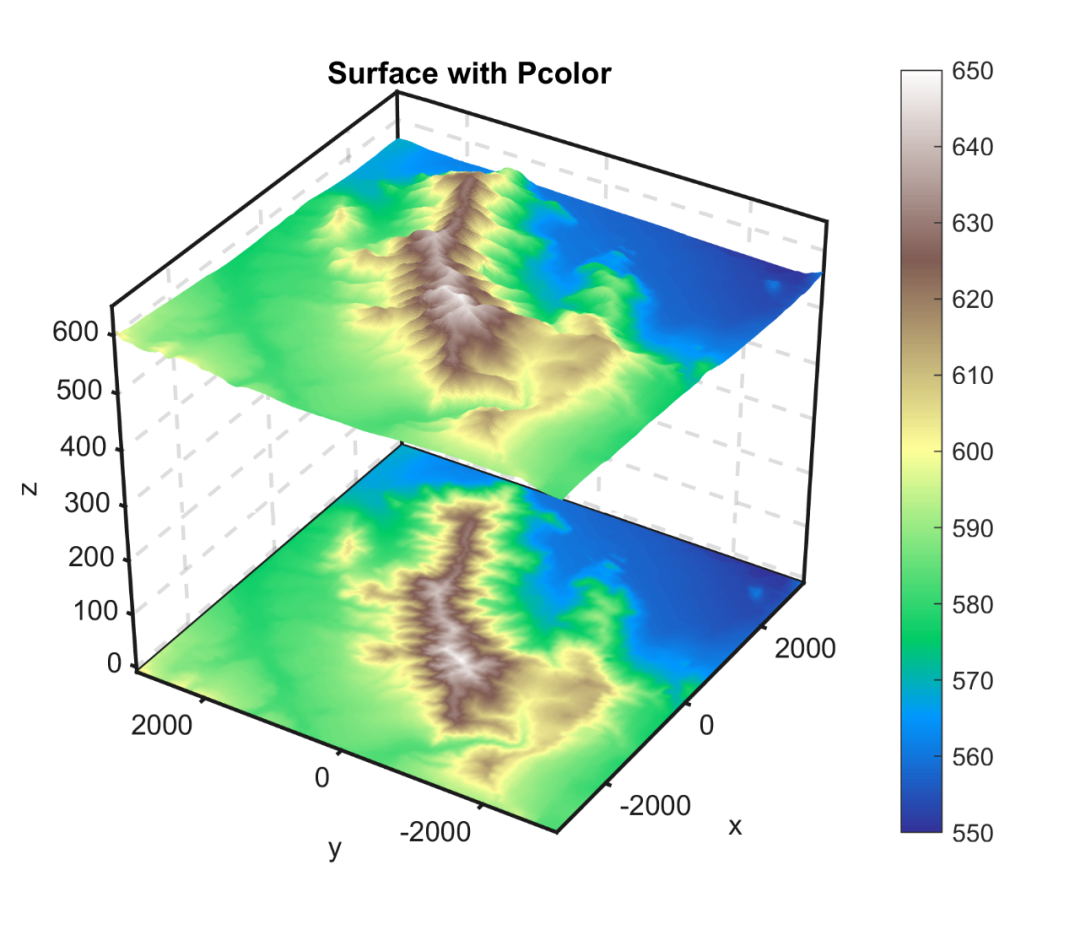
带伪彩图的曲面图是曲面图与伪彩图的组合。 其中，伪彩图与曲面图的颜色用于表示同一个特征。 由于伪彩图无遮挡但不直观，曲面图直观但有遮挡，而将二者组合，可以实现优势互补。 本期就来分享一下带伪彩图的曲面图的绘制方法，先来看一下成品效果： 特别提示：本期内容『数据+代码』已上传资源群中，加群的朋友请自行下载。有需要的朋友可以关注同名公号【阿昆的科研日常】，后台回复关键词【绘图桶】查看加
UG曲面刻字编程怎么做：深入解析与实操指南
UG曲面刻字编程怎么做：深入解析与实操指南 在UG（Unigraphics NX）这一强大的CAD/CAM/CAE一体化软件中，曲面刻字编程是一项既具挑战性又富有创造性的任务。本文将带您深入了解UG曲面刻字编程的全过程，从四个方面、五个方面、六个方面和七个方面为您详细解析，助您轻松掌握这一技能。 四个方面：理解刻字需求与曲面特性 在进行UG曲面刻字编程前，首先需要明确刻字的具体需求，包括字体
Civil 3d中 三角网曲面求取二维和三维面积
直接来点源码： public void CreateTinSurfaceArea() { try { string strErr = ""; ObjectId sId = PromptOptionsHelper.GetPromptEntOptions("请选择曲面",
Maya: 菜单 编辑NURBS 重建曲面
编辑NURBS >重建曲面 这是一个经常使用到的命令，在利用”放样”等命令使曲线生成曲面时，容易造成曲面上的曲线分布不均的现象，这时就可以使用该命令来重新分布曲面的UV方向。
Maya: 菜单 细分曲面 部分折痕边/顶点
细分曲面 >部分折痕边/顶点 在细分曲面模型元素编辑模式下，选择接近折痕的边或点后执行“部分折痕边/顶点”命令，在折痕处产生的倒角不会出现生硬效果，也不会在折痕处形成硬边。
由两个曲面确定的交线的切向量求解
由两个曲面确定的交线的切向量求解 @(微积分) 有一个很有启发性的说法：考虑描述曲面的隐函数 F(x,y,z)=0. F(x,y,z)=0. 其全微分 dF=F′xdx+F′ydy+F′zdz=0 dF=F'_xdx+F'_ydy+F'_zdz=0,即 (F′x,F′y,F′z)(dx,dy,dz)=0 (F'_x,F'_y,F'_z)(dx,dy,dz) = 0 其中， (dx,dy
关于第一型曲面积分的再思考
关于第一型曲面积分的再思考 @(微积分) 有些问题，看着复杂，却很好解。同样，有些问题看着很简单，但是却很难下手。举一个关于第一型曲面积分计算的例子。 第一型曲面积分基础解法要干三件事： 投影代入计算 三件事之间没有逻辑顺序，想先干谁就干谁。 目标是为了化为二重积分。曲面太弯了，我们需要在比较直的场面下才好进行积分。 或者可以固化为一种自己喜欢的顺序： 一投二代三计算 设曲
CATIA进阶操作——创成式曲面设计入门（1）线架设计，三维点、直线、平面、曲线
目录 引出三维空间点生成三维直线三维平面三维曲线总结异形弹簧新建几何体草图编辑，画一条样条线进行扫掠，圆心和半径画出曲面上的螺旋线再次选择扫掠，圆心和半径 其他自定义信号和槽1.自定义信号2.自定义槽3.建立连接4.进行触发 自定义信号重载带参数的按钮触发信号触发信号拓展 lambda表达式返回值mutable修饰案例 引出 CATIA进阶操作——创成式曲面设计入门（1）
曲面细分技术在AI去衣中的创新应用
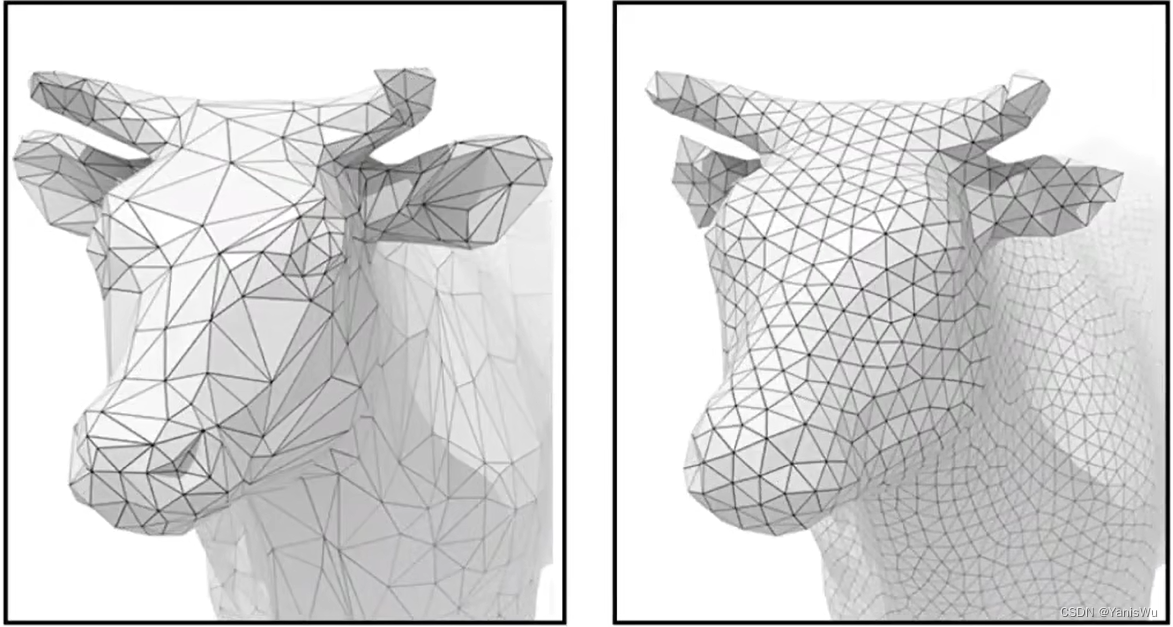
引言： 随着人工智能技术的飞速发展，其在图像处理领域的应用日益广泛。其中，AI去衣技术因其独特的应用场景而备受瞩目。在这一技术的发展过程中，曲面细分技术发挥了至关重要的作用。本文将深入探讨曲面细分技术在AI去衣中的作用及其背后的原理。 一、曲面细分技术概述 曲面细分技术是一种高效的多边形网格生成方法，它通过递归地分割现有的多边形网格来生成更精细的网格。这种技术可以用于创建复杂的三维模型，同时也
【Matlab函数分析】绘图函数：mesh网格曲面图
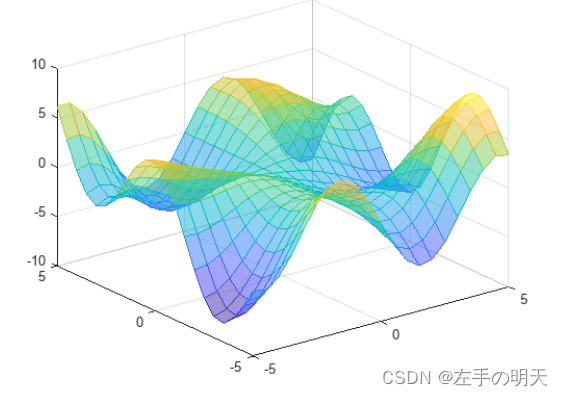
🔗 运行环境：Matlab 🚩 撰写作者：左手の明天 🥇 精选专栏：《python》 🔥 推荐专栏：《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好🤗🤗🤗，我是左手の明天！好久不见💗 💗今天更新系列【Matlab函数分析】——mesh网格曲面图💗 📆 最近更新：2024 年 05 月 29 日，左手の明天的第 334 篇原创博客 📚 更新
超全的matlab绘图实例及代码(曲线，曲面，饼状图，柱形图，网格图，球面等)
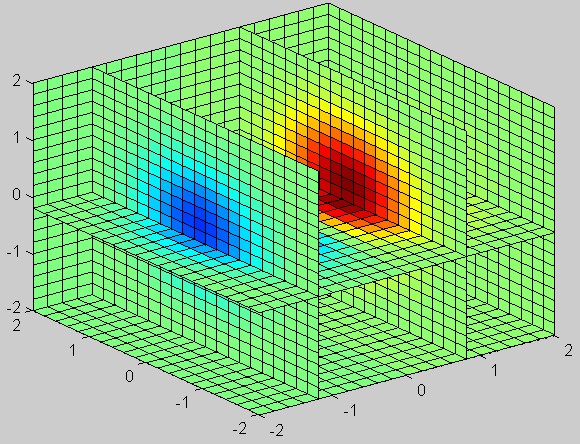
1、三维曲线 >> t=0:pi/50:10*pi; >> plot3(sin(2*t),cos(2*t),t) >> axis square >> grid on 2、一窗口多图形 >> t=-2*pi:0.01:2*pi; >> subplot(3,2,1) >> plot(t,sin(t)) >> subplot(3,2,2) >> plot(t,cos(t)) >> subplot(3
Python绘制3D曲面图
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 探索Python中绘制3D曲面图的艺术 在数据可视化的世界中，3D曲面图是一种强大的工具，能够将复杂的数据模式以清晰直观的方式展现出来。Python提供了多种库和工具，使得创建和定制3D曲面图变得简单而令人兴奋。本文将介绍如何使用Python中的Matp
Tessellation Shader（细分曲面着色器）
Tessellation Shader）是OpenGLES4.0引入的，处于顶点着色器阶段的下一个阶段，它是由ATI在2001年率先设计出来的。 细分曲面着色器 直到这个阶段，对于操作几何图元而言，只有顶点着色器对我们可用。尽管使用顶点着色器可以使用不少图形技术，不过顶点着色器也确实存在一些限制。一个就是它们在执行过程中无法创建额外的几何图形。它们仅仅更新与它们当前所处理的顶点相关的数
《MATLAB科研绘图与学术图表绘制从入门到精通》示例：绘制伊甸火山3D网格曲面图
11.4.2小节我们使用3D曲面图可视化分析伊甸火山数据，本小节我们采用3D网格曲面图可视化分析伊甸火山数据，以展示其地形，具体示例代码如下。 购书地址：https://item.jd.com/14102657.html