超全的matlab绘图实例及代码(曲线，曲面，饼状图，柱形图，网格图，球面等)

本文主要是介绍超全的matlab绘图实例及代码(曲线，曲面，饼状图，柱形图，网格图，球面等)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

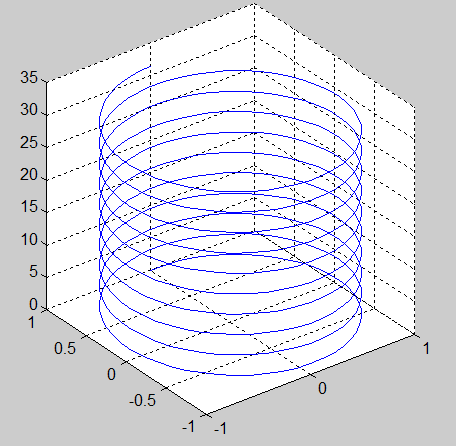
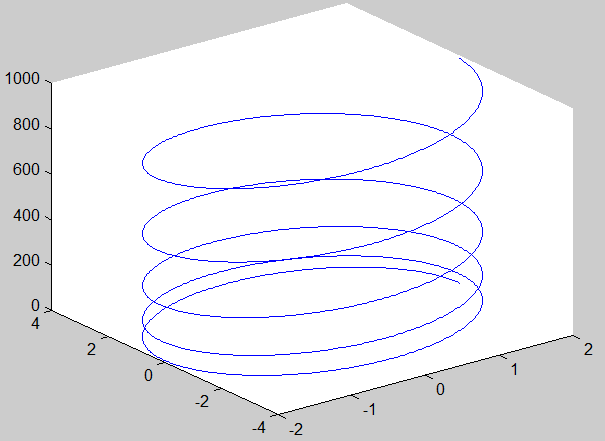
1、三维曲线
>> t=0:pi/50:10*pi;
>> plot3(sin(2*t),cos(2*t),t)
>> axis square
>> grid on

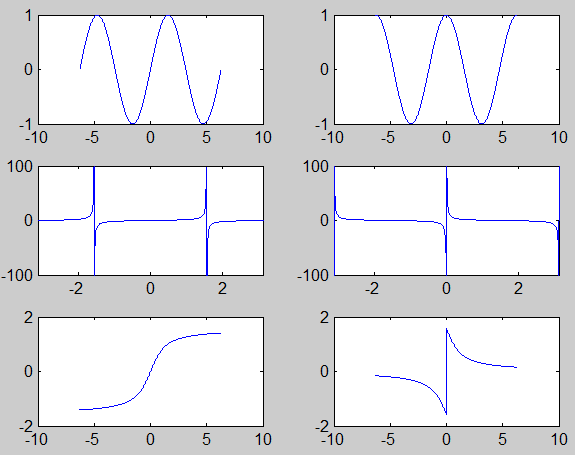
2、一窗口多图形
>> t=-2*pi:0.01:2*pi;
>> subplot(3,2,1)
>> plot(t,sin(t))
>> subplot(3,2,2)
>> plot(t,cos(t))
>> subplot(3,2,3)
>> plot(t,tan(t))
>> axis([-pi pi -100 100])
>> subplot(3,2,4)
>> plot(t,cot(t))
>> axis([-pi pi -100 100])
>> subplot(3,2,5)
>> plot(t,atan(t))
>> subplot(3,2,6)
>> plot(t,acot(t))

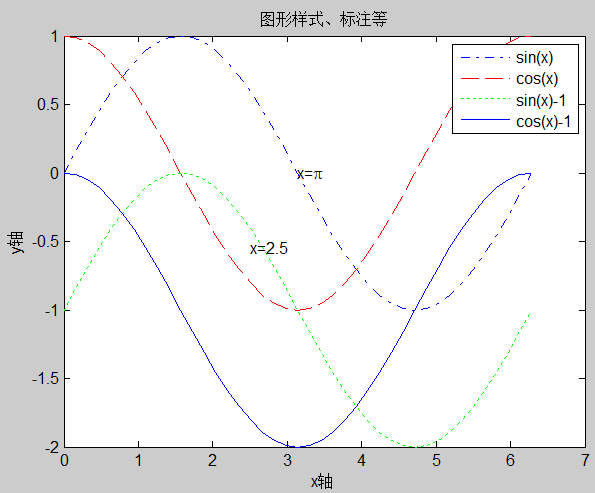
3、图形样式、标注、题字
(也可以利用菜单直接Insert)
>> x=0:pi/20:2*pi;
>> plot(x,sin(x),'b-.')
>> hold on
>> plot(x,cos(x),'r--')
>> hold on
>> plot(x,sin(x)-1,'g:')
>> hold on
>> plot(x,cos(x)-1)
>> xlabel('x');
>> xlabel('x轴');
>> ylabel('y轴');
>> title('图形样式、标注等');
>> text(pi,sin(pi),'x=\pi');
>> legend('sin(x)','cos(x)','sin(x)-1','cos(x)-1');
>> [x1,y1]=ginput(1) %利用鼠标定位查找线上某点的值
x1 =
2.0893
y1 =
-0.5000
>> gtext('x=2.5') %鼠标定位放置所需的值在线上

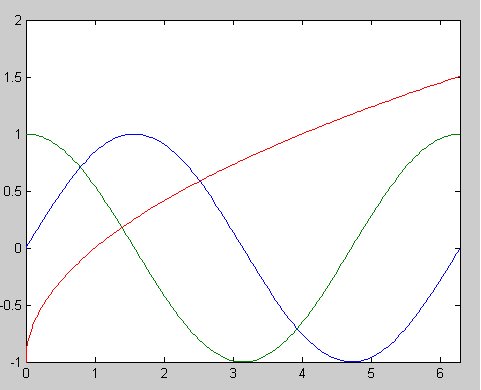
4、
>> fplot('[sin(x),cos(x),sqrt(x)-1]',[0 2*pi])

M文件：myfun.m
内容如下：
function y=myfun(x)
y(:,1)=sin(x);
y(:,2)=cos(x);
y(:,3)=x^(1/2)-1;
再运行：>> fplot('myfun',[0 2*pi])
同样可以得到右图

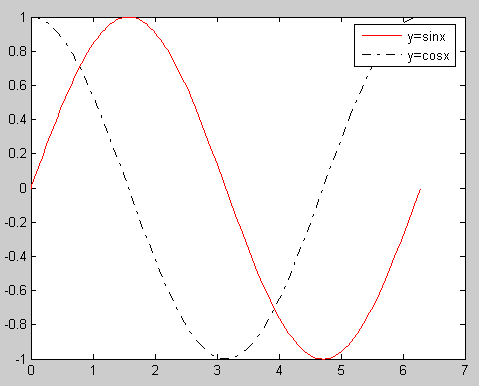
5、
>> [x,y]=fplot('sin',[0 2*pi]);
>> [x1,y1]=fplot('cos',[0 2*pi]);
>> plot(x,y,'-r',x1,y1,'-.k')
>> legend('y=sinx','y=cosx')

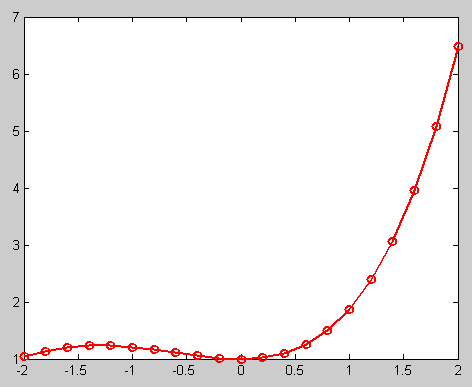
6、
>> x=[-2:0.2:2];
>> y=exp(x)-sin(x);
>> plot(x,y,'-or','linewidth',2)

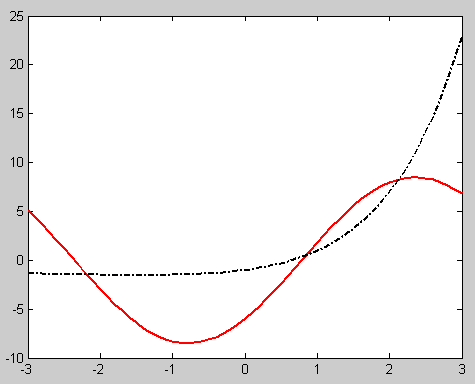
7、画出y1=6(sinx-cosx),y2=x2^x-1的图形
>> x=[-3:0.1:3];
>> y1=6*(sin(x)-cos(x));
>> y2=x.*2.^x-1;
>> plot(x,y1,'-r',x,y2,'-.k','linewidth',2)

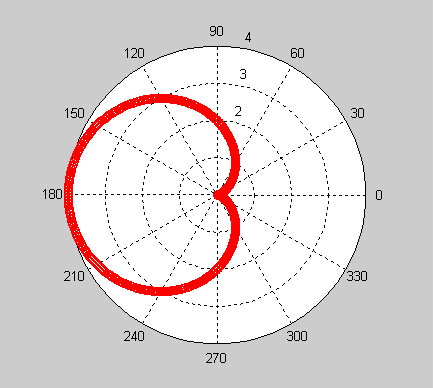
8、绘制心形图r=2(1-cos )的极坐标图形
>> theta=[0:0.01:2*pi];
>> polar(theta,2*(1-cos(theta)),'-k')
>> polar(theta,2*(1-cos(theta)),'-or')

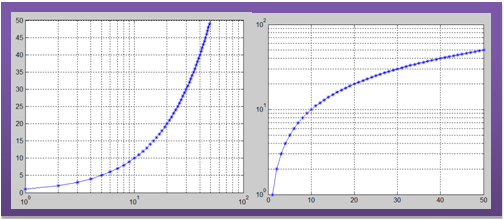
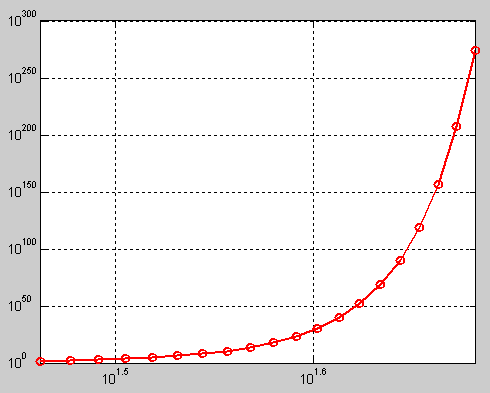
9、用双轴对数坐标绘制y=x*3^x-30的图形
>> x=logspace(-3,3);
>> y=x.*3.^x-30;
>> loglog(y,'-or','linewidth',2);
>> grid on

10、绘制数据向量的单轴对数坐标图形
>> x=[1:50];
>> y=[1:50];
>> semilogx(x,y,'-*b')
%绘制横轴为对数坐标
%纵轴为线性坐标
>> grid on
>> semilogy(x,y,'-*b')
%绘制纵轴为对数坐标
%横轴为线性坐标
>> grid on

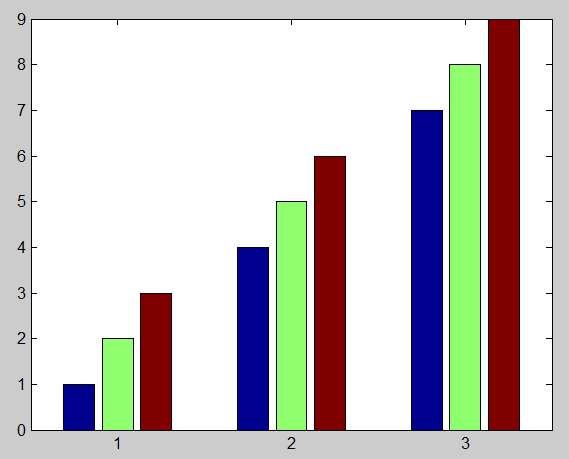
11、绘制矩阵A=((1,2,3),(4,5,6),(7,8,9))的条形图，
并求出句柄属性值向量。
>> A=[1 2 3;4 5 6;7 8 9];
>> h=bar(A)
h =
171.0031 174.0026 176.0026

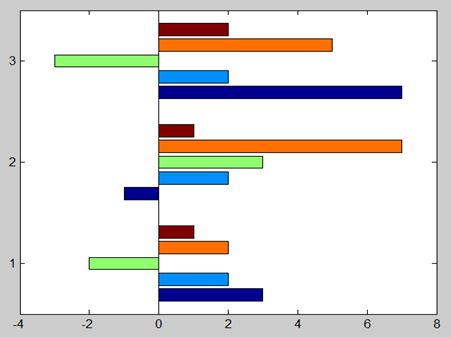
12、绘制矩阵的水平条形图。
>> y=[3 2 -2 2 1;-1 2 3 7 1;7 2 -3 5 2];
>> x=[1:3];
>> barh(x,y)

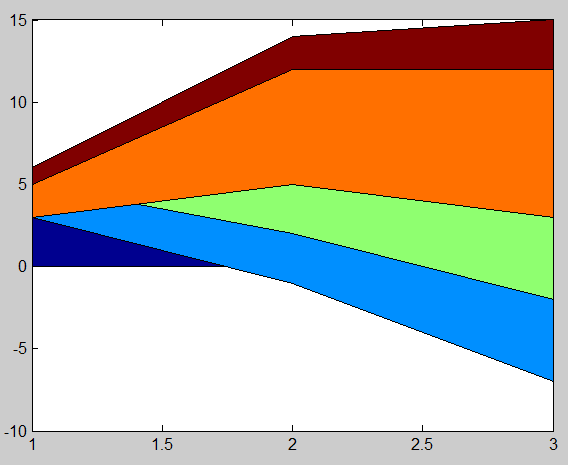
13、绘制矩阵的面积图。
>> y=[3 2 -2 2 1;-1 3 3 7 2;-7 5 5 9 3];
>> area(y)

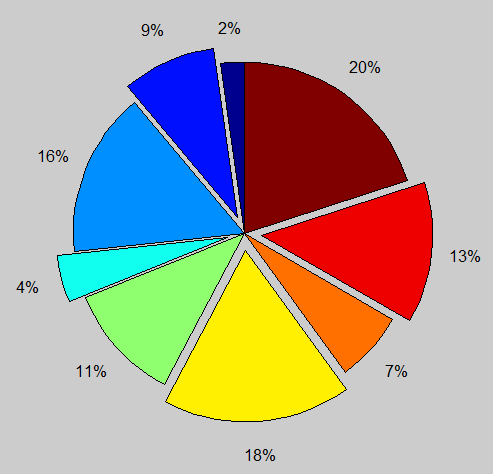
14、绘制矩阵的二维饼图
>> x=[1 2 3;4 5 6;7 8 9];
>> explode=[0 1 0 1 0 1 0 1 0];
>> pie(x,explode)

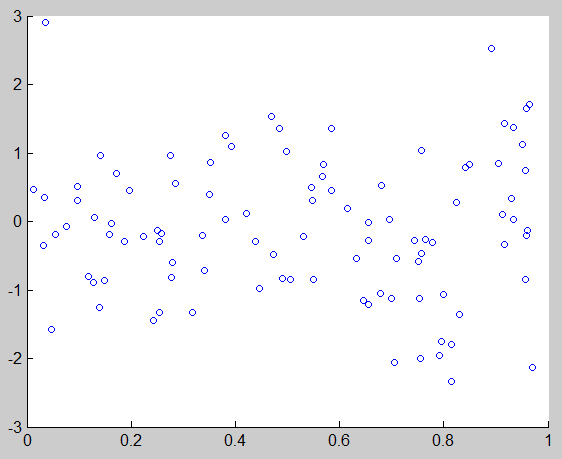
15、自行确定数据向量，绘制其散点图。
>> x=rand(1,100);y=randn(1,100);scatter(x,y,20)

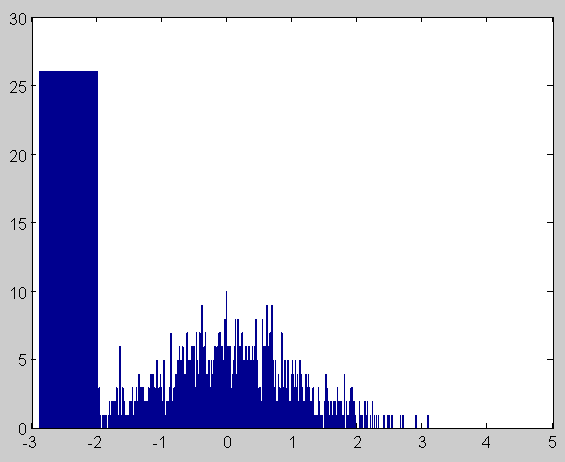
16、自行确定数据，绘制其柱形图。
>> x=[-2:0.01:4];
>>y=randn(1131,1);
>>hist(y,x)

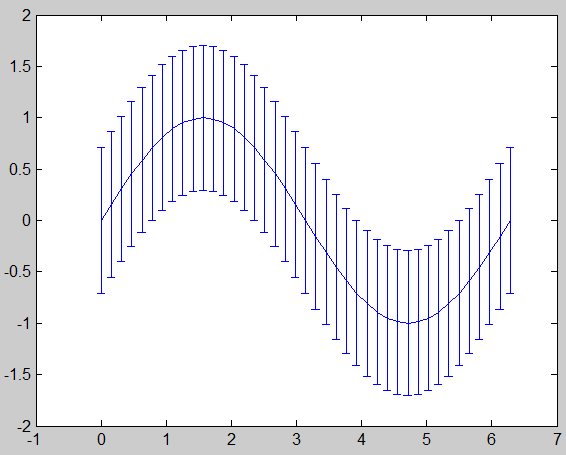
17、绘制y=sinx在[0,2*pi]
上的误差图。
>> x=[0:pi/20:2*pi];
>> y=sin(x);
>> E=std(y)*ones(size(x));
%条形控制
>> errorbar(x,y,E)

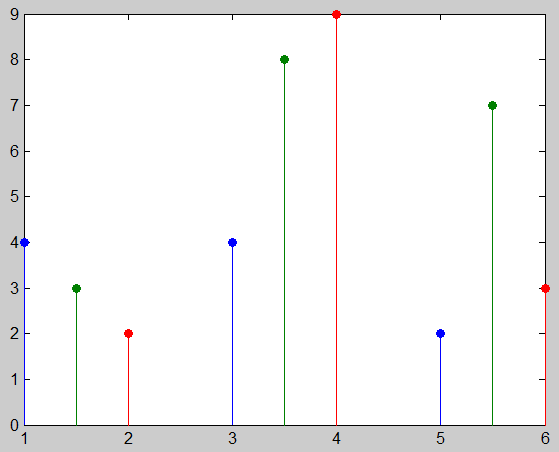
18、绘制火柴杆图。
>> x=[1 1.5 2;3 3.5 4;5 5.5 6];
>> y=[4 3 2;4 8 9;2 7 3];
>> stem(x,y,'fill')
%fill意思是“实心点”

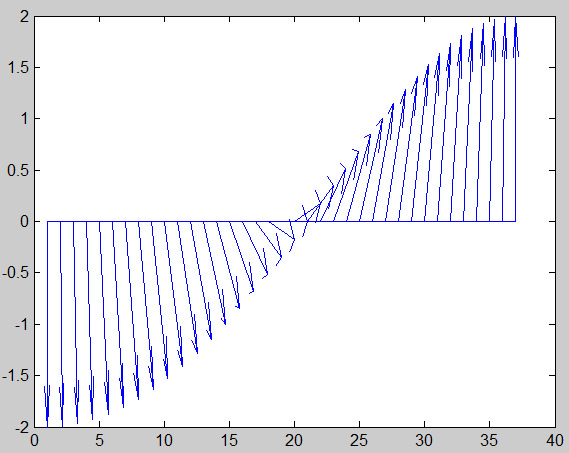
19、绘制羽列图。
>> U=[-90:5:90]*pi/180;
%建立等间距数据
>> V=2*ones(size(U));
%根据U建立数据
>> [U,V]=pol2cart(U,V);
转换数据为直角坐标形式
>> feather(U,V)

20、同一窗口绘制y=50e^(-x/20) sinx
和y= 1/2 e^(-x/2) cos⁡x在[0,30]上的图形。
>> x=[0:0.01:30];
>> y1=50*exp(-0.05*x).*sin(x);
>> y2=0.5*exp(-0.5*x).*cos(x);
>> plotyy(x,y1,x,y2,'plot')
% plotyy(x,y1,x,y2,'plot')表示：
用左侧y标度绘制（x,y1）
用右侧y标度绘制（x,y2）

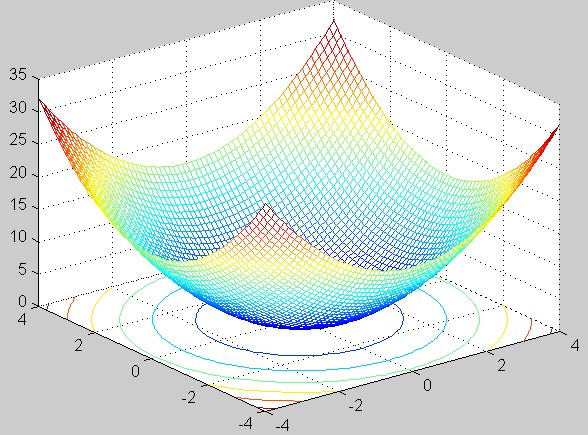
21、在-4<=x<=4,-4<=y<=4区域上

绘制z=x^2+y^2的三维网格图。

>> [x,y]=meshgrid(-4:0.125:4);

>> z=x.^2+y.^2;

>> meshc(x,y,z)

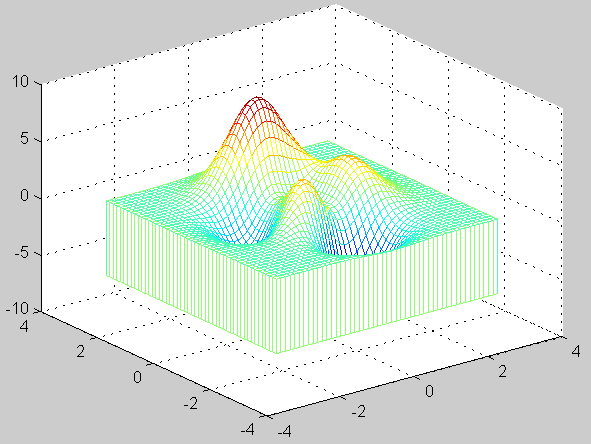
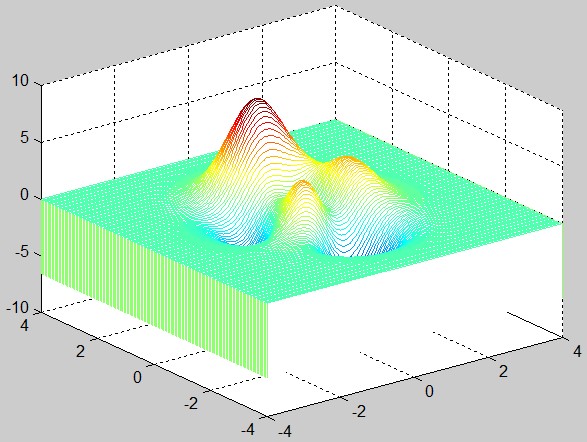
22、绘制高斯分布函数的网格图。
>> [x,y]=meshgrid(-3:0.125:3);
>> z=peaks(x,y);
>> meshz(x,y,z)

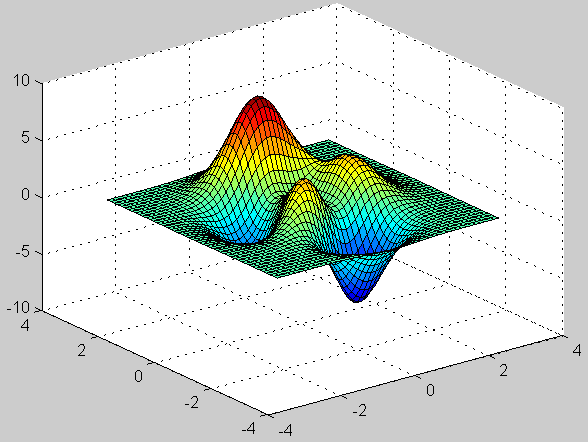
23、用surf绘制高斯分布函数的曲面图。
>> [x,y]=meshgrid(-3:0.125:3);
>>z=peaks(x,y);
>>surf(x,y,z)

24、绘制曲线图。
>> t=[0:pi/200:10*pi];
>> x=2*cos(t);
>> y=3*sin(t);
>> z=t.^2;
>> plot3(x,y,z)

25、利用peaks函数产生的数据绘制其带形图。
>> [x,y]=meshgrid([-2*pi:pi/5:2*pi],[-2:1/5:2]);
>> z=peaks(x,y);
>> ribbon(y,z)

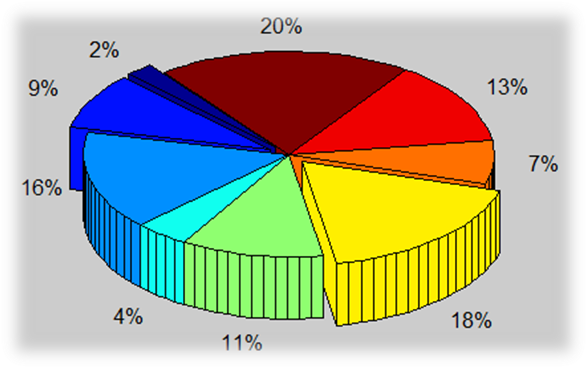
26、绘制三维饼图。
>> A=[1 2 3;4 5 6;7 8 9];
>> ex=[1 0 0;4 0 0;0 8 0];
>> pie3(A,ex)

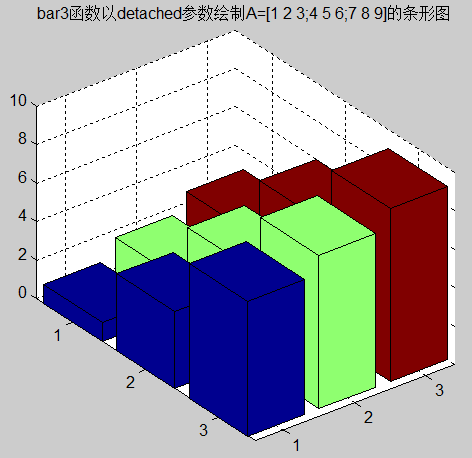
27、在各种style参数的条件下绘制矩阵的三维条形图。
>> z=[1 2 3;4 5 6;7 8 9];
>>bar3(z,'detached')
>>title('bar3函数以detached参数绘制A=[1 2 3;4 5 6;7 8 9]的条形图')
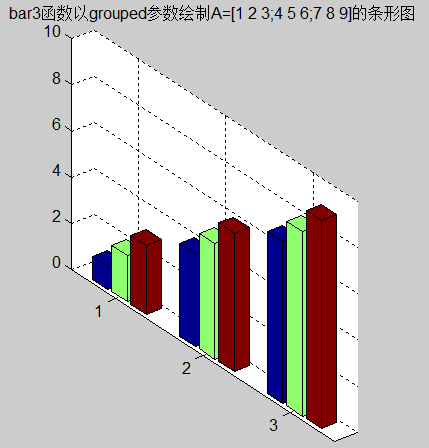
>> bar3(z,'grouped')
>> title('bar3函数以grouped参数绘制A=[1 2 3;4 5 6;7 8 9]的条形图')
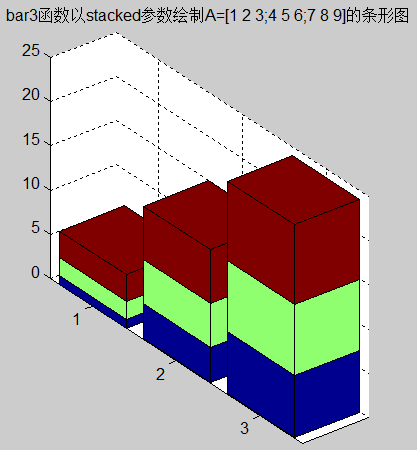
>> bar3(z,'stacked')
>> title('bar3函数以stacked参数绘制A=[1 2 3;4 5 6;7 8 9]的条形图')

28、绘制高斯分布函数的三维瀑布图。
>> [x,y]=meshgrid(-4:0.05:4);
>> z=peaks(x,y);
>> waterfall(x,y,z)

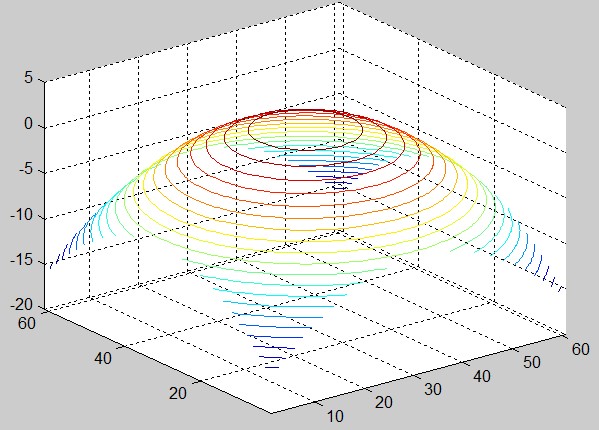
29、绘制等值线图。
>> [x,y]=meshgrid(-3:0.1:3);
>> z=2-x.^2-y.^2;
>> contour3(z,20)

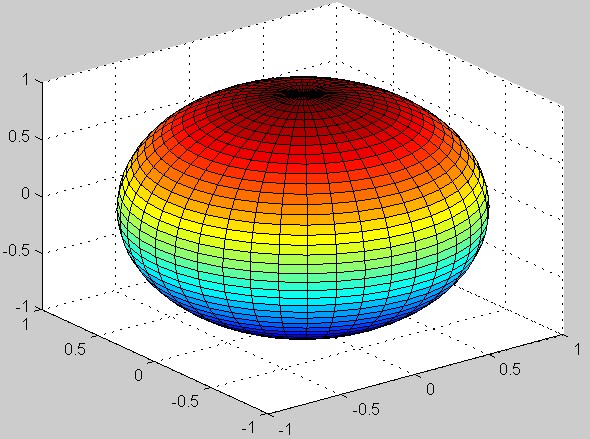
30、绘制一个球面。
>> [x,y,z]=sphere(40);
>> surf(x,y,z)

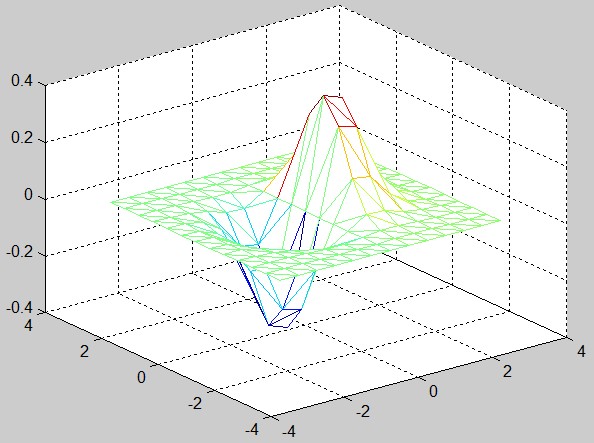
31、绘制三角形网格图和三角形表面图。
>> [x,y]=meshgrid(-3:0.5:3);
>> z=x.*exp(-x.^2-y.^2);
>> tri=delaunay(x,y);
%建立三角形网格
>> trimesh(tri,x,y,z)
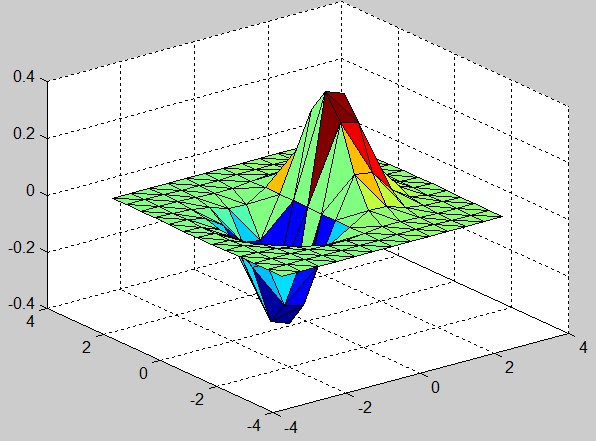
>> trisurf(tri,x,y,z)

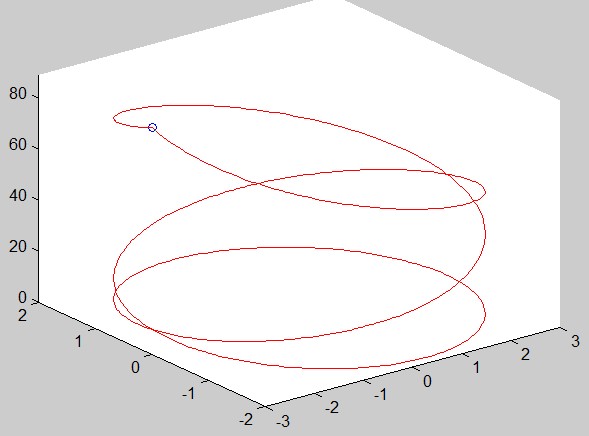
32、绘制一个三维彗星图。
>> t=[-3*pi:pi/100:3*pi];
>> x=3.*cos(t);
>> y=2.*sin(t);
>> z=t.^2;
>> comet3(x,y,z)

33、绘制曲面z的表面法向量向量图。
>> [x,y]=meshgrid([-3:0.2:3],[-2:0.5:2]);
>> z=x.*exp(-x.^2-y.*2);
>> [u,v,w]=surfnorm(x,y,z); %计算表面法向向量
>> quiver3(x,y,z,u,v,w,1.2) %绘制三维向量图
>> hold on
>> surf(x,y,z)
>> hold off

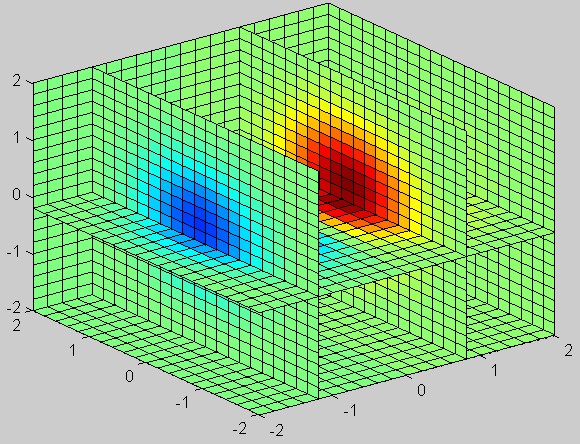
34、绘制空间立体z=xe^(-x^2-y^2-z^2 )在-2<=x<=2, -2<=y<=2, -2<=z<=2上的切片图。
>> [x,y,z]=meshgrid(-2:0.2:2);
>> v=x.*exp(-x.^2-y.^2-z.^2);
>> xi=[-1.2 0.8 2];yi=2;zi=[-2 -0.2];
>> slice(x,y,z,v,xi,yi,zi)