GLU(Gated Linear Unit) 门控线性单元

本文主要是介绍GLU(Gated Linear Unit) 门控线性单元，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

一、RNN
二、GLU
- 2.1 整体结构
- 2.2 输入层(Input Sentence+Lookup Table)
- 2.3 中间层(Convolution+Gate)
- 2.4 输出层(Softmax)
- 2.5 实验结果
- 2.6 实现代码
三、RNN与GLU的对比
参考资料

GLU可以理解为能够并行处理时序数据的CNN网络架构，即利用CNN及门控机制实现了RNN的功能。优点在进行时序数据处理时严格按时序位置保留信息从而提升了性能，并且通过并行处理结构加快了的运算速度。

一、RNN

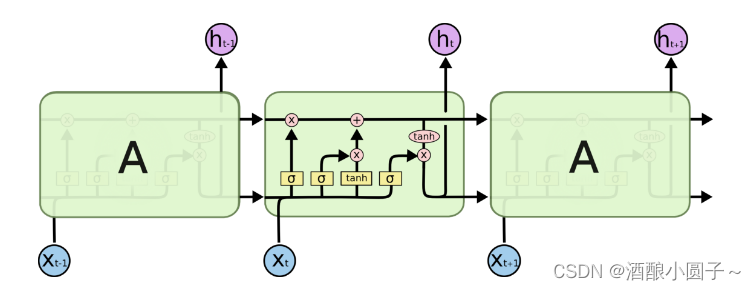
可以通过之前的博客回顾一下RNN的典型代表LSTM：RNN神经网络-LSTM模型结构
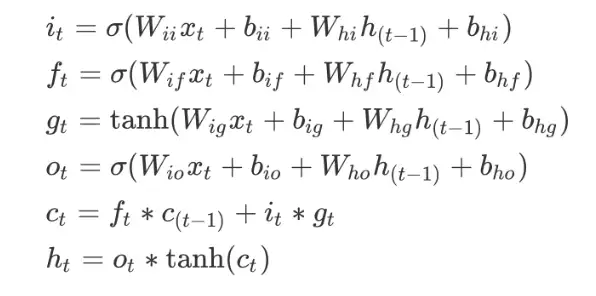
在这里插入图片描述

在这里插入图片描述

二、GLU

GLU是2016年由Yann N. Dauphin在论文《Language Modeling with Gated Convolutional Networks》中提出。

论文地址：https://arxiv.org/abs/1612.08083

2.1 整体结构

GLU在语言模型的建模方法上相比于循环神经网络更具有竞争力，它提出了一种简单的线性门控单元来堆叠卷积层从而使得文本中的 Token 可以并行化处理来获得上下文的语义特征。而且与循环神经网络相比，其复杂度从 $O (N)$ 降低到 O(N/k) ，其中的 $k$ 为卷积核的宽度， $N$ 为文本的上下文集合。论文中整个模型的结构如下图所示：
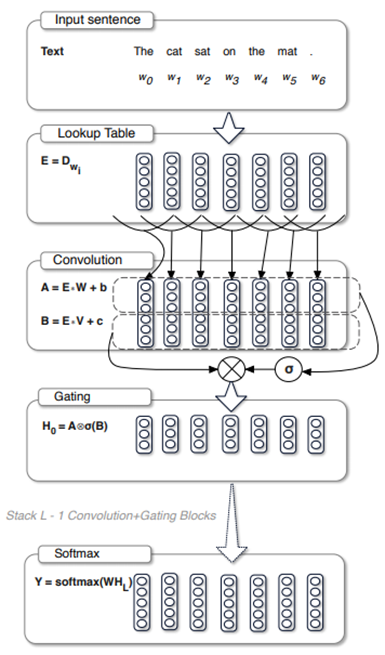
在这里插入图片描述

从上图可以清晰的看到整个模型的结构，主要也就分为三个部分：输入层(Input Sentence+Lookup Table)、中间层(Convolution+Gate)以及输出层(Softmax)，很明显的三层式结构。

2.2 输入层(Input Sentence+Lookup Table)

对于模型的输入的每个文本我们可以表示为 $W = [w_1, w_2,..., w_n]$ ，其中的 $w_1, w_2,..., w_n$ 为文本中的每个 Token ，这些 Token 在输入到模型的 embedding layer 时通过查表获取相应的向量，可表示为 $E = [e_{w1}, e_{w2},..., e_{wn}]$ ，其中 $E$ 作为该条文本的向量集合。

2.3 中间层(Convolution+Gate)

对于输入层获取的文本向量 $E = [e_{w1}, e_{w2},..., e_{wn}]$ 来说，首先输入到两个卷积层 Conv1 和 Conv2，得到两个输出 $C_{conv1}$ 和 $C_{conv2}$ ，然后将 $C_{conv2}$ 输入到激活函数 Sigmoid 中，然后通过Hadamard积逐位相乘得到相应的隐层向量 $h$ ，更一般的可表示为：

在这里插入图片描述

到这里可以看出，门控线性单元与LSTM的门控本质上是一样的，只不过在计算隐层向量时不需要依赖上一个时间步。通过堆叠多层卷积就可以得到文本的上下文信息。

作者还提出了一种GTU的门控机制，其实也就是将GLU的前一项利用 tanh 函数进行激活，但多引入一个激活函数就代表梯度在反向传播过程中就多了一项衰减项，因此，作者认为GLU优于GTU。GTU表示为：
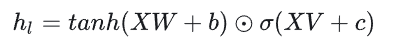
在这里插入图片描述

2.4 输出层(Softmax)

输出层采用了 softmax 函数，将神经元的输出映射到 $[0, 1]$ 的区间，并且满足所有输出的和为1。对于语言模型建模而言，其词表为 $V$ ， $v_i$ 则表示词表中的第 $i$ 个词语，那么语言模型在预测到这个词语的概率经过 softmax 归一化就为：
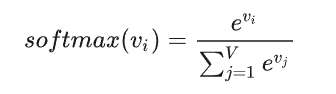
在这里插入图片描述

2.5 实验结果

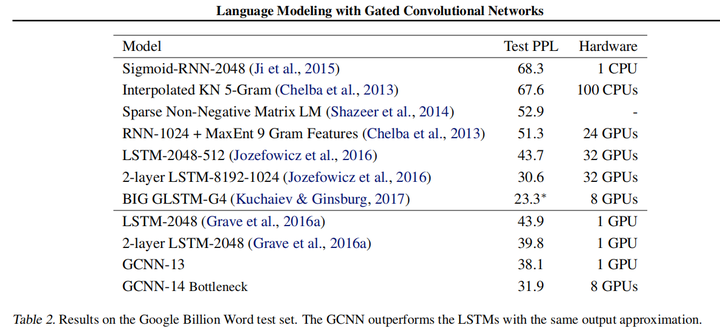
在这里插入图片描述

从图上可以看出，在相同的计算资源的条件下，GCNN-13的困惑度小于2层神经元数为2048的LSTM模型，由此可以看出GCNN的优越性，并且GCNN是可以并行计算的。

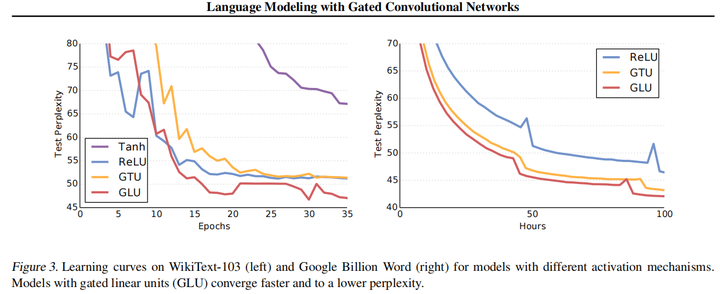
在这里插入图片描述
将门控线性单元GLU与其他机制以及没有门控的模型进行比较，可以明显看出GLU在模型收敛时更快，并且困惑度是比较低的。

2.6 实现代码

import torch
import torch.nn as nnclass GateLinearUnit(nn.Module):def __init__(self, embedding_size, num_filers, kernel_size, vocab_size, bias=True, batch_norm=True, activation=nn.Tanh()):super(GateLinearUnit, self).__init__()self.batch_norm = batch_normself.activation = activationself.embedding = nn.Embedding(vocab_size, embedding_size)self.conv_layer1 = nn.Conv2d(1, num_filers, (kernel_size, embedding_size), bias=bias)self.conv_layer2 = nn.Conv2d(1, num_filers, (kernel_size, embedding_size), bias=bias)self.batch_norm = nn.BatchNorm2d(num_filers)self.sigmoid = nn.Sigmoid()nn.init.kaiming_uniform_(self.conv_layer1.weight)nn.init.kaiming_uniform_(self.conv_layer2.weight)def gate(self, inputs):"""门控机制"""return self.sigmoid(inputs)def forward(self, inputs):embed = self.embedding(inputs)embed = embed.unsqueeze(1)output = self.conv_layer1(embed)gate_output = self.conv_layer2(embed)# Gate Operationif self.activation is not None:# GTUoutput = self.activation(output) * self.gate(gate_output)else:# GLUoutput = output * self.gate(gate_output)if self.batch_norm:output = self.batch_norm(output)output = output.squeeze()return outputelse:return output.squeeze()if __name__=="__main__":x = torch.randint(1,100,[32, 128])glu = GateLinearUnit(embedding_size=300, num_filers=256, kernel_size=3, vocab_size=1000)out = glu(x)

三、RNN与GLU的对比

GLU是能够并行处理时序数据的CNN网络架构，即利用CNN及门控机制实现了RNN的功能。优点在进行时序数据处理时严格按时序位置保留信息从而提升了性能，并且通过并行处理结构加快了的运算速度。

GLU与RNN的结构不同才实现了功能不同，主要有两个区别，一个相同点：

在是否使用时间窗口上不同。RNN与LSTM并不存在时间窗口概念，直接对时序数据进行迭代式处理，至序列结束；而GLU使用了时间窗口，与Transformer类似，只能处理定长的时序数据。
在是否使用了卷积运算上不同。RNN不存在卷积运算，对于时序数据的处理机制是不断将当前时刻的信息加工处理，逐个添加至隐藏层中信息；而GLU使用了卷积运算，主要目标是将时间窗口内当前时刻之前的所有信息进行压缩，由于信息时序位置与实际内容均未发生变化，因而使可以用CNN直接并行处理各时刻的信息数据。
在是否使用了门结构上相同。GLU与LSTM均使用了输出门的结构，但略去了LSTM中的遗忘门与写入门，通过输出门实现了基于时序信息位置对内容输出的控制，达到了理想地输出效果。