本文主要是介绍scikit-learn linearRegression 1.1.2 岭回归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Ridge 岭回归通过对回归稀疏增加罚项来解决 普通最小二乘法 的一些问题.岭回归系数通过最小化带罚项的残差平方和

上述公式中,  是控制模型复杂度的因子(可看做收缩率的大小) :
是控制模型复杂度的因子(可看做收缩率的大小) :  越大,收缩率越大,那么系数对于共线性的鲁棒性更强
越大,收缩率越大,那么系数对于共线性的鲁棒性更强

一、一般线性回归遇到的问题
在处理复杂的数据的回归问题时,普通的线性回归会遇到一些问题,主要表现在:
- 预测精度:这里要处理好这样一对为题,即样本的数量
和特征的数量
时,最小二乘回归会有较小的方差
时,容易产生过拟合
时,最小二乘回归得不到有意义的结果
- 模型的解释能力:如果模型中的特征之间有相互关系,这样会增加模型的复杂程度,并且对整个模型的解释能力并没有提高,这时,我们就要进行特征选择。
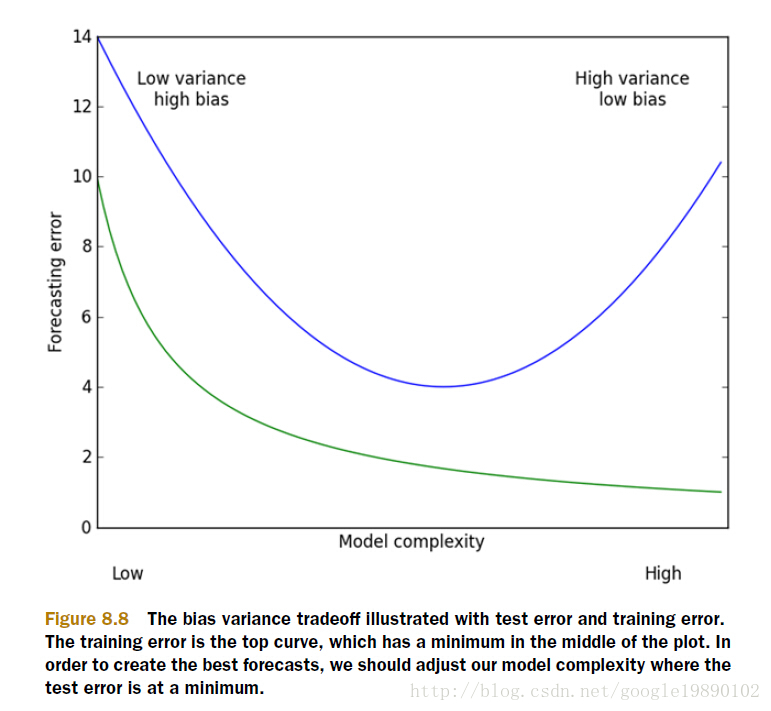
以上的这些问题,主要就是表现在模型的方差和偏差问题上,这样的关系可以通过下图说明:
(摘自:机器学习实战)
方差指的是模型之间的差异,而偏差指的是模型预测值和数据之间的差异。我们需要找到方差和偏差的折中。
二、岭回归的概念
在进行特征选择时,一般有三种方式:
- 子集选择
- 收缩方式(Shrinkage method),又称为正则化(Regularization)。主要包括岭回归和lasso回归。
- 维数缩减
,
通过确定的值可以使得在方差和偏差之间达到平衡:随着
的增大,模型方差减小而偏差增大。
对求导,结果为
令其为0,可求得的值:
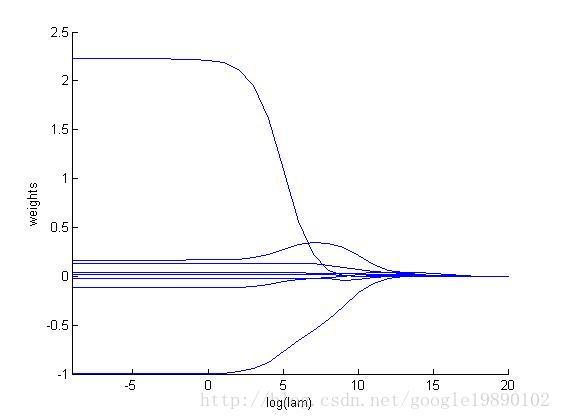
三、实验的过程
我们去探讨一下取不同的对整个模型的影响。
和其他线性模型一样,Ridge 调用 fit 方法,参数为X,y,并且将线性模型拟合的系数  存到成员变量
存到成员变量 coef_中。:
Classifier using Ridge regression.
Read more in the User Guide.
| Parameters: | alpha : float
class_weight : dict or ‘balanced’, optional
copy_X : boolean, optional, default True
fit_intercept : boolean
max_iter : int, optional
normalize : boolean, optional, default False
solver : {‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’}
tol : float
random_state : int seed, RandomState instance, or None (default)
|
|---|---|
| Attributes: | coef_ : array, shape (n_features,) or (n_classes, n_features)
intercept_ : float | array, shape = (n_targets,)
n_iter_ : array or None, shape (n_targets,)
|
See also
Ridge, RidgeClassifierCV
Notes
For multi-class classification, n_class classifiers are trained in a one-versus-all approach. Concretely, this is implemented by taking advantage of the multi-variate response support in Ridge.
Methods
decision_function(X) | Predict confidence scores for samples. |
fit(X, y[, sample_weight]) | Fit Ridge regression model. |
get_params([deep]) | Get parameters for this estimator. |
predict(X) | Predict class labels for samples in X. |
score(X, y[, sample_weight]) | Returns the mean accuracy on the given test data and labels. |
set_params(\*\*params) | Set the parameters of this estimator. |
__init__(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, class_weight=None, solver='auto', random_state=None)[source]Predict confidence scores for samples.
The confidence score for a sample is the signed distance of that sample to the hyperplane.
Parameters: X : {array-like, sparse matrix}, shape = (n_samples, n_features)
Samples.
Returns: array, shape=(n_samples,) if n_classes == 2 else (n_samples, n_classes) :
Confidence scores per (sample, class) combination. In the binary case, confidence score for self.classes_[1] where >0 means this class would be predicted.
decision_function(X)[source]Fit Ridge regression model.
Parameters: X : {array-like, sparse matrix}, shape = [n_samples,n_features]
Training data
y : array-like, shape = [n_samples]
Target values
sample_weight : float or numpy array of shape (n_samples,)
Sample weight.
New in version 0.17: sample_weight support to Classifier.
Returns: self : returns an instance of self.
fit(X, y, sample_weight=None)[source]Get parameters for this estimator.
Parameters: deep : boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
get_params(deep=True)[source]Predict class labels for samples in X.
Parameters: X : {array-like, sparse matrix}, shape = [n_samples, n_features]
Samples.
Returns: C : array, shape = [n_samples]
Predicted class label per sample.
predict(X)[source]Returns the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True labels for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
Mean accuracy of self.predict(X) wrt. y.
score(X, y, sample_weight=None)[source]Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.
set_params(**params)[source]这篇关于scikit-learn linearRegression 1.1.2 岭回归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!