本文主要是介绍多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法 学习记录03——机械臂运动学逆解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
系列文章目录
本科毕设正在做多轴机械臂相关的内容,这里是一个学习机械臂运动学课程的相关记录。
如有任何问题,可发邮件至layraliu@foxmail.com问询。
1. 数学基础
2. 机械臂几何法与DH表示法
3. 机械臂运动学逆解
文章目录
- 系列文章目录
- 一、引言
- 1.手臂顺向运动学forward kinematics(FK)
- 2.手臂逆向运动学inverse kinematics(IK)
- 二、求解概念
- 1.概念1
- 2.概念2
- 3.概念3
- 三、多重解
- 1.解的数目
- 2.puma(6 rotational joints)
- 3.解的选择方式
- 四、求解方法
- 1.解析法(closed-form solutions)
- 2.数值法(numerical solutions)
- 3.A RRR Manipulator
- 4.A Pieper’s Solution
- 五、一般的例子
- 1.坐标系
- 2.物件取放任务
- 总结
一、引言
1.手臂顺向运动学forward kinematics(FK)
正运动学(forward kinematics)是从关节变量θ到坐标系{b}在坐标系{s}中的位置和方向的映射T(θ)。
即,正运动学是通过 Joints 的转动角度或移动距离来推算末端执行器的位姿。
2.手臂逆向运动学inverse kinematics(IK)
逆向运动学刚好相反,是由末端执行器的位姿来推算 Joints 的状态。

二、求解概念
1.概念1
假设手臂有6 DOFs,则有:
在H frame中提取出16个数字,其中:转动9个数字,第六个frame的原点相对于第零个点位移量3个数字。
转动的9个数字:3个自由度,6个限制条件(三个列向量之间两两垂直——三个约束条件;秩为3——三个约束条件)。
位移的3个数字:独立,3个自由度

求解:
12个nonlinear transcendental 方程式。(非线性超越方程组)
2.概念2
reachable workspace可达空间:手臂可以用一种以上的姿态到达的位置。
dexterous workfare灵巧空间:手臂可以用任何的姿态到达的位置。
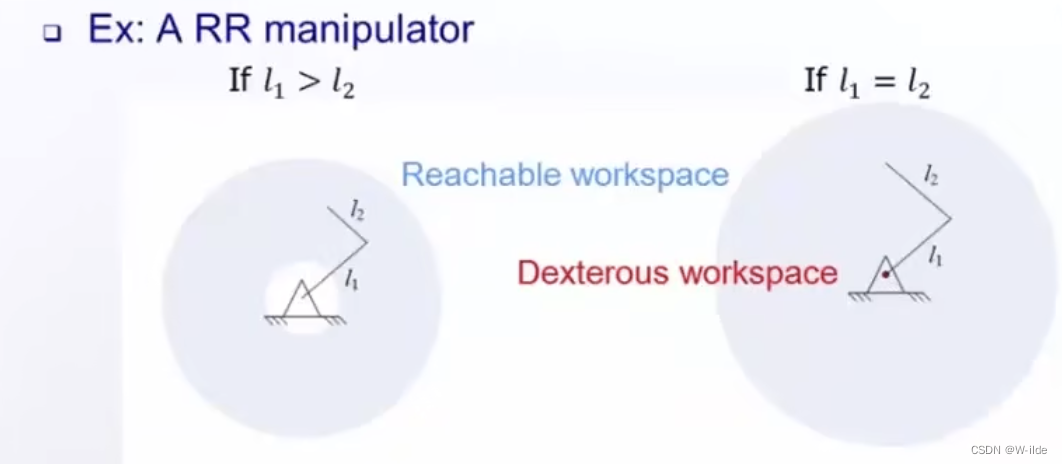
原点为dexterous workspace(360度)
3.概念3
subspace:手臂在定义头尾的T所能到达的变动范围
(如下就只有一个)
若x和y确定,左上角旋转矩阵就定下来了,没有多余的解。
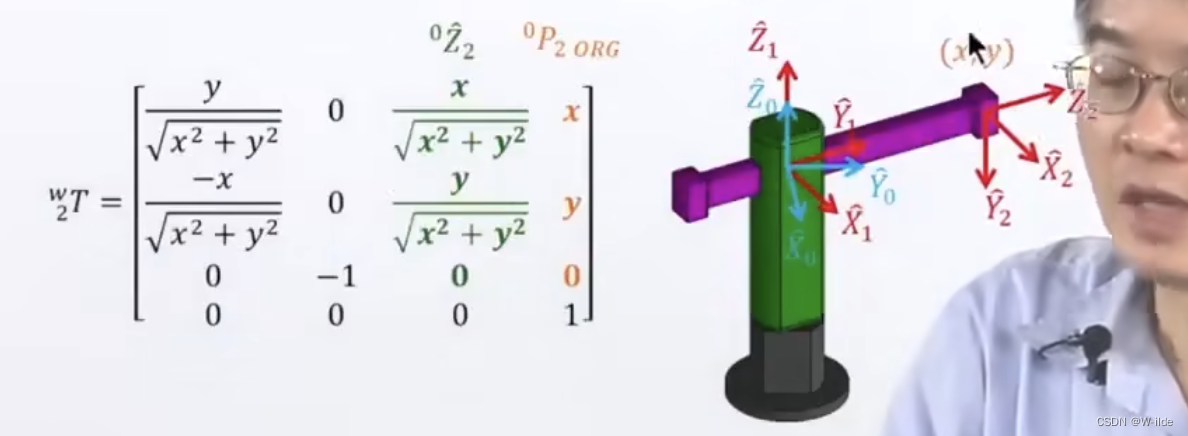
三、多重解
1.解的数目
由于是非线性超越方程,所以六个未知数六个方程不代表有唯一解。
(6个未知数、6个限制条件)
是由joint和link参数所决定的。

2.puma(6 rotational joints)
针对一个特定工作点,有八组解;
前3个轴具有4种姿态;
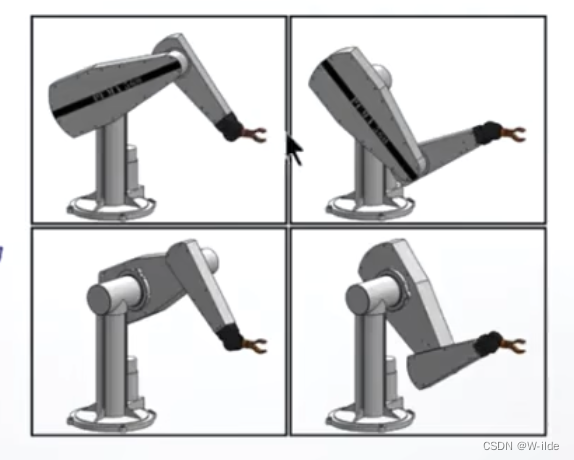
每一个姿态中,具有2组手腕转动姿态。
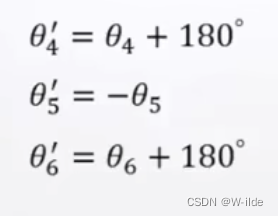
但若手臂本身有几何限制,并非每一种解都可以运作。
3.解的选择方式
选择:离目前状态最近的解
最快/最省能;
避开障碍物。
四、求解方法
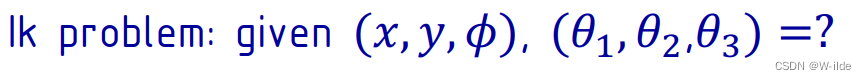
1.解析法(closed-form solutions)
代数法/几何法
目前大多数机械手臂都设计成具有解析解,即pieper’s solution,相邻三轴相交于一点。
2.数值法(numerical solutions)
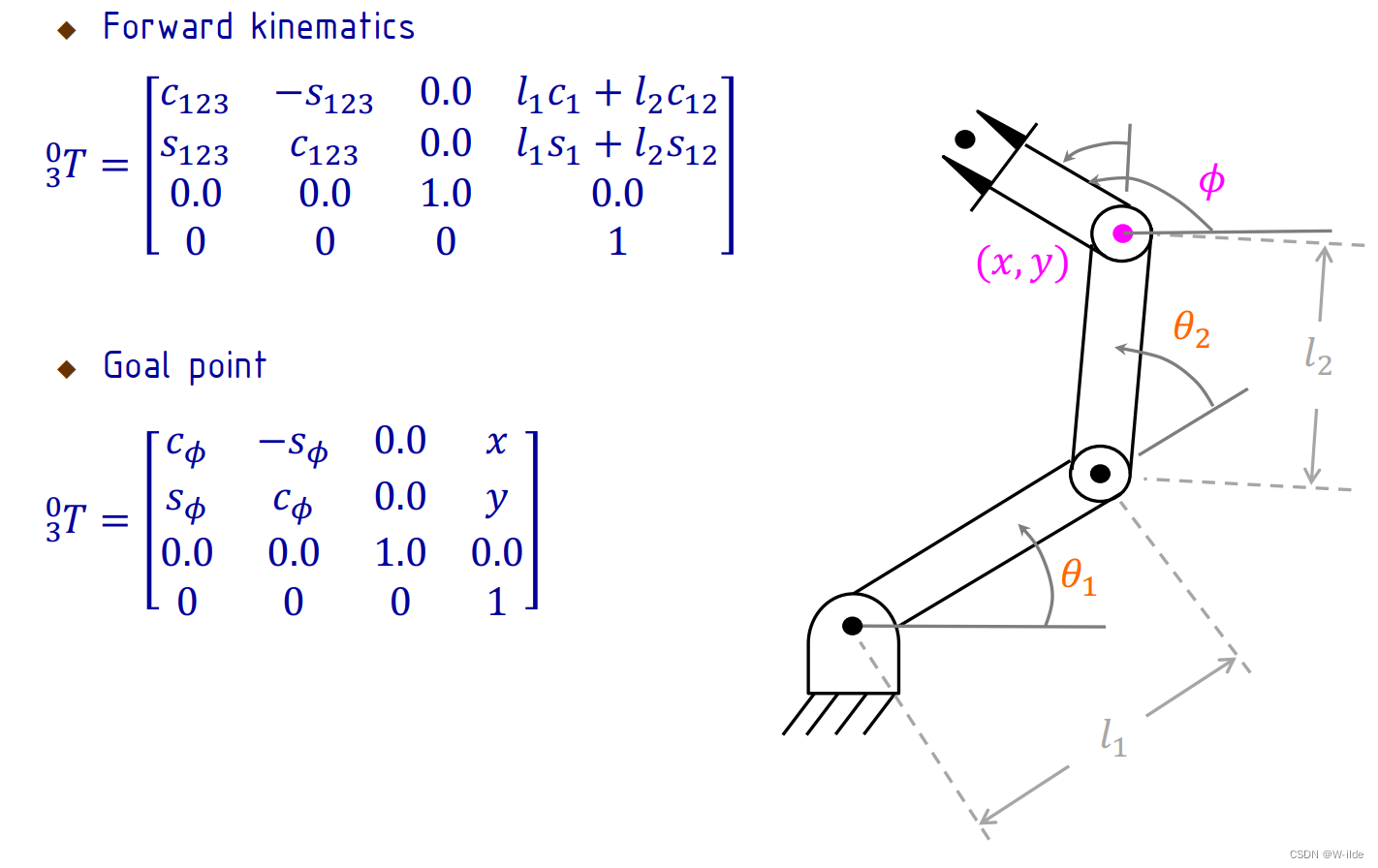
3.A RRR Manipulator
(已知是红色的,未知是橙色的)
附:

- 几何法
将空间几何切割成平面几何。划分成平面几何后,按正弦、余弦定律等找解。
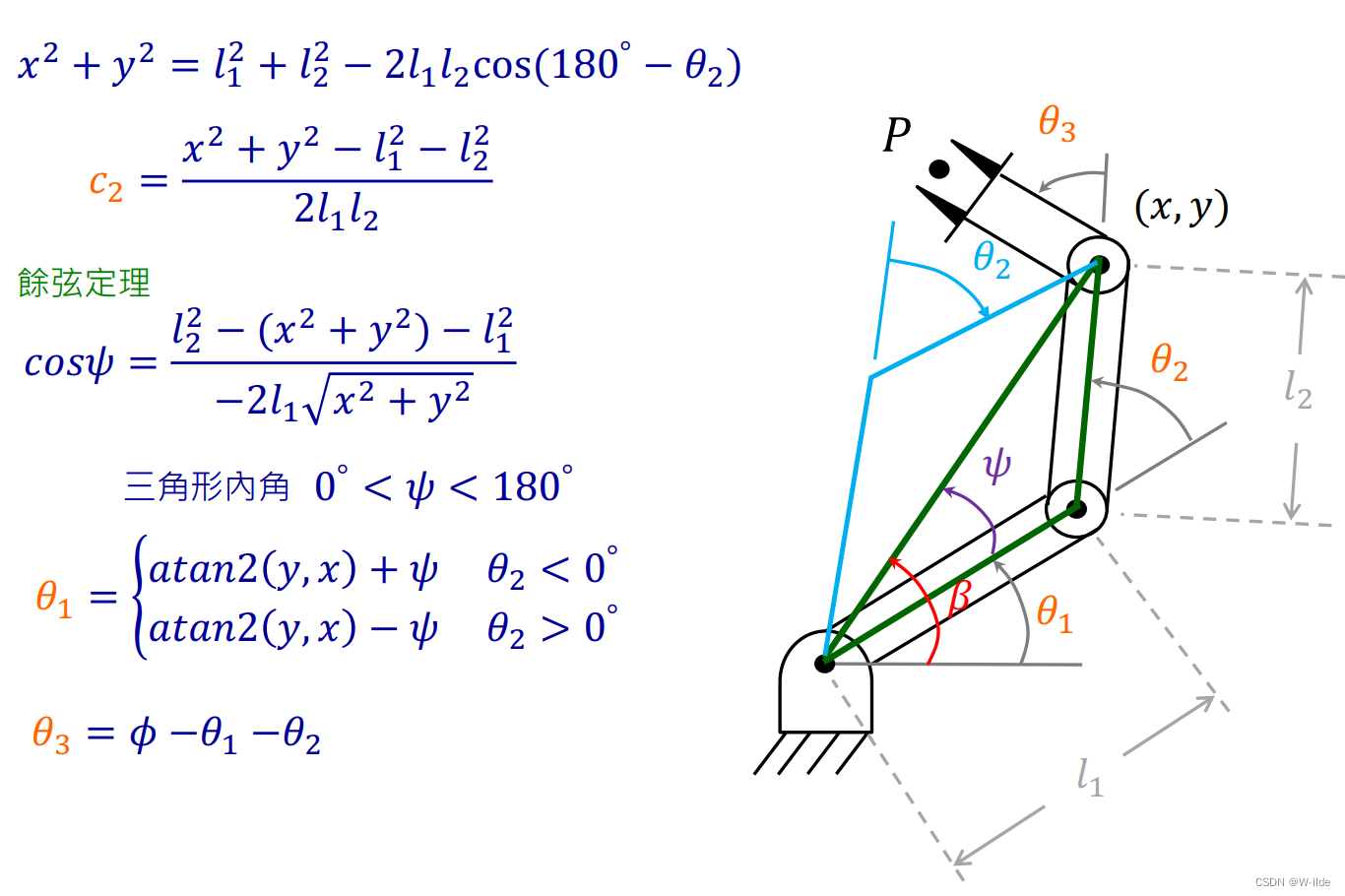
量化计算
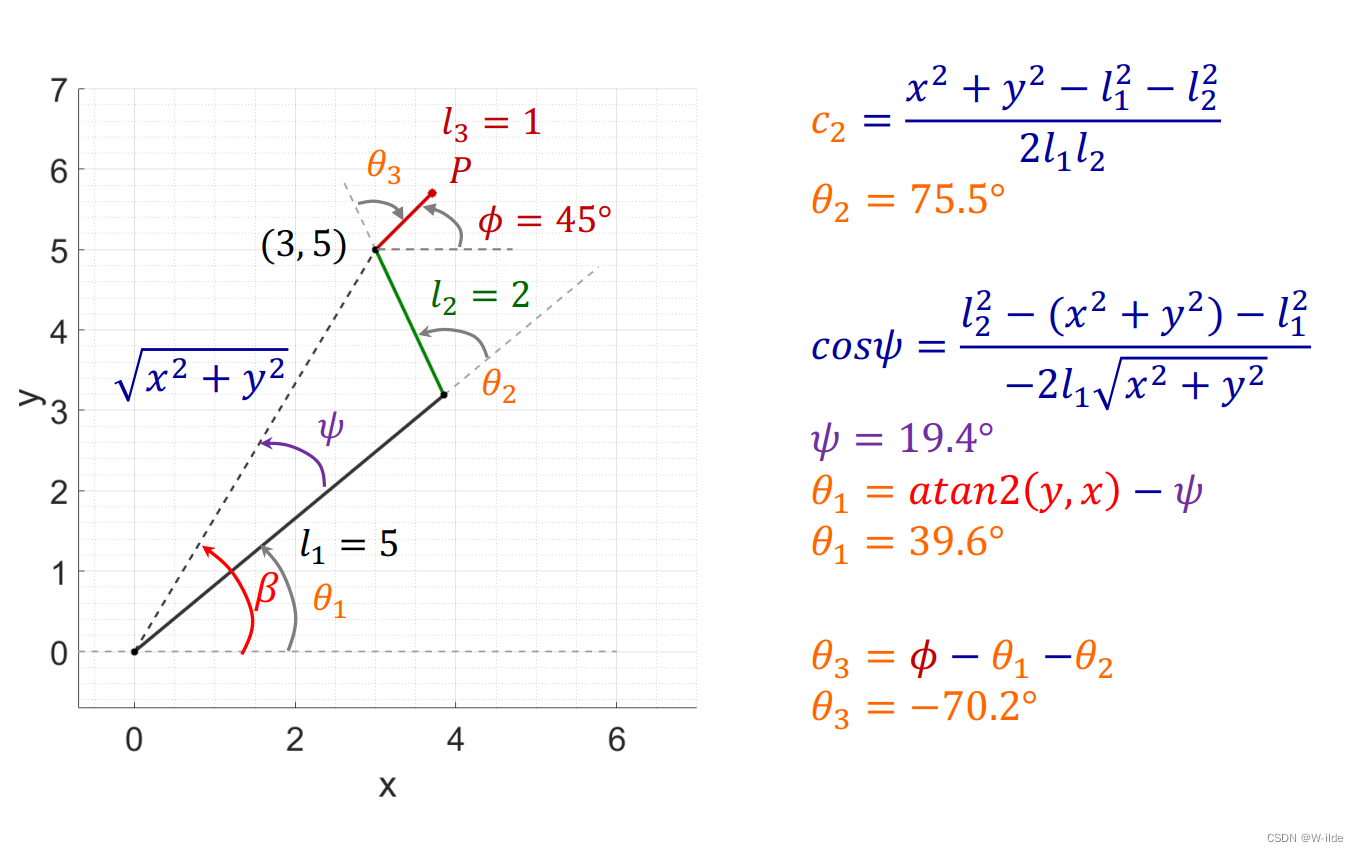
- 代数解

注意这里theta 2是双解

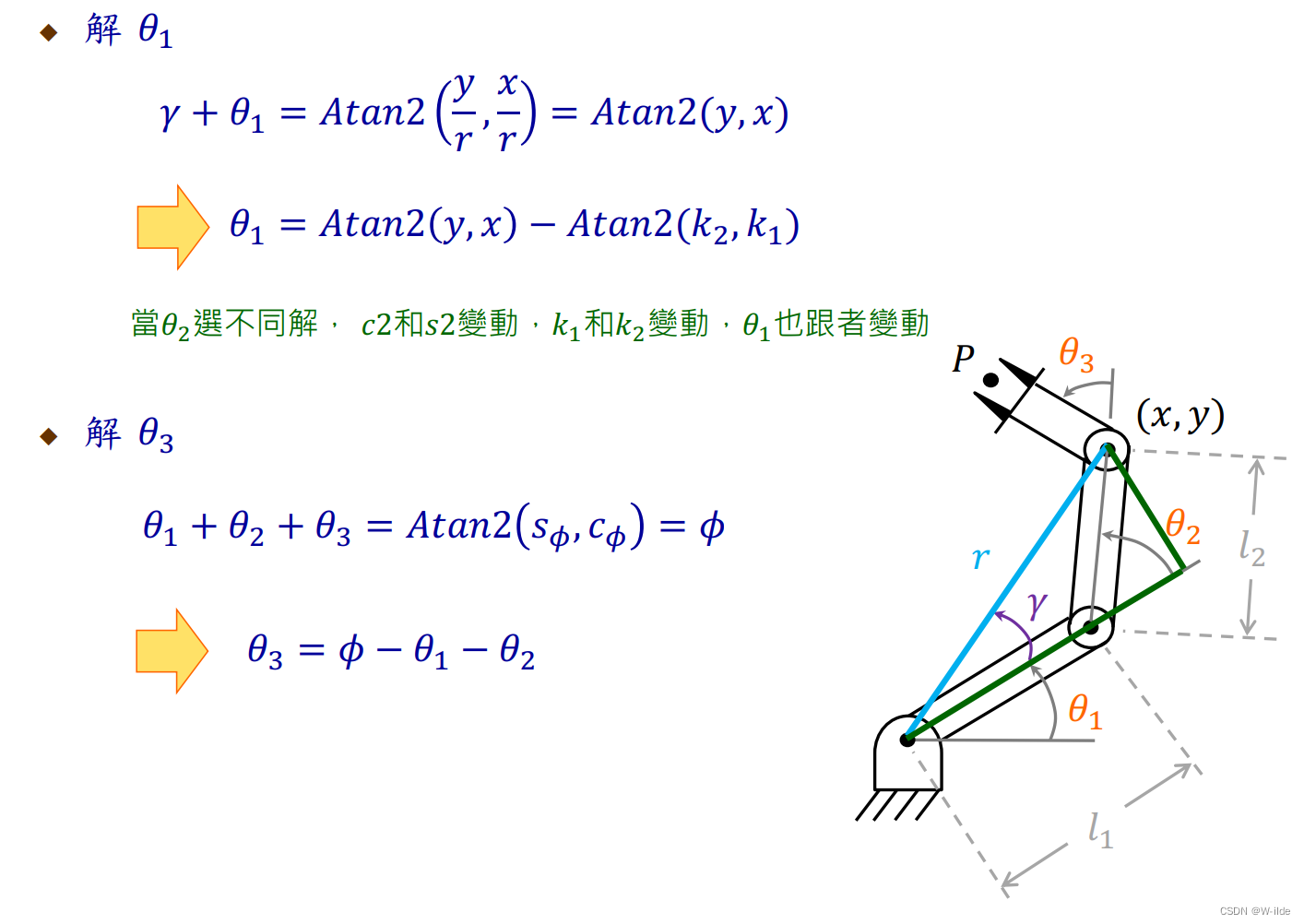
一个数学问题:(理解为高数里的万能公式)

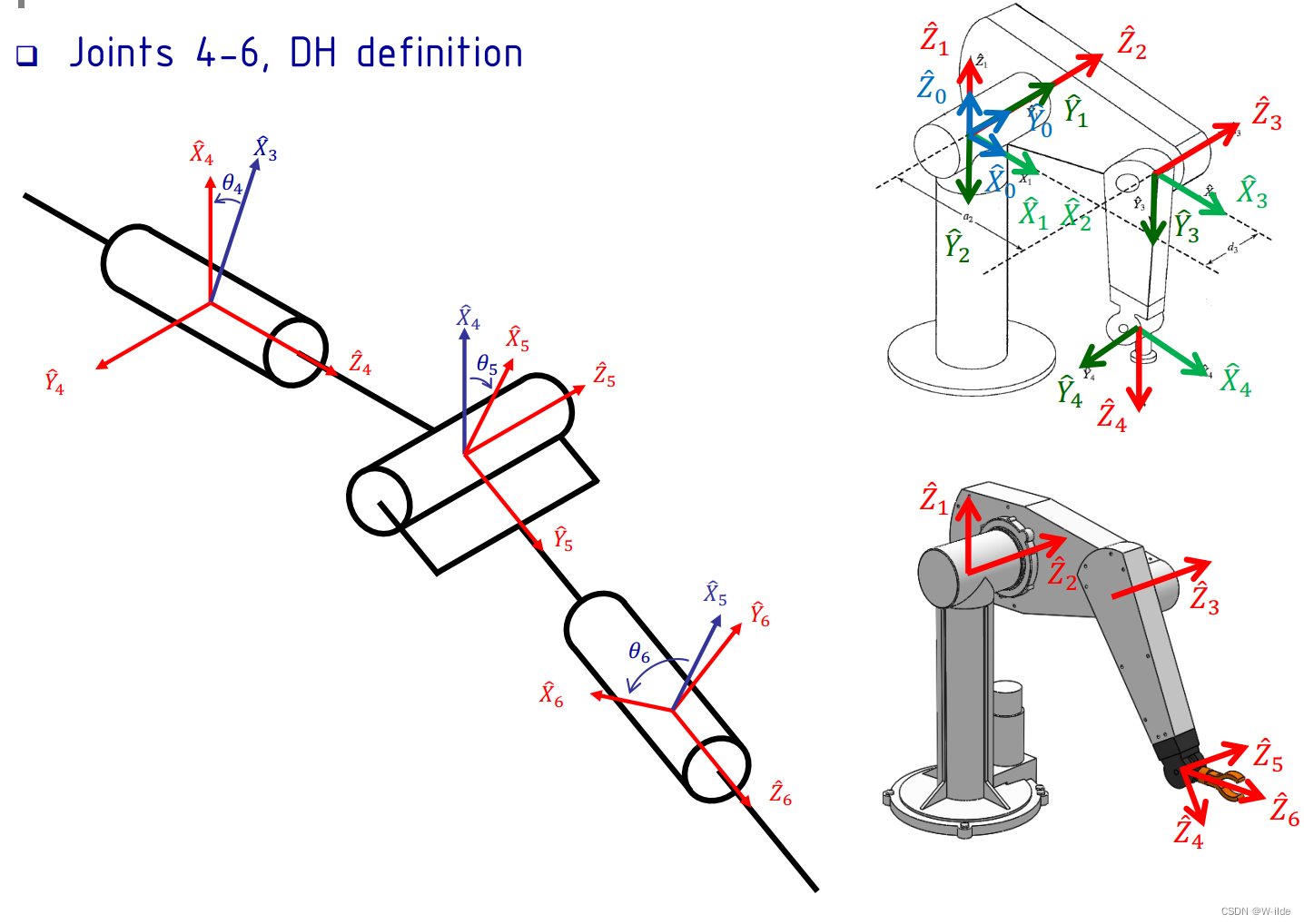
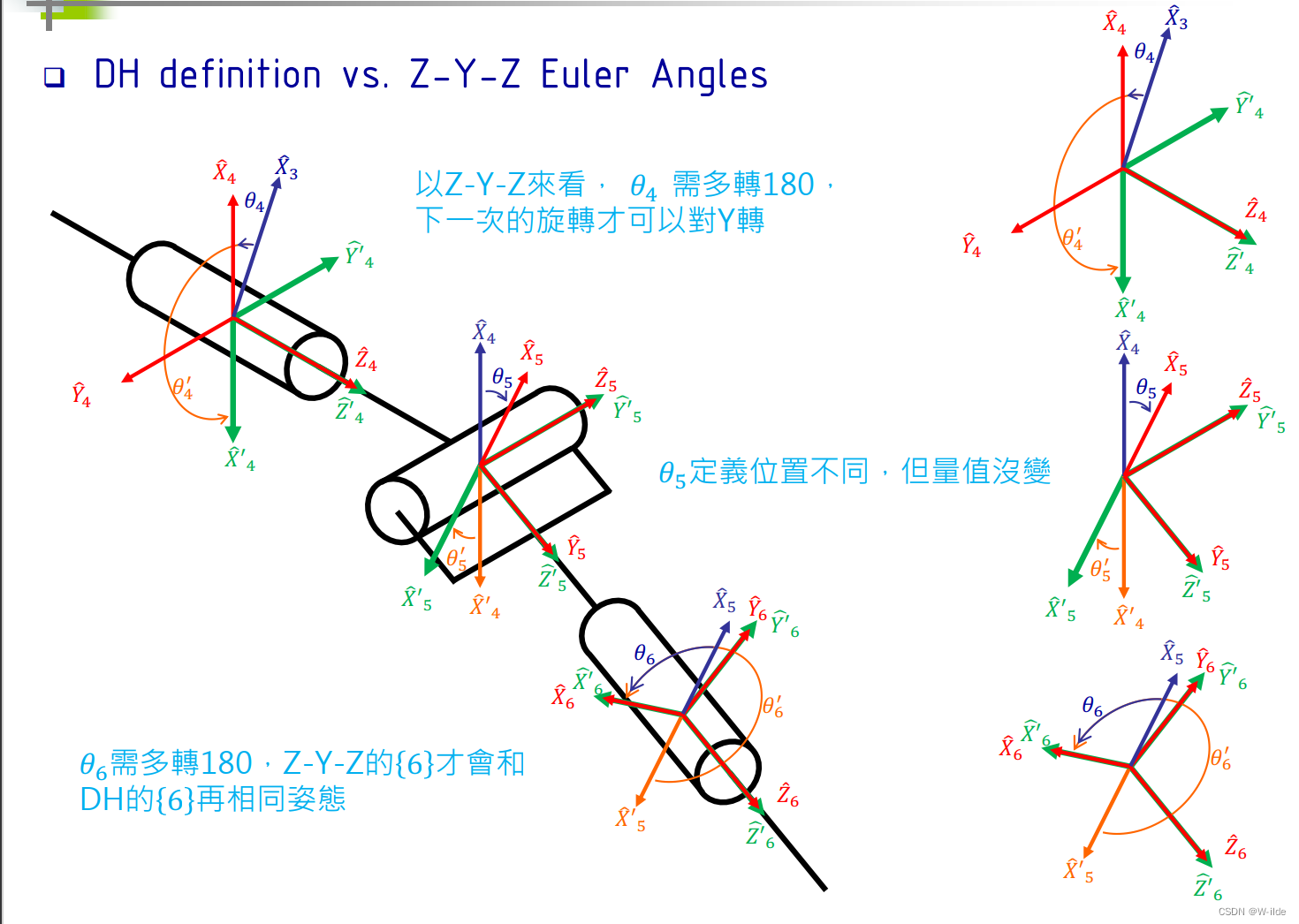
4.A Pieper’s Solution
若6DOFs具有三个连续的轴相交于一点,则手臂有解析解。
一般来说,会把最后三轴如此设计。(例如puma)
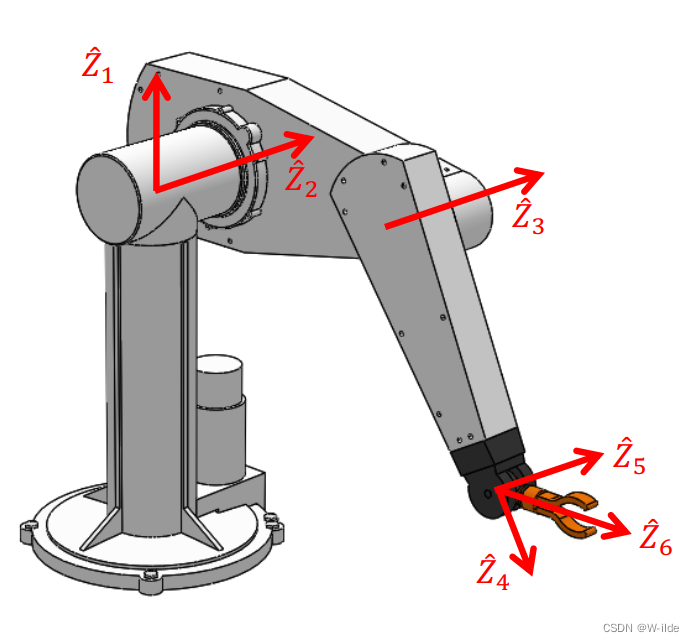
前三轴:产生移动;
后三轴:产生转动。
因为三轴交一点,所以:
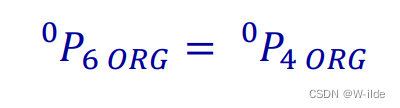
以下为解析过程:
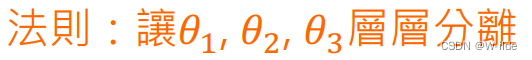

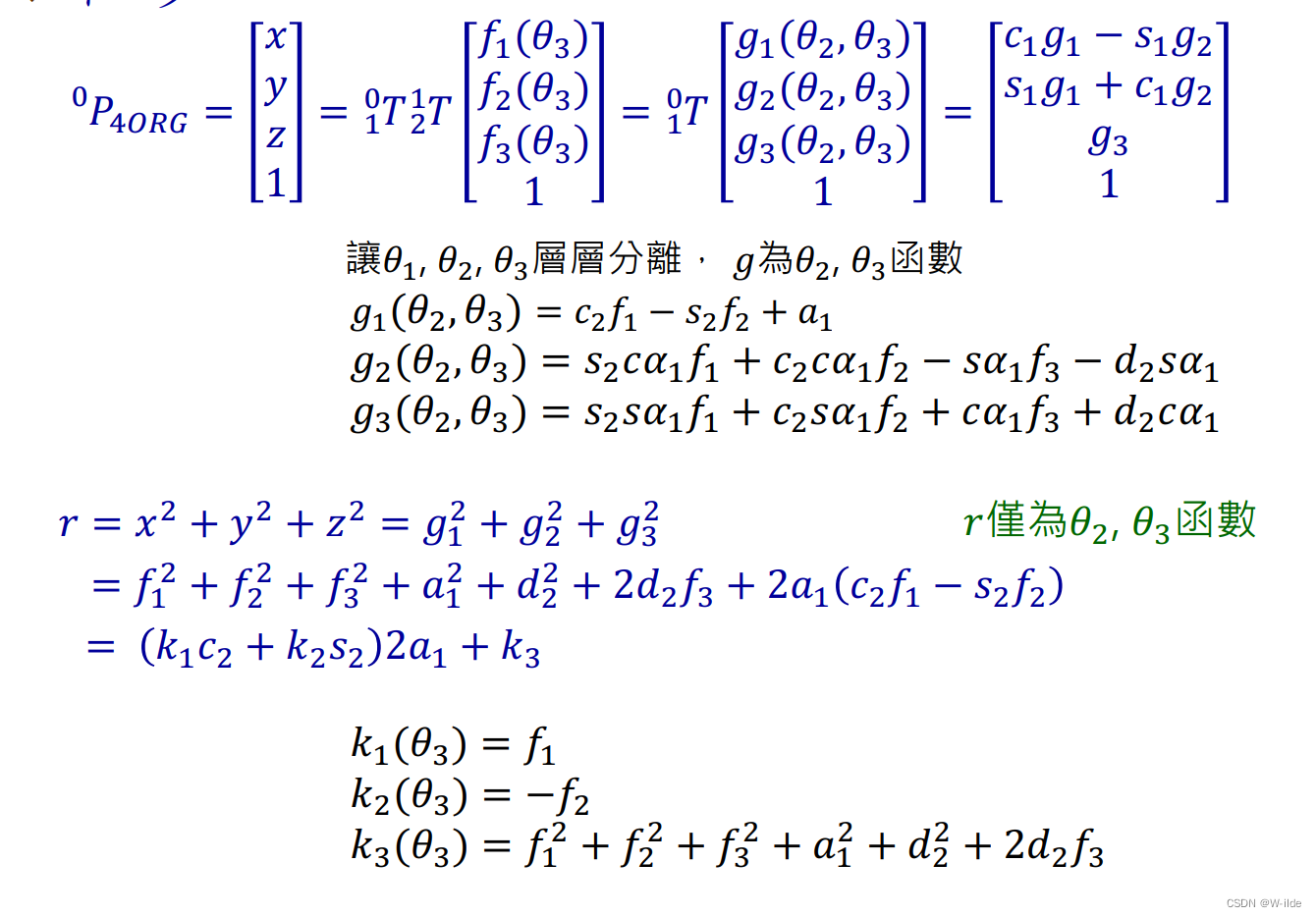


五、一般的例子
1.坐标系
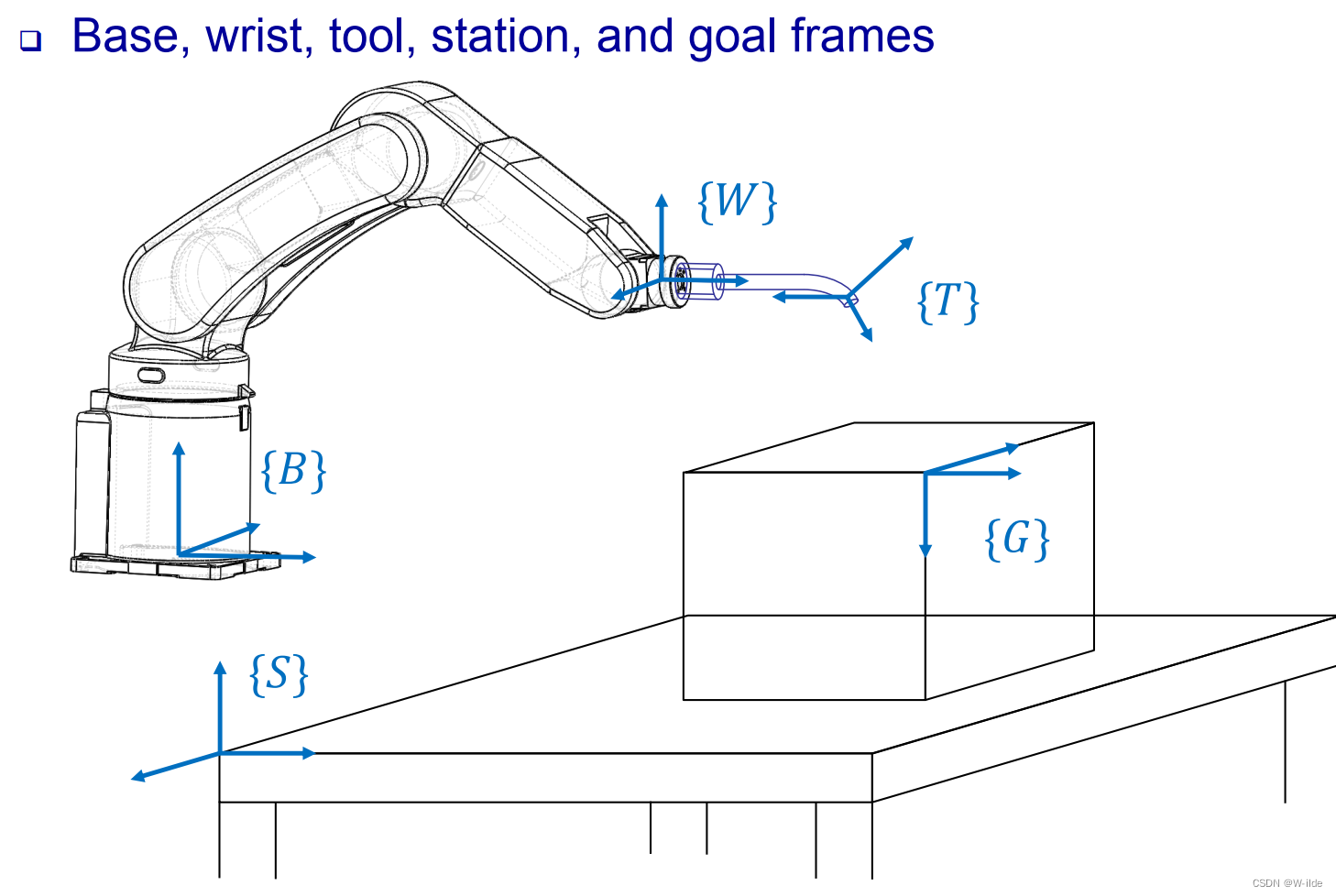
2.物件取放任务
情景:机械手臂夹住放在桌子的杯子,移动手臂将杯子挂到墙上的杯架。
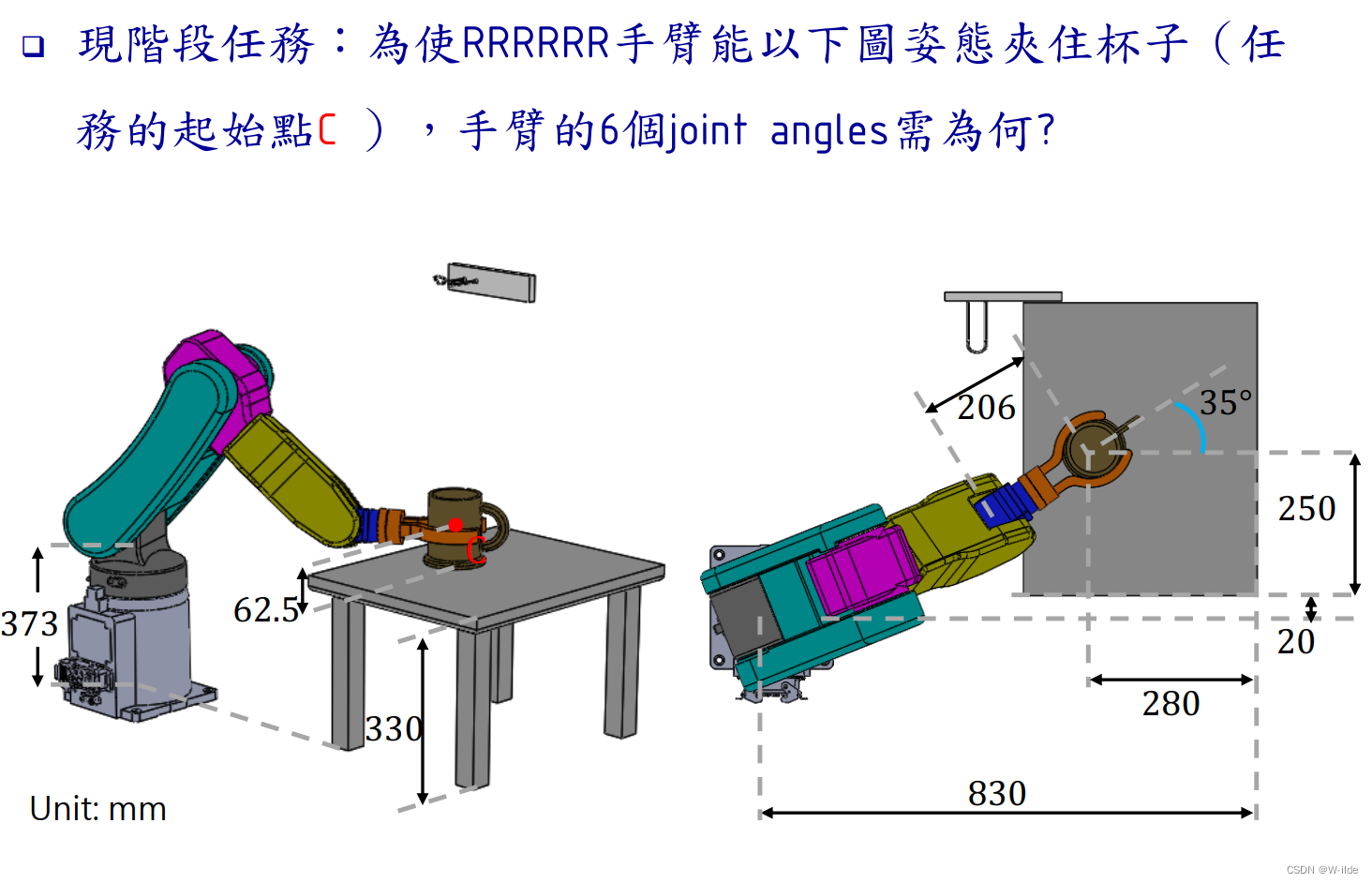
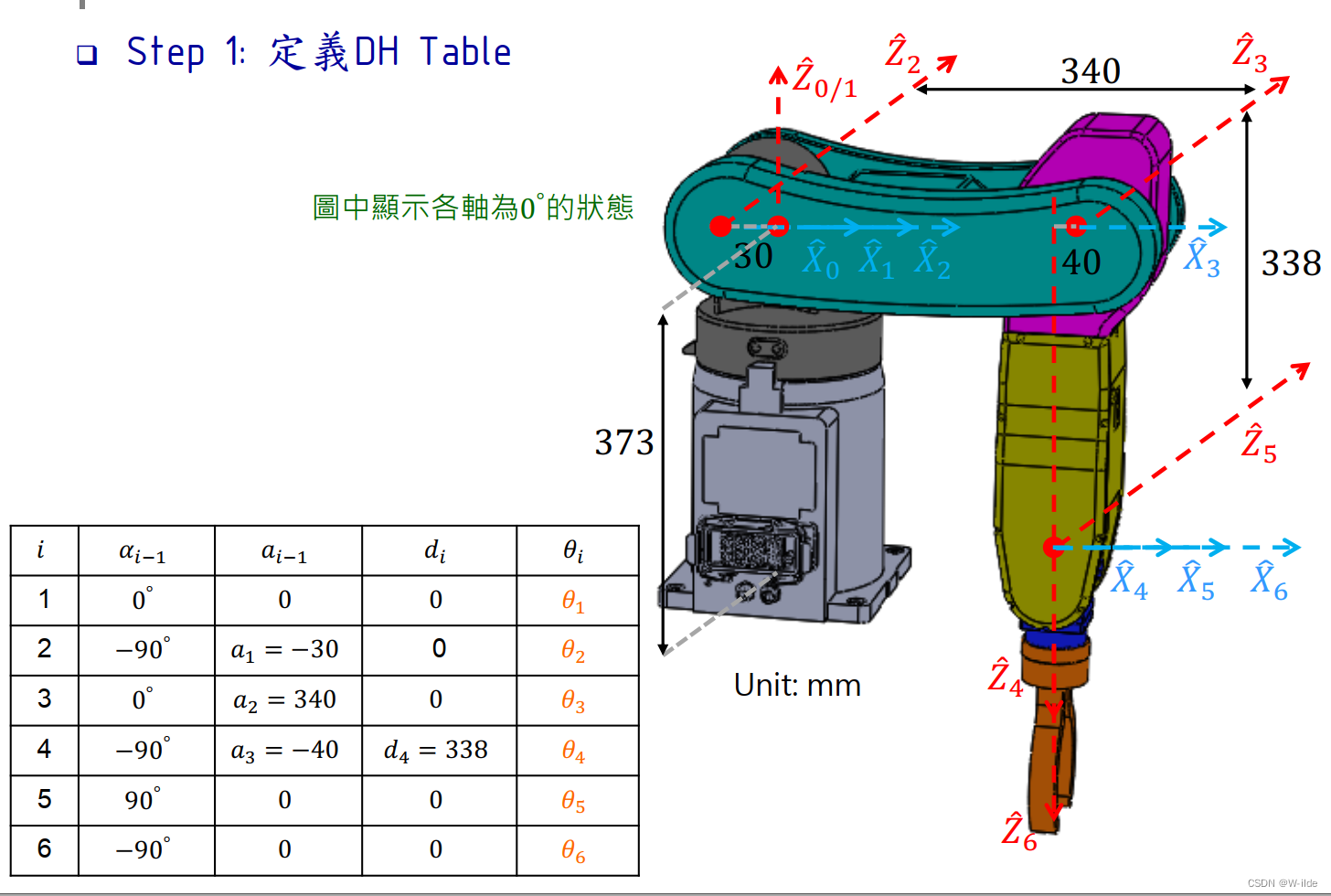
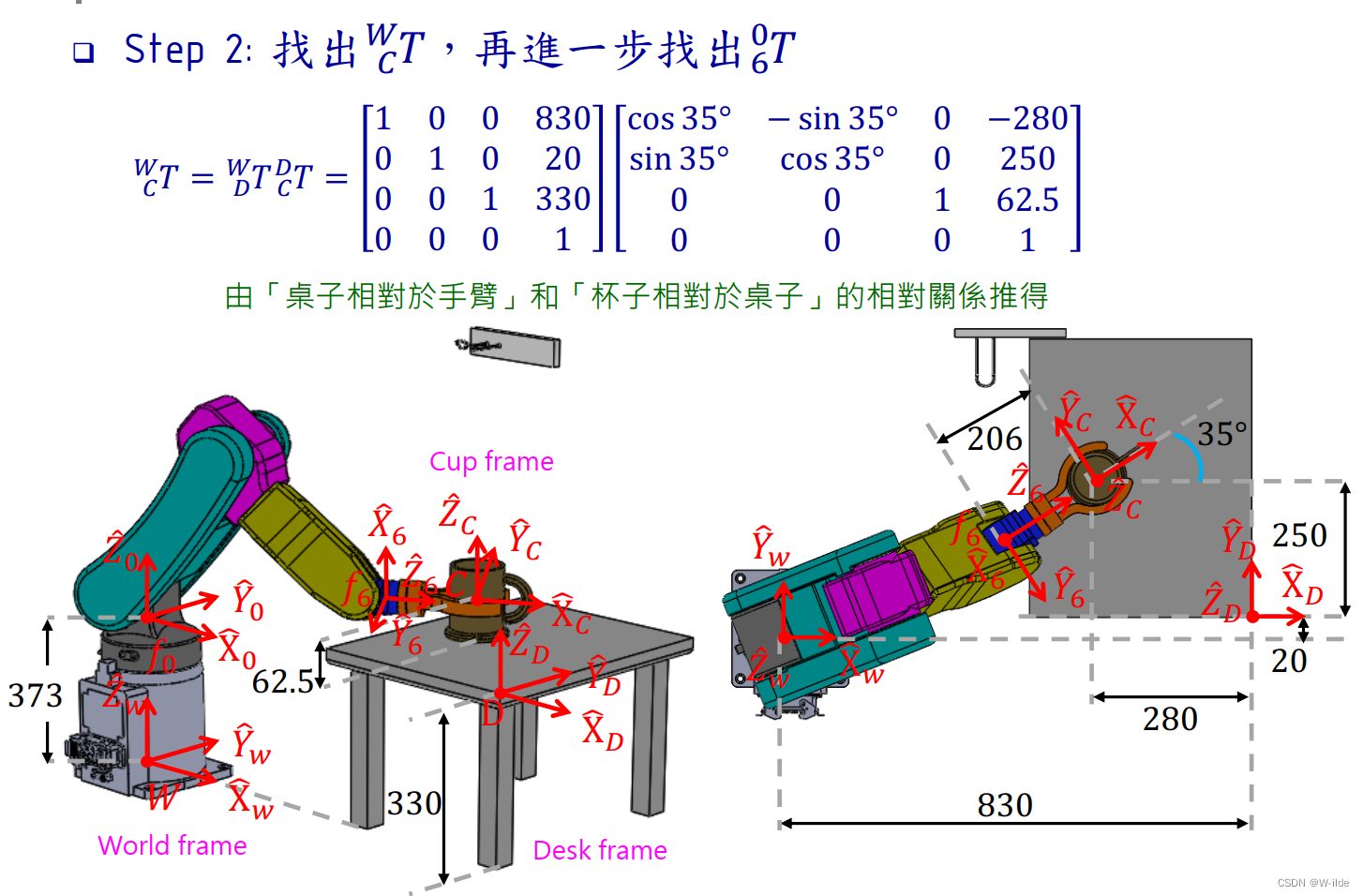
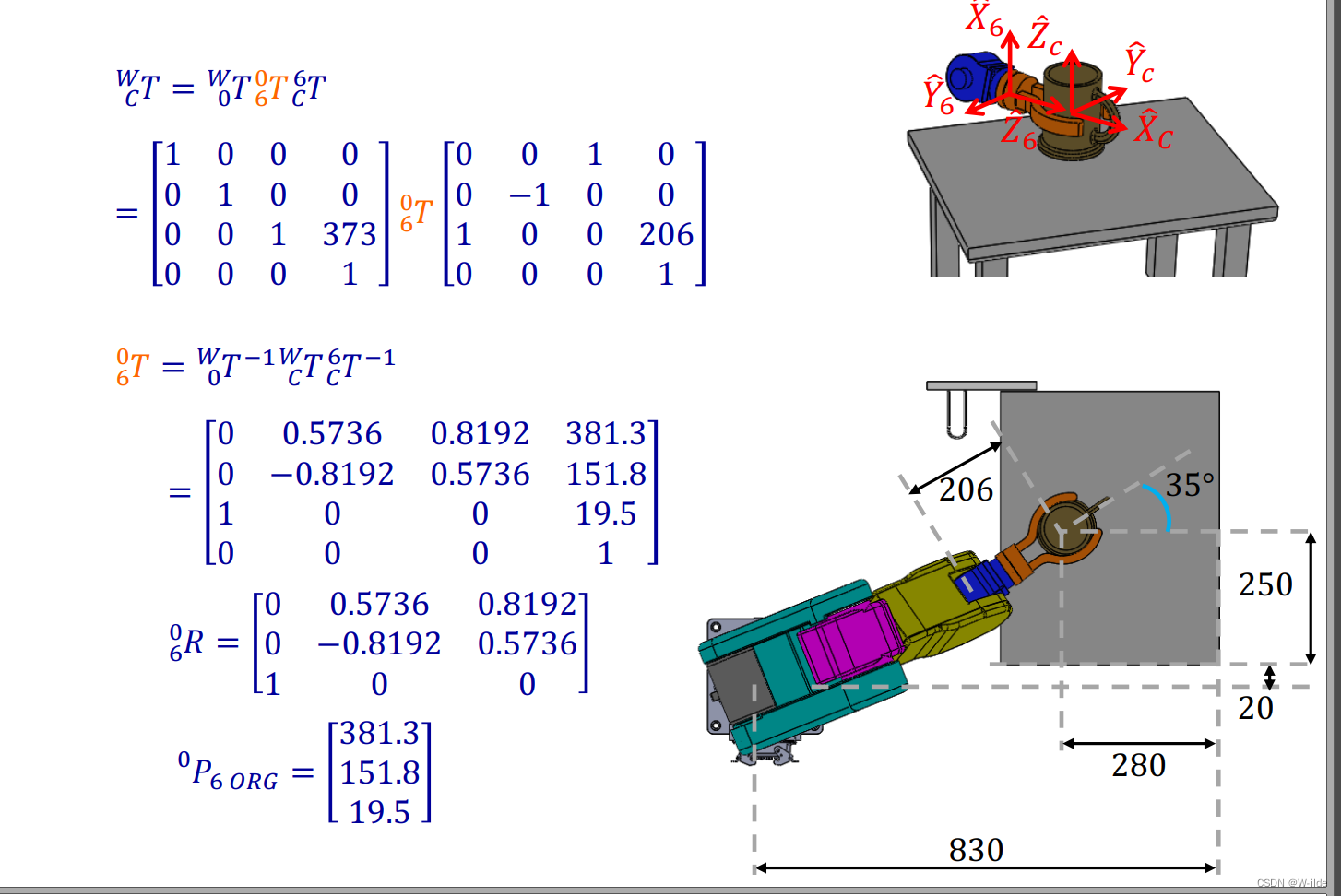

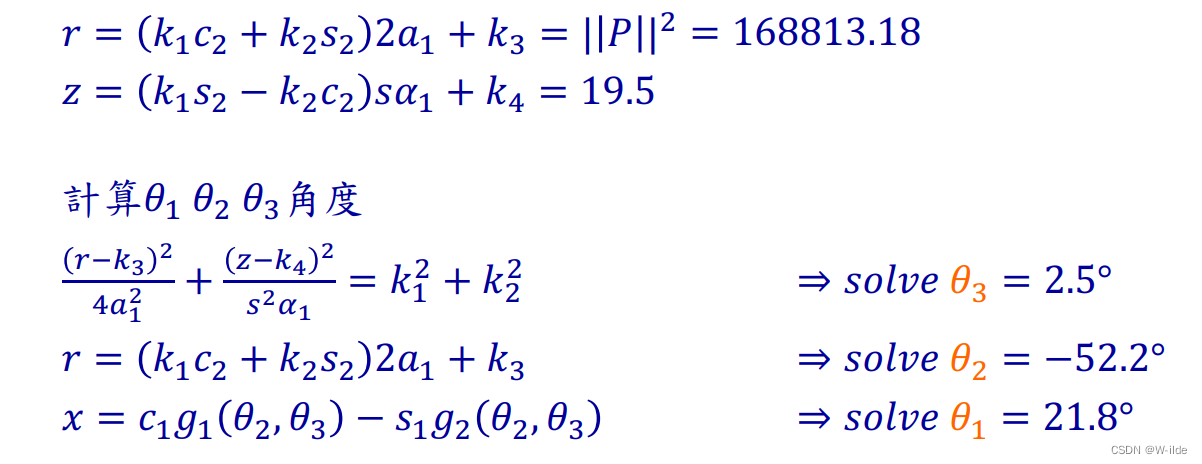
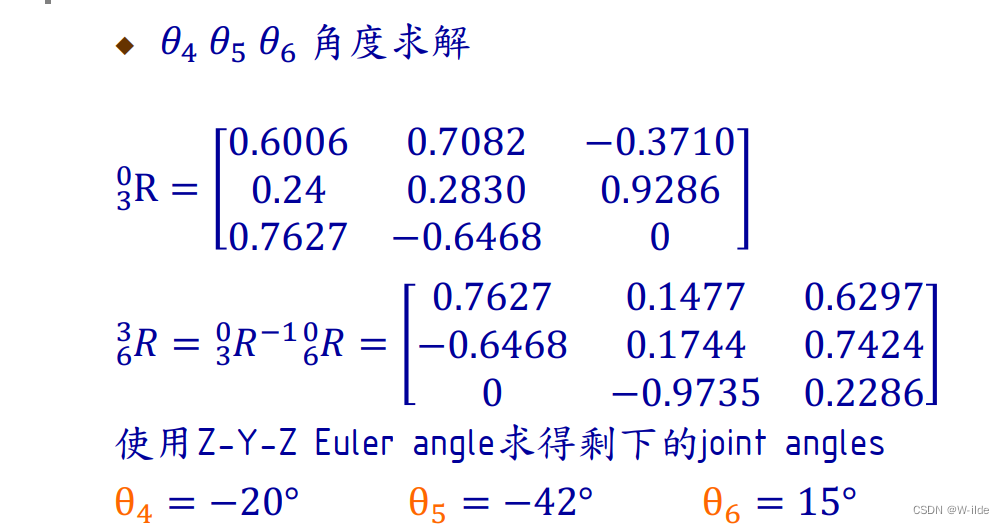
总结
以上就是今天要讲的内容,本文仅仅简单介绍了 多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法的学习记录03——机械臂运动学逆解,而Matlab提供了大量能使我们快速便捷地处理数据的函数和方法。如有任何问题,可发邮件至layraliu@foxmail.com问询。
这篇关于多轴机械臂/正逆解/轨迹规划/机器人运动学/Matlab/DH法 学习记录03——机械臂运动学逆解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






