鲁棒线性模型估计(Robust linear model estimation)

本文主要是介绍鲁棒线性模型估计(Robust linear model estimation)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

鲁棒线性模型估计

1.RANSAC算法
- 1.1 算法的基本原理
- 1.2 迭代次数N的计算
- 1.3 参考代码
参考文献

当数据中出现较多异常点时，常用的线性回归OLS会因为这些异常点的存在无法正确估计线性模型的参数：
$\qquad \qquad W=(X^TX)^{-1}X^TY$

此时就需要寻找更鲁棒的方法过滤掉异常点，以获得更准确的模型预测参数。

1.RANSAC算法

1.1 算法的基本原理

RANSAC（random sample consensus，随机抽样一致算法)基本原理如下：
———————————————————————————————————————
变量
$\quad N$ ：迭代次数；
$\quad s$ ：每次迭代过程，用于估计模型参数最小的样本点数量；
$\quad \tau$ ：每次迭代过程，用于辨别正常点和异常点的阈值；
$\quad d$ ：每次迭代过程，对辨别到的正常点进行线性拟合所需的最小个数;
$\quad bestErr$ ：最佳误差，用于判断是否更新模型参数，初始值可设为无穷大值。
$\quad bestModel$ ：最佳模型。

算法

进行N次迭代：

随机抽取 $s$ 个样本数据，对这 $s$ 个数据进行线性拟合，得到初始模型 $model_1$ ；
使用 $model_1$ ，对 $s$ 个数据中各数据的自变量进行预测，获得对应的 $\hat{y}$ ，计算误差值 $(y-\hat{y})^2$ 。如果误差值小于 $\tau$ ，则为正常点，否则为异常点；
若正常点个数小于 $d$ ，直接进入下一次循环；
使用正常点进行线性拟合，获取模型 $model_2$ ；
对判断出的正常点求均方差 $Err=\cfrac{1}{n}\sum(y-\hat{y})^2$ ， $n$ 为正常点的个数；
如果 $E rr < b es tE rr$ ，那么设置 $b es tE rr = E rr$ ，同时设置 $bestModel=model_2$ 。
————————————————————————————————————————

1.2 迭代次数N的计算

迭代次数 $N$ 的计算满足下式：

$\qquad 1-(1-(1-e)^s)^N=p$

其中：
$\qquad e$ 为数据中异常点的概率；
$\qquad p$ 为 $N$ 次迭代过程中，至少存在一次采样数据全为正常点的期望概率，如设置为0.99。

因此有：
$\qquad N=\cfrac{\log(1-p)}{\log(1-(1-e)^s)}$

1.3 参考代码

代码来源于https://en.wikipedia.org/wiki/Random_sample_consensus：

from copy import copy
import numpy as np
from numpy.random import default_rng
rng = default_rng()class RANSAC:def __init__(self, n=10, k=100, t=0.05, d=10, model=None, loss=None, metric=None):self.n = n              # `n`: Minimum number of data points to estimate parametersself.k = k              # `k`: Maximum iterations allowedself.t = t              # `t`: Threshold value to determine if points are fit wellself.d = d              # `d`: Number of close data points required to assert model fits wellself.model = model      # `model`: class implementing `fit` and `predict`self.loss = loss        # `loss`: function of `y_true` and `y_pred` that returns a vectorself.metric = metric    # `metric`: function of `y_true` and `y_pred` and returns a floatself.best_fit = Noneself.best_error = np.infdef fit(self, X, y):for _ in range(self.k):ids = rng.permutation(X.shape[0])maybe_inliers = ids[: self.n]maybe_model = copy(self.model).fit(X[maybe_inliers], y[maybe_inliers])thresholded = (self.loss(y[ids][self.n :], maybe_model.predict(X[ids][self.n :]))< self.t)inlier_ids = ids[self.n :][np.flatnonzero(thresholded).flatten()]if inlier_ids.size > self.d:inlier_points = np.hstack([maybe_inliers, inlier_ids])better_model = copy(self.model).fit(X[inlier_points], y[inlier_points])this_error = self.metric(y[inlier_points], better_model.predict(X[inlier_points]))if this_error < self.best_error:self.best_error = this_errorself.best_fit = better_modelreturn selfdef predict(self, X):return self.best_fit.predict(X)def square_error_loss(y_true, y_pred):return (y_true - y_pred) ** 2def mean_square_error(y_true, y_pred):return np.sum(square_error_loss(y_true, y_pred)) / y_true.shape[0]class LinearRegressor:def __init__(self):self.params = Nonedef fit(self, X: np.ndarray, y: np.ndarray):r, _ = X.shapeX = np.hstack([np.ones((r, 1)), X])self.params = np.linalg.inv(X.T @ X) @ X.T @ yreturn selfdef predict(self, X: np.ndarray):r, _ = X.shapeX = np.hstack([np.ones((r, 1)), X])return X @ self.paramsif __name__ == "__main__":regressor = RANSAC(model=LinearRegressor(), loss=square_error_loss, metric=mean_square_error)X = np.array([-0.848,-0.800,-0.704,-0.632,-0.488,-0.472,-0.368,-0.336,-0.280,-0.200,-0.00800,-0.0840,0.0240,0.100,0.124,0.148,0.232,0.236,0.324,0.356,0.368,0.440,0.512,0.548,0.660,0.640,0.712,0.752,0.776,0.880,0.920,0.944,-0.108,-0.168,-0.720,-0.784,-0.224,-0.604,-0.740,-0.0440,0.388,-0.0200,0.752,0.416,-0.0800,-0.348,0.988,0.776,0.680,0.880,-0.816,-0.424,-0.932,0.272,-0.556,-0.568,-0.600,-0.716,-0.796,-0.880,-0.972,-0.916,0.816,0.892,0.956,0.980,0.988,0.992,0.00400]).reshape(-1,1)y = np.array([-0.917,-0.833,-0.801,-0.665,-0.605,-0.545,-0.509,-0.433,-0.397,-0.281,-0.205,-0.169,-0.0531,-0.0651,0.0349,0.0829,0.0589,0.175,0.179,0.191,0.259,0.287,0.359,0.395,0.483,0.539,0.543,0.603,0.667,0.679,0.751,0.803,-0.265,-0.341,0.111,-0.113,0.547,0.791,0.551,0.347,0.975,0.943,-0.249,-0.769,-0.625,-0.861,-0.749,-0.945,-0.493,0.163,-0.469,0.0669,0.891,0.623,-0.609,-0.677,-0.721,-0.745,-0.885,-0.897,-0.969,-0.949,0.707,0.783,0.859,0.979,0.811,0.891,-0.137]).reshape(-1,1)regressor.fit(X, y)import matplotlib.pyplot as pltfig, ax = plt.subplots(1, 1)ax.set_box_aspect(1)plt.scatter(X, y)line = np.linspace(-1, 1, num=100).reshape(-1, 1)plt.plot(line, regressor.predict(line), c="peru")plt.show(block=True)

结果如下：
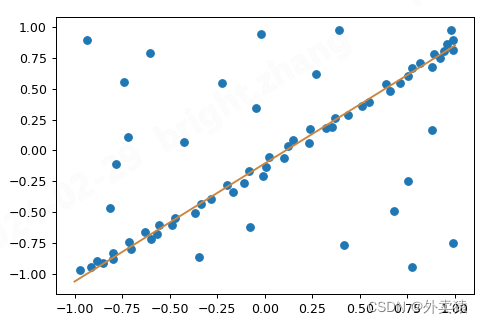
在这里插入图片描述

参考文献

[1] https://www.cse.psu.edu/~rtc12/CSE486/lecture15.pdf
[2] https://en.wikipedia.org/wiki/Random_sample_consensus
[3] Overview of the RANSAC Algorithm
[4] https://scikit-learn.org/stable/auto_examples/linear_model/plot_ransac.html

这篇关于鲁棒线性模型估计(Robust linear model estimation)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！