本文主要是介绍间接调制和带通采样!!(非奈奎斯特采样定理),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 直接变频
前面讲解数字调制原理时,直接利用IQ调制将基带信号变换为频带信号,这种频率变换一般被称为直接上变频;解调时,直接利用IQ解调,将频带信号变换回基带信号,这种频率变换一般被称为直接下变频。直接上变频和直接下变频统称直接变频。
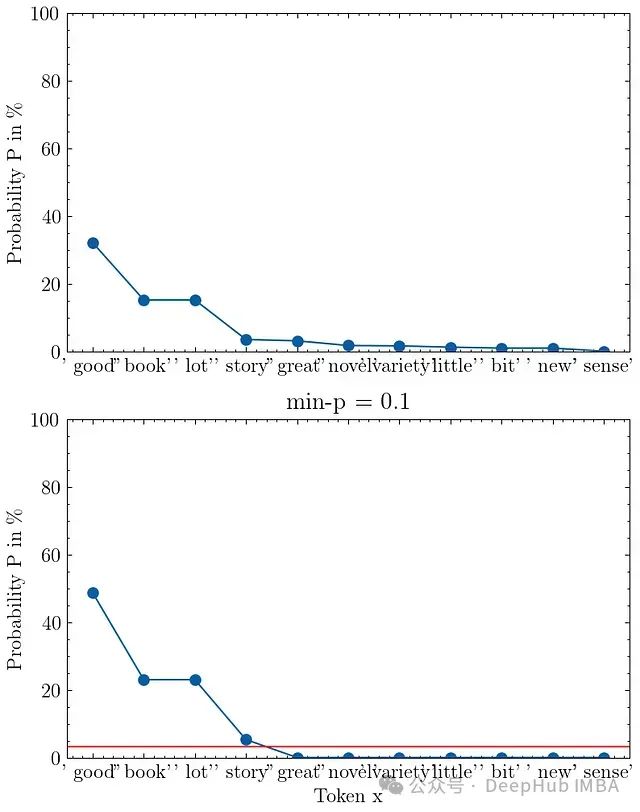
在采用直接变频的情况下,假定基带IQ信号的波形如下图所示。

则射频信号的波形如下图所示。
2. 间接变频
通信系统中,考虑到实现难度等因素,有时候不将基带信号直接变换为射频信号,或者将射频信号直接变换为基带信号,而是先将基带信号变换到中频,再从中频变换到射频,这被称为间接上变频;反之:先将射频信号变换到中频,再从中频变换到基带,这被称为间接下变频。间接上变频和间接下变频统称间接变频。
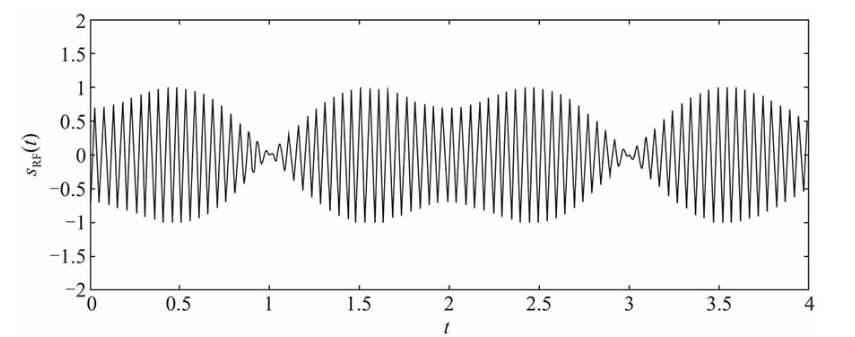
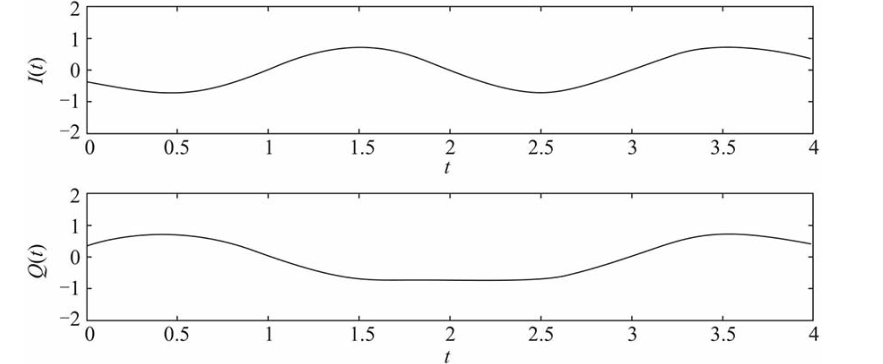
在采用间接变频的情况下,假定基带IQ信号的波形如下图所示。
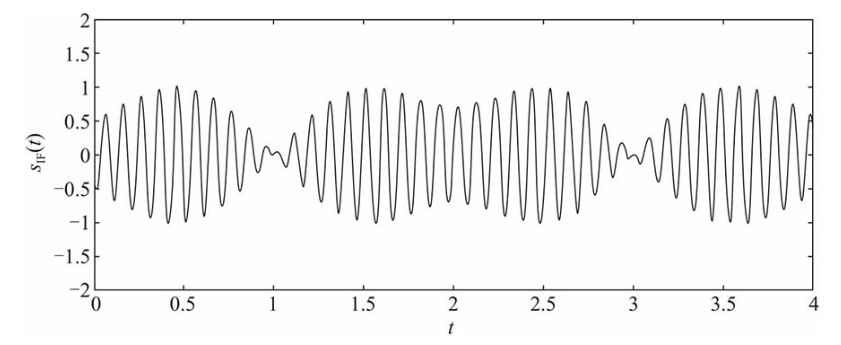
则中频信号的波形如下图所示
射频信号的波形如下图所示 。
2.1 间接上变频
将基带信号调制到中频载波上,再将中频载波变换为射频载波的过程,就是间接上变频,如下图所示。

a 基带变换到中频
这个变换过程实质上就是IQ调制的过程,只不过载波的频率是中频而已。
b 中频变换到射频
通过滤波器滤除低频成分:
2.2 间接下变频
将射频载波变换为中频载波,再从中频信号解调出基带信号的过程,就是间接下变频,如下图所示。
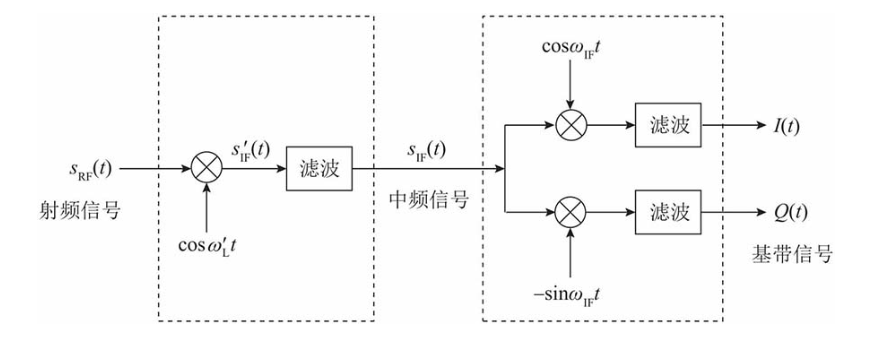
a 射频变换到中频
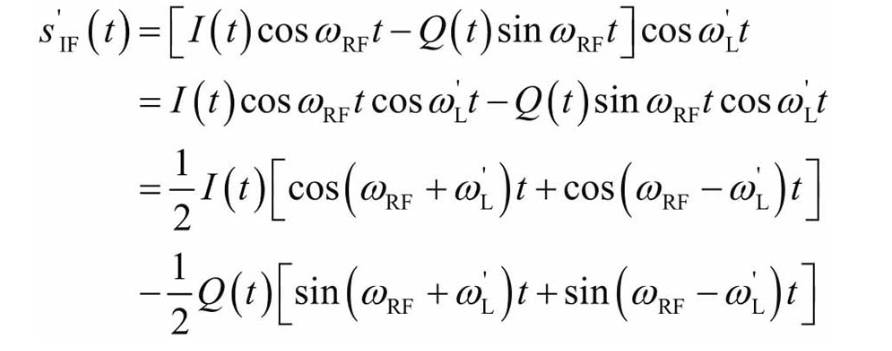
通过滤波器滤除高频成分:
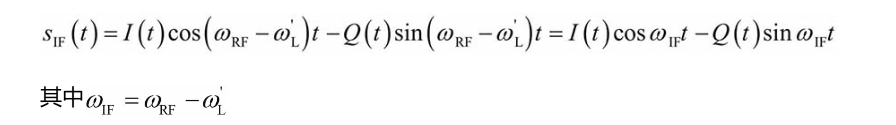
这个过程实质上就是一个混频的过程,将载波频率由射频变换为中频。
b 中频变换到基带
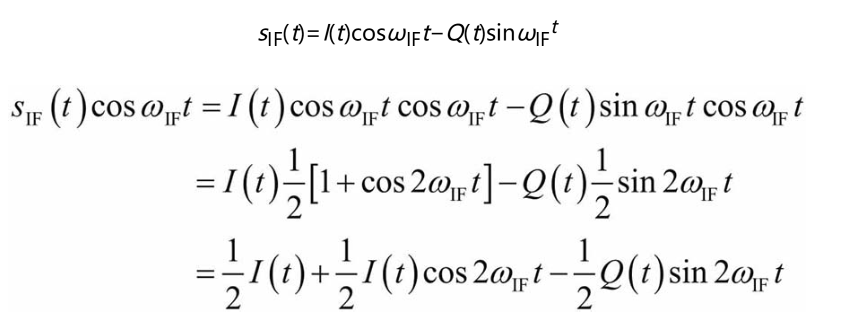

通过滤波器滤除高频成分,即可得到I(t),Q(t)。
这个过程实质上就是IQ解调的过程,只不过已调信号的载波频率是中频而已。
3. 数字变频
一般基带信号都是数字信号,中频处理也是数字化的,因此基带和中频之间的上变频和下变频一般都是通过数字信号处理来实现。
3.1 数字上变频
DUC:Digital Up Converter,数字上变频器,通过数字信号处理实现上变频功能,如下图所示。

3.2 数字下变频
DDC:Digital Down Converter,数字下变频器,通过数字信号处理实现下变频功能,如下图所示。

4. 带通采样
模拟下变频得到的模拟中频信号,需要进行模数转换,才能进行后续的数字信号处理。
模数转换涉及采样。前面所讲的奈奎斯特采样定理(也被称为低通信号采样定理)是针对基带信号讲的,而这里的采样是针对带通信号讲的。
4.1 什么是带通信号
基带信号经过载波调制后得到的已调信号被称为频带信号,也称为带通信号。直接变频得到的射频信号、间接变频得到的中频信号和射频信号都是带通信号。
基带信号经过载波调制后得到的已调信号被称为频带信号,也称为带通信号。直接变频得到的射频信号、间接变频得到的中频信号和射频信号都是带通信号。如果根据前面讲的采样定理,以大于2倍最高频率的采样频率对带通信号进行采样,肯定可以从抽样信号中恢复出带通信号,这是毫无疑问的。但由于一般带通信号的载波频率都比较高,动辄几十、几百MHz,如果使用大于2倍最高频率的采样频率,对ADC的处理能力要求很高。按目前ADC器件的处理能力,能达到几百MSPS(Million Samples Per Second)采样频率的ADC就算是处理能力比较强的了,而且支持如此高采样频率的ADC价格很高。能不能用低一些的采样频率对带通信号进行采样呢?这就引出了带通信号采样定理。
4.2 带通信号采样定理
中心频率为f0、带宽为B的带通信号,其高、低截止频率分别为:fH=f0+B/2和fL=f0-B/2,其频谱如下图所示。
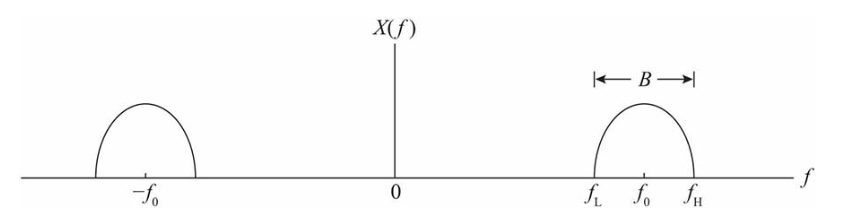

这就是带通采样定理。
4.3 带通采样定理的推导过程
虽然带通采样定理的结论看起来不像低通信号采样定理那样简洁,但是它们的推导方法类似,都是从避免抽样信号频谱发生混叠的角度推导出来的。唯一需要注意的是:对带通信号进行采样,相当于对其频谱进行周期性拓展,在对频谱进行周期性拓展时,正频率部分和负频率部分要一起拓展。
假定带通信号的频谱如下图所示,其截止频率:fL=2B,fH=3B。

以采样频率fs对该信号进行采样时,频谱将会以fs为间隔进行周期性拓展。
(1)当采样频率很高时,很明显,周期拓展的频谱之间不会发生混叠,如下图所示。
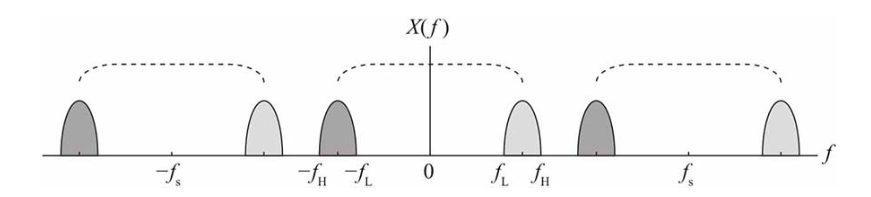
减小fs,右边的频谱将向左挪,左边的频谱将向右挪,直至和原频谱刚好挨上为止,此时fs=2fH,如下图所示。
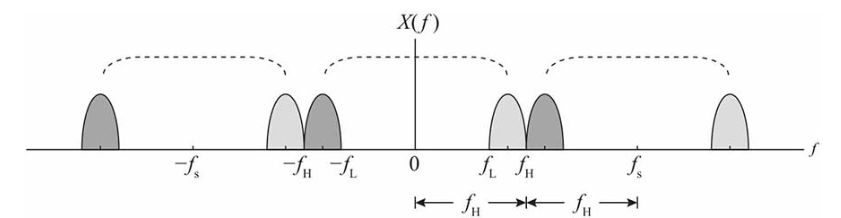
如果继续减小fs,频谱就会发生混叠了,必须跳过一段频率,到达如下图所示位置才不会发生混叠,此时刚好fs=2fL。
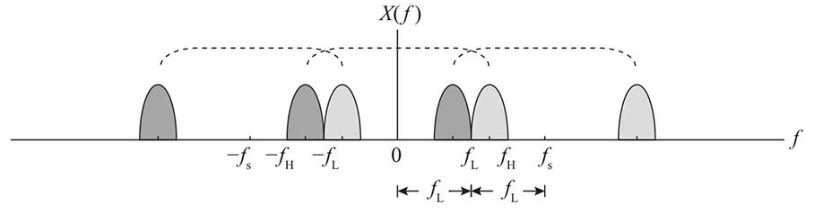
继续减小fs,右边的频谱将向左挪,左边的频谱将向右挪,直至频谱刚好挨上为止,此时fs=fH,如下图所示。
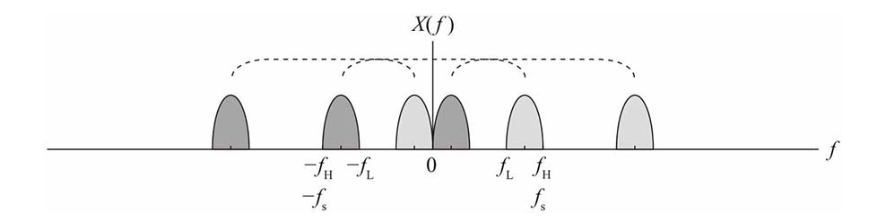
如果继续减小fs,频谱就会发生混叠了,必须跳过一段频率,到达如下图所示位置才不会发生混叠,此时刚好fs=fL=2B。
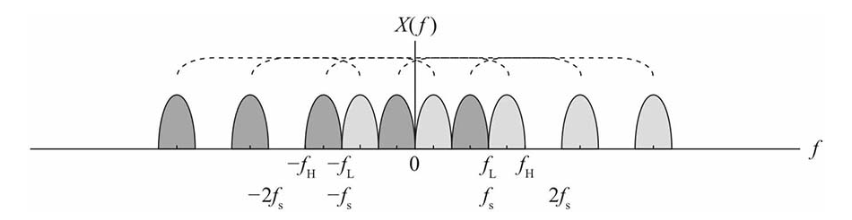
注意:这时候fs不能再进一步减小了,否则就发生混叠了。

下面对比一下带通采样定理给出的结论。

根据带通采样定理,以满足下面条件的采样频率fs对带通信号进行采样,都可以将带通信号无失真地恢复出来:
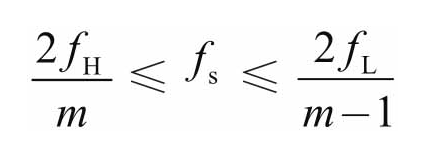
满足条件的采样频率fs由高到低被分成了3个部分:

对比一下前面推导得到的结论,可以发现二者是完全相同的。
4.4 图解满足带通采样定理的采样频率
为了更清楚地认识带通采样定理中采样频率fs和最高信号频率fH的关系,我们以fH为横轴,以fs为纵轴,把满足带通采样定理的采样频率画在一张图中,如下图所示。
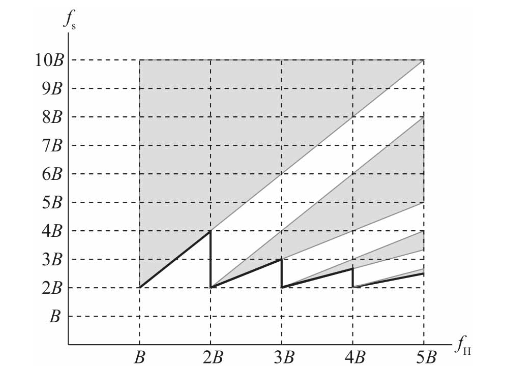
图中灰色区域表示满足带通采样定理的采样频率范围。
还是以fH=3B为例,采样频率范围为:fs=2B,3B≤fs≤4B,fs≥6B。
黑线所示为满足带通采样定理的最低采样频率:

随着带通信号最高频率的增大,黑色斜线的斜率越来越小,当带通信号的最高频率远远大于信号带宽时,黑色斜线将趋近于一条水平线,只要以略大于2倍信号带宽的采样频率对带通信号采样即可,如下图所示。
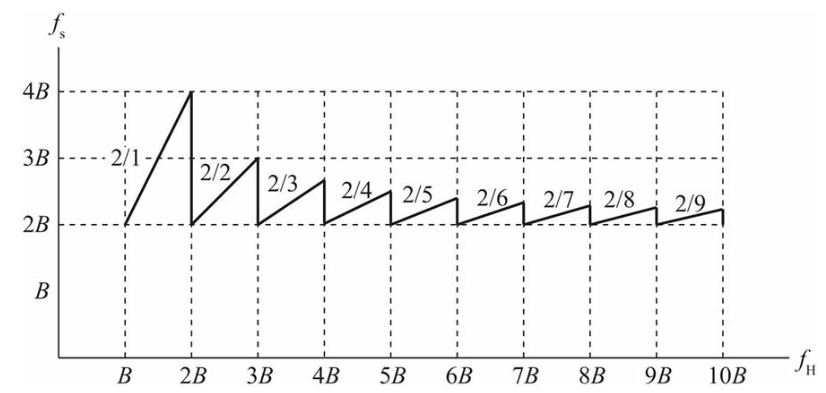
当带通信号的最高频率(fH)正好是信号带宽(B)的整数倍时,满足带通采样定理的最低采样频率正好是带宽的2倍。其他情况采样频率都大于信号带宽的2倍。
为了用最低的采样频率(fs=2B)对带通信号进行采样,在设计带通信号时,一般将带通信号的最高频率设计成带宽的整数倍(fH=kB),如下图所示。
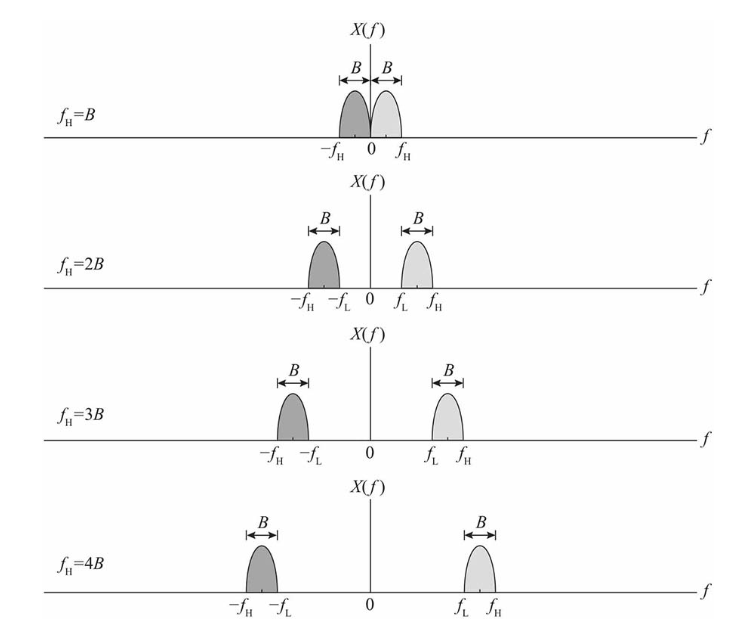
4.5 带通采样定理和奈奎斯特采样定理的关系
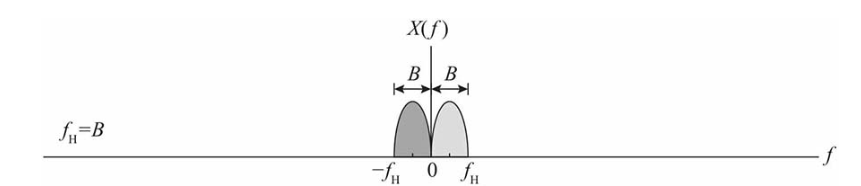
带通信号采样定理中,令fH=B,则mmax=1。对应的带通信号频谱如下图所示。这种信号一般被称为低通信号。
根据带通信号采样定理,采样频率fs应满足:
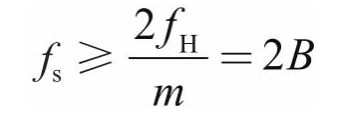
这就是奈奎斯特采样定理。
这篇关于间接调制和带通采样!!(非奈奎斯特采样定理)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!