重复采样魔法：用更多样本击败单次尝试的最强模型

2024-09-07 15:44
文章标签 模型 尝试 重复 最强 采样 魔法 多样 单次 击败

本文主要是介绍重复采样魔法：用更多样本击败单次尝试的最强模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

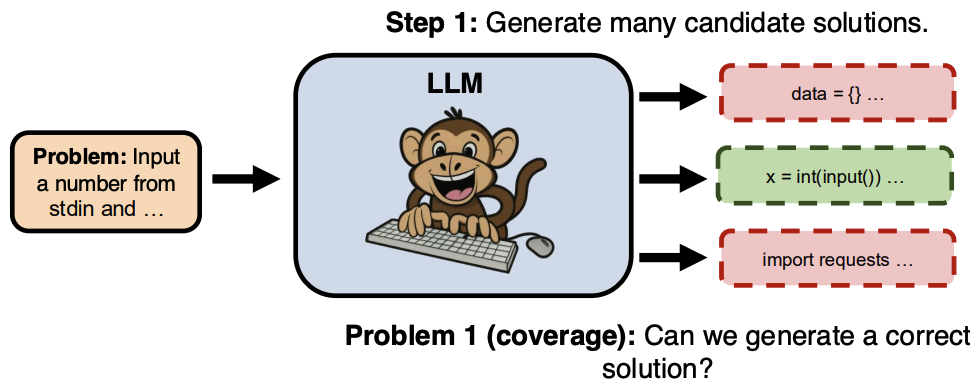
d8ca7864abf7597b7be731a1e867abdf.png

这篇文章探讨了通过增加生成样本的数量来扩展大型语言模型（LLMs）在推理任务中的表现。

研究发现，重复采样可以显著提高模型的覆盖率，特别是在具有自动验证工具的任务中。研究还发现，覆盖率与样本数量之间的关系可以用指数幂律建模，揭示了推理时间的扩展规律。尽管多数投票和奖励模型在样本数量增加时趋于饱和，但在没有自动验证工具的任务中，识别正确样本仍然是一个重要的研究方向。

总体而言，重复采样提供了一种有效的方法来增强较弱模型的能力，并在某些情况下比使用更强大、更昂贵的模型更具成本效益。

论文：Large Language Monkeys: Scaling Inference Compute with Repeated Sampling
链接：https://arxiv.org/pdf/2407.21787

研究背景

  1. 研究问题：这篇文章探讨了如何通过增加生成样本的数量来扩展推理计算，从而提高大型语言模型（LLMs）在推理任务中的表现。具体来说，研究了重复采样作为一种扩展推理计算的方法，以提高模型的覆盖率和精度。

  2. 研究难点：该问题的研究难点包括：如何在有限的预算内提高覆盖率，如何在不具备自动验证工具的任务中识别正确的样本，以及如何在性能和成本之间找到平衡。

  3. 相关工作：相关研究表明，通过扩展训练计算量可以显著提高LLMs的能力。然而，在推理阶段，用户和开发者通常限制模型只进行一次尝试。已有工作表明，重复采样在数学、编程和拼图解决设置中可以提高性能。

研究方法

这篇论文提出了通过重复采样来扩展推理计算，以提高LLMs的性能。具体来说，

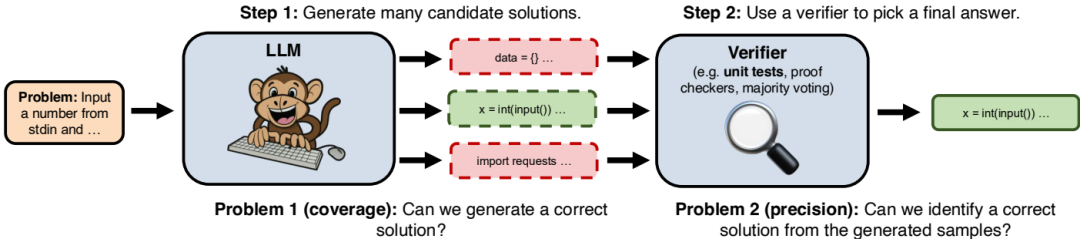
  1. 重复采样过程：首先，通过从LLM中采样生成许多候选解决方案。然后，使用领域特定的验证器（例如代码的单位测试）从生成的样本中选择最终答案。bb39dc7d7517f2239c3694362ec36d9c.png

  2. 覆盖率和精度：重复采样的有效性取决于两个关键属性：覆盖率和精度。覆盖率是指通过生成样本能够解决问题的比例；精度是指在需要从多个样本中选择最终答案的情况下，能否识别出正确样本。

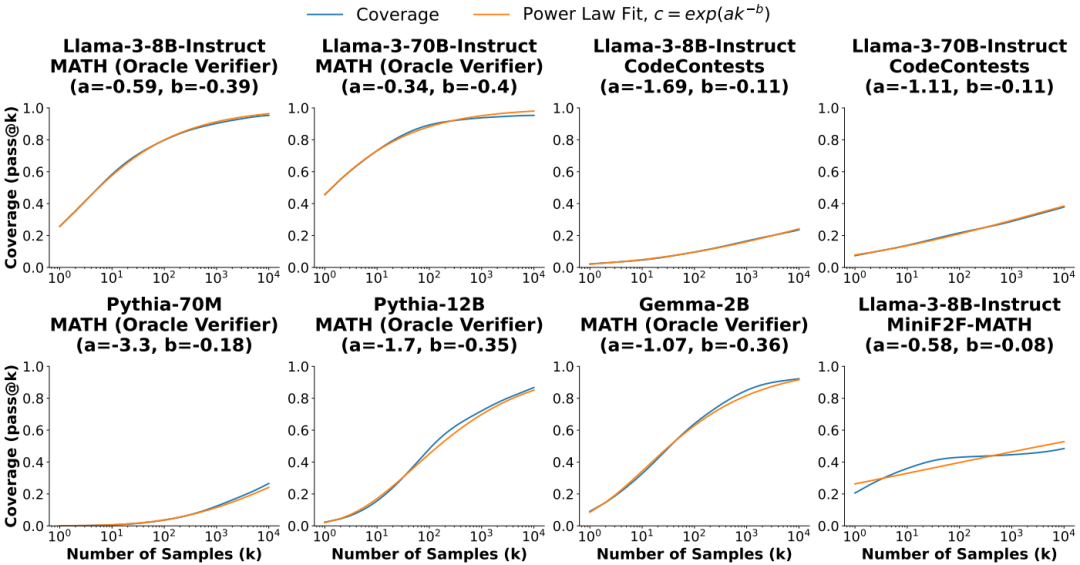
  3. 覆盖率的建模：研究发现，覆盖率与样本数量之间的关系通常可以用指数幂律建模，即：

其中，a 和 b 是拟合的模型参数。通过对数变换，最终的模型为：

这表明推理时间的扩展规律可能存在。

cff7dfff20d3e3343e7f7f45db5ee5ce.png

实验设计

  1. 任务和模型：实验涵盖了五个任务：GSM8K、MATH、MiniF2F-MATH、CodeContests和SWE-bench Lite。使用了多个模型家族，包括Llama 3、Gemma和Pythia。

  2. 数据集：GSM8K和MATH是数学单词问题数据集，MiniF2F-MATH是形式化数学问题的数据集，CodeContests是编程竞赛问题数据集，SWE-bench Lite是GitHub实际问题的数据集。

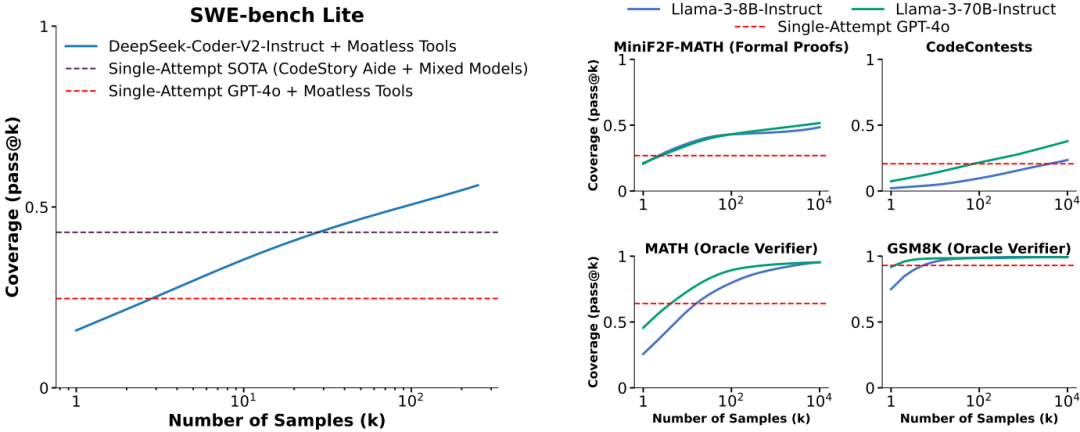
  3. 采样策略：在每个任务中，每个问题生成10,000个独立样本。对于SWE-bench Lite，由于所需的上下文长度超过了Llama 3模型的极限，使用了DeepSeek-V2-Coder-Instruct模型，并限制了每个问题的尝试次数为250次。

  4. 验证工具：在具有自动验证工具的任务中（如Lean证明检查和单元测试），直接使用这些工具来评估覆盖率。在没有自动验证工具的任务中（如GSM8K和MATH），使用多数投票和奖励模型来选择最终答案。

结果与分析

  1. 覆盖率提升：在所有任务中，随着样本数量的增加，覆盖率平滑提升。例如，在使用Gemma-2B模型解决CodeContests问题时，覆盖率从10,000次尝试的0.02%提高到7.1%。7f60a8031d1d6b24b865b7a0f94a2661.png

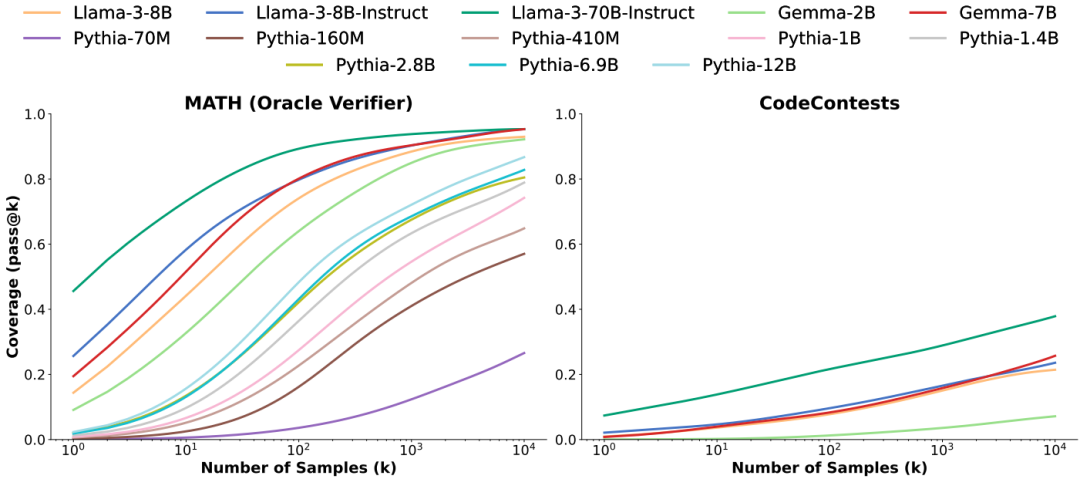
  2. 模型大小和家族的广泛适用性：重复采样在不同模型大小、家族和训练水平上均表现出覆盖率提升。较小的模型在应用重复采样时显示出更显著的覆盖率提升。e75081f31e2b7eb8a5053374d7cfbdcf.png

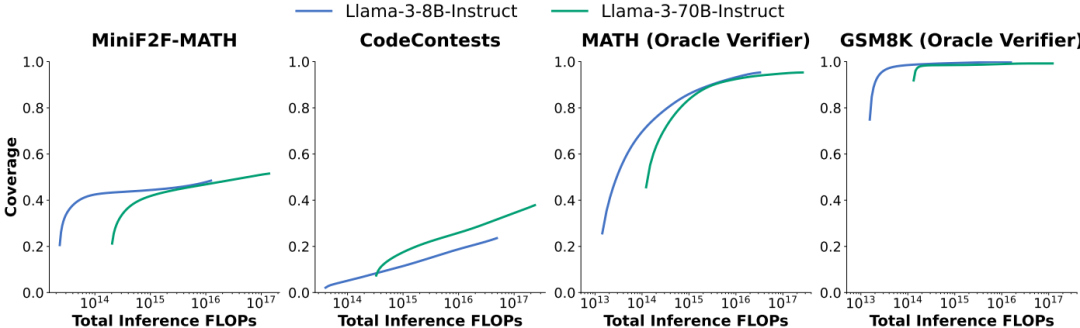
  3. 性能和成本平衡：通过重复采样，较弱的模型可以在成本和性能之间取得更好的平衡。例如，使用DeepSeek-V2-Coder-Instruct模型进行SWE-bench Lite问题的重复采样，比使用GPT-4o或Claude 3.5 Sonnet模型单次尝试更经济高效。be24e2477b14009a7cd96004cb84e383.png

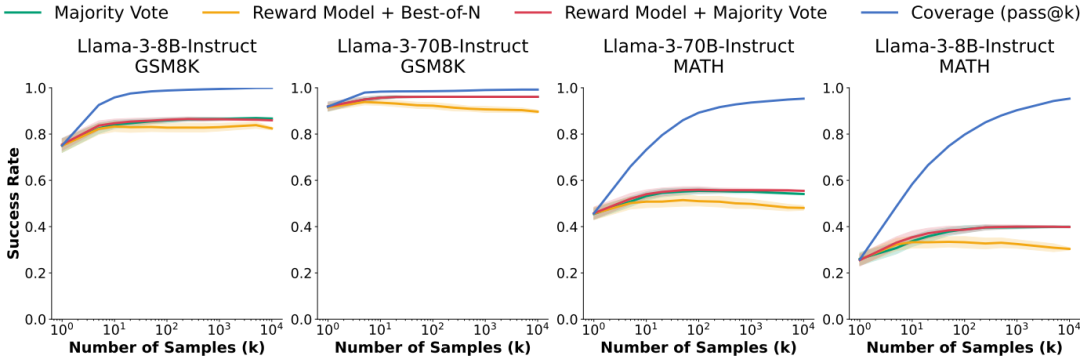
  4. 验证方法的局限性：在GSM8K和MATH任务中，多数投票和奖励模型在样本数量超过100后趋于饱和，未能完全随样本预算扩展。5d6c38b4056382098e1e6904e43992e8.png

总体结论

这篇论文展示了通过重复采样扩展推理计算可以显著提高LLMs的性能，特别是在具有自动验证工具的任务中。研究结果表明，覆盖率与样本数量之间的关系可以用指数幂律建模，不同模型家族内的覆盖率曲线具有相似的形状。此外，尽管多数投票和奖励模型在样本数量增加时趋于饱和，但在没有自动验证工具的任务中，识别正确样本仍然是一个重要的研究方向。总体而言，重复采样提供了一种有效的方法来增强较弱模型的能力，并在某些情况下比使用更强大、更昂贵的模型更具成本效益。

AI辅助人工完成。

备注：昵称-学校/公司-方向/会议(eg.ACL)，进入技术/投稿群

45b279bb5416c2bdce25927950708827.png

id：DLNLPer，记得备注呦

这篇关于重复采样魔法：用更多样本击败单次尝试的最强模型的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1145473。

相关文章

大模型研发全揭秘：客服工单数据标注的完整攻略

大模型研发全揭秘：客服工单数据标注的完整攻略

在人工智能（AI）领域，数据标注是模型训练过程中至关重要的一步。无论你是新手还是有经验的从业者，掌握数据标注的技术细节和常见问题的解决方案都能为你的AI项目增添不少价值。在电信运营商的客服系统中，工单数据是客户问题和解决方案的重要记录。通过对这些工单数据进行有效标注，不仅能够帮助提升客服自动化系统的智能化水平，还能优化客户服务流程，提高客户满意度。本文将详细介绍如何在电信运营商客服工单的背景下进行
阅读更多...
Andrej Karpathy最新采访：认知核心模型10亿参数就够了，AI会打破教育不公的僵局

Andrej Karpathy最新采访：认知核心模型10亿参数就够了，AI会打破教育不公的僵局

夕小瑶科技说 原创  作者 | 海野 AI圈子的红人，AI大神Andrej Karpathy，曾是OpenAI联合创始人之一，特斯拉AI总监。上一次的动态是官宣创办一家名为 Eureka Labs 的人工智能+教育公司 ，宣布将长期致力于AI原生教育。 近日，Andrej Karpathy接受了No Priors（投资博客）的采访，与硅谷知名投资人 Sara Guo 和 Elad G
阅读更多...
poj2406（连续重复子串）

poj2406（连续重复子串）

题意:判断串s是不是str^n，求str的最大长度。 解题思路：kmp可解，后缀数组的倍增算法超时。next[i]表示在第i位匹配失败后，自动跳转到next[i]，所以1到next[n]这个串 等于 n-next[n]+1到n这个串。 代码如下； #include<iostream>#include<algorithm>#include<stdio.h>#include<math.
阅读更多...
poj3261（可重复k次的最长子串）

poj3261（可重复k次的最长子串）

题意：可重复k次的最长子串 解题思路：求所有区间[x,x+k-1]中的最小值的最大值。求sa时间复杂度Nlog(N),求最值时间复杂度N*N，但实际复杂度很低。题目数据也比较水，不然估计过不了。 代码入下： #include<iostream>#include<algorithm>#include<stdio.h>#include<math.h>#include<cstring
阅读更多...
Retrieval-based-Voice-Conversion-WebUI模型构建指南

Retrieval-based-Voice-Conversion-WebUI模型构建指南

一、模型介绍 Retrieval-based-Voice-Conversion-WebUI（简称 RVC）模型是一个基于 VITS（Variational Inference with adversarial learning for end-to-end Text-to-Speech）的简单易用的语音转换框架。 具有以下特点 简单易用：RVC 模型通过简单易用的网页界面，使得用户无需深入了
阅读更多...
透彻！驯服大型语言模型（LLMs）的五种方法，及具体方法选择思路

透彻！驯服大型语言模型（LLMs）的五种方法，及具体方法选择思路

引言 随着时间的发展，大型语言模型不再停留在演示阶段而是逐步面向生产系统的应用，随着人们期望的不断增加，目标也发生了巨大的变化。在短短的几个月的时间里，人们对大模型的认识已经从对其zero-shot能力感到惊讶，转变为考虑改进模型质量、提高模型可用性。 「大语言模型(LLMs)其实就是利用高容量的模型架构（例如Transformer）对海量的、多种多样的数据分布进行建模得到，它包含了大量的先验
阅读更多...
图神经网络模型介绍（1）

图神经网络模型介绍（1）

我们将图神经网络分为基于谱域的模型和基于空域的模型，并按照发展顺序详解每个类别中的重要模型。 1.1基于谱域的图神经网络         谱域上的图卷积在图学习迈向深度学习的发展历程中起到了关键的作用。本节主要介绍三个具有代表性的谱域图神经网络：谱图卷积网络、切比雪夫网络和图卷积网络。 （1）谱图卷积网络 卷积定理：函数卷积的傅里叶变换是函数傅里叶变换的乘积，即F{f*g}
阅读更多...
秋招最新大模型算法面试，熬夜都要肝完它

秋招最新大模型算法面试，熬夜都要肝完它

💥大家在面试大模型LLM这个板块的时候，不知道面试完会不会复盘、总结，做笔记的习惯，这份大模型算法岗面试八股笔记也帮助不少人拿到过offer ✨对于面试大模型算法工程师会有一定的帮助，都附有完整答案，熬夜也要看完，祝大家一臂之力 这份《大模型算法工程师面试题》已经上传CSDN，还有完整版的大模型 AI 学习资料，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费
阅读更多...
【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂 关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】 嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。 正如翻译机将一种语言
阅读更多...
AI Toolkit + H100 GPU，一小时内微调最新热门文生图模型 FLUX

AI Toolkit + H100 GPU，一小时内微调最新热门文生图模型 FLUX

上个月，FLUX 席卷了互联网，这并非没有原因。他们声称优于 DALLE 3、Ideogram 和 Stable Diffusion 3 等模型，而这一点已被证明是有依据的。随着越来越多的流行图像生成工具（如 Stable Diffusion Web UI Forge 和 ComyUI）开始支持这些模型，FLUX 在 Stable Diffusion 领域的扩展将会持续下去。 自 FLU
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2