A Gift from Knowledge Distillation: Fast Optimization,Network Minimization and Transfer Learning论文初读

2024-02-13 14:40
文章标签 论文 network learning optimization transfer fast knowledge distillation gift 初读 minimization

本文主要是介绍A Gift from Knowledge Distillation: Fast Optimization,Network Minimization and Transfer Learning论文初读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

摘要

引言

相关工作

  知识迁移

  快速优化

  迁移学习

方法

  提出观点

  数学表达式

  FSP Matrix的损失

  学习步骤

实验

  快速优化

  性能的提升

  迁移学习

结论

摘要

提出了将蒸馏的知识看作成一种解决问题的流，它是在不同层之间的feature通过内积计算得到的

这个方法有三个好处：

  student网络可以学的更快

  student网络可以超过teacher网路的性能

  可以适用于迁移学习（teacher和student属于不同的任务）

引言

  • 之前的工作

KD

Fitnets（hint）

  • 本文的创新点

将知识看作如何解决问题的流，所以将要蒸馏知识看作解决问题的流

流被定义为在两个不同层上的features上的关系

Gram matrix是通过计算特征间的内积得到的，可以表示输入图像的纹理信息，本文也是通过计算Gram matrix来得到流，不同点在于原本的Gram matrix是计算一个层的特征间的内积，而本文是结算不同层特征间的内积

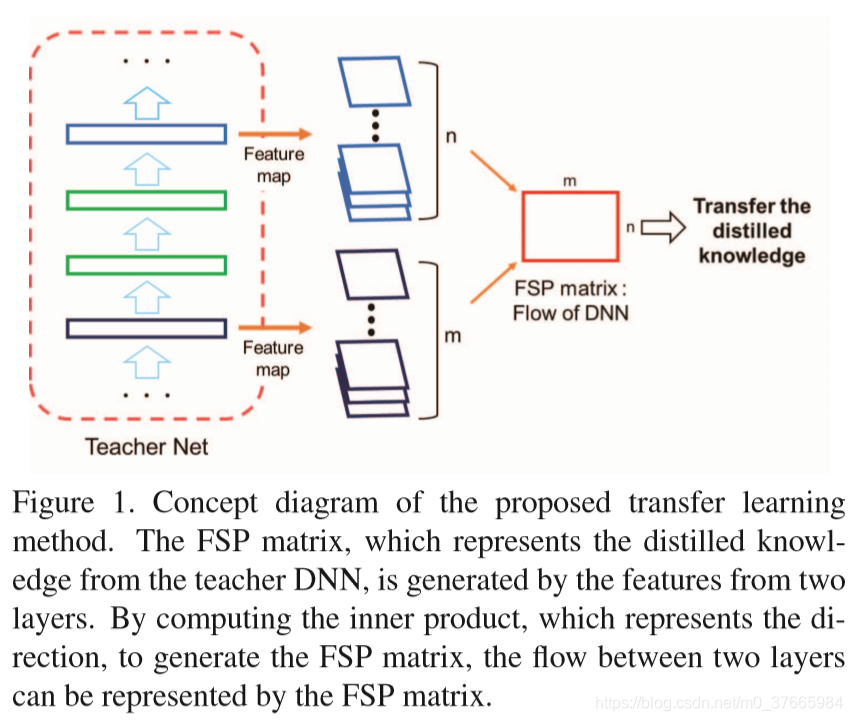
Figure1是计算FSP的概念图，FSP就是flow of solution procedure

  • 本文的贡献

提出了一种好的知识蒸馏的方法

这种方法对快速优化有帮助

这种方法可以显著提升student网络的性能

这种方法适用于迁移学习

相关工作

  知识迁移

KD

Fitnets

Net2Net根据teacher网络的参数，用一种函数保留的迁移方式初始化student网络的参数

  快速优化

Gaussian noise初始化

Xavier初始化

还有一些初始化方法

优化的新方法

  迁移学习

加载训练好的参数，微调

方法

  提出观点

将输入和输出看作是问题和答案，中间层看作是解决问题的一个步骤，按照Fitnets的思路，会学习中间这个步骤，然而解决这个问题可以有很多路径，中间这个步骤的状态不一定是一种，所以Fitnets给了太多的限制，作者提出学习输入和输出的关系，而不是直接学习中间的步骤的状态

  数学表达式

  • 表达式

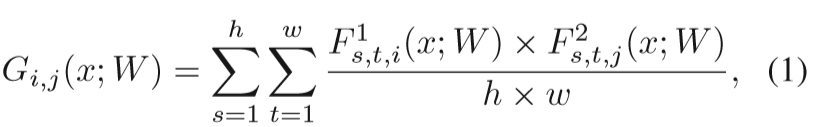
F1，F2是学生网络中两个不同层的特征

i，j表示F1和F2的通道号

这个式子其实就是不同通道的特征的相互内积

  • 计算G的位置

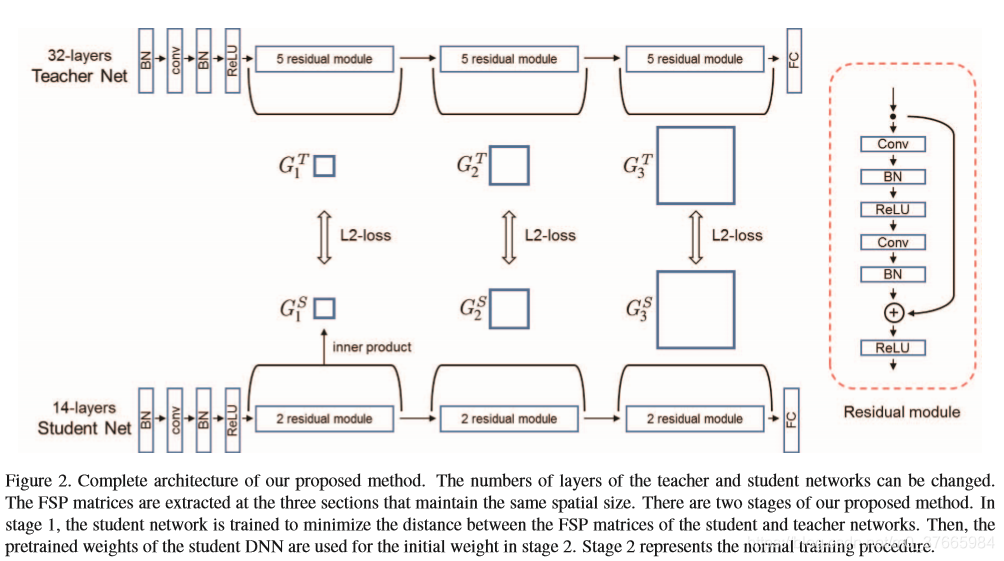
  FSP Matrix的损失

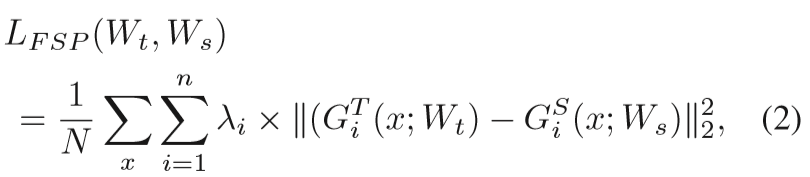
n代表在student中选择的层对数

N表示样本数量

T，S分别代表teacher和student

本论文的lamda对于所有的层对相同

  学习步骤

实验

  快速优化

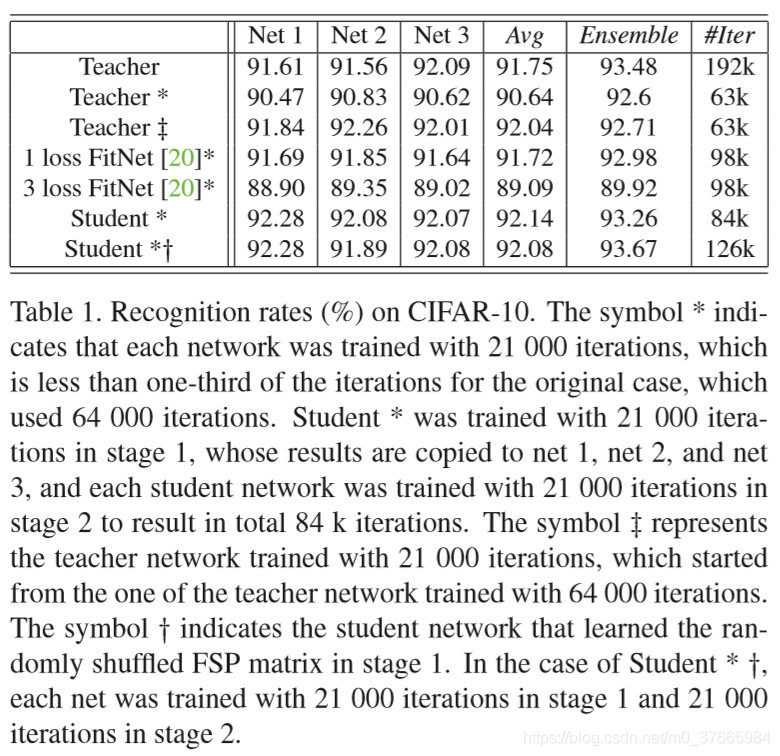
  • 关于Student与FitNet的分析

由于本文提出的结构是学习一种输入和输出的关系，本文是通过FSP实现的，所以多个FSP之间可以相对独立一些，整个模块可以解耦；

而对于FitNet，假设加入三个中间层，在第二个中间层和第三个中间层不好去学习，因为要想学习好他们，首先要保证前边的一层中间层学习好，所以FitNet这种直接用特征做监督信息的方式不能解耦多个loss层，这也是为什么三层FitNet没有一层FitNet效果好的原因；

FSP想比FitNet，赋予了网络更大的自由。如果student与teacher网络有相同的中间层，那么肯定有相同的FSP，但反过来确不成立，FSP的相同并不限制中间层的具体状态。

  • 关于加强多个Student的不相关性，从而提升集成模型的准确率

​​​​​​​Table1的倒数第二行：虽然student网络的单体能力已经超过了teacher网络，但是集成的student网络确没有集成的teacher的集成效果好，这是因为多个student网络的FSP矩阵是一致的，导致他们的相关性太大

Table1的倒数第一行：作者提出了将生成的FSP矩阵的行和列进行重新洗牌，得到新的几个FSP，用新的FSP训练student得到的集成效果要好。其实这相当于将生成FSP的两个不同层的特征的通道打乱而得出的FSP，本质上没有改变信息的内容。

  性能的提升

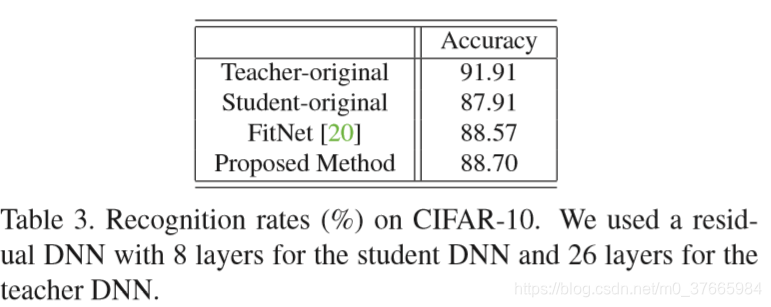
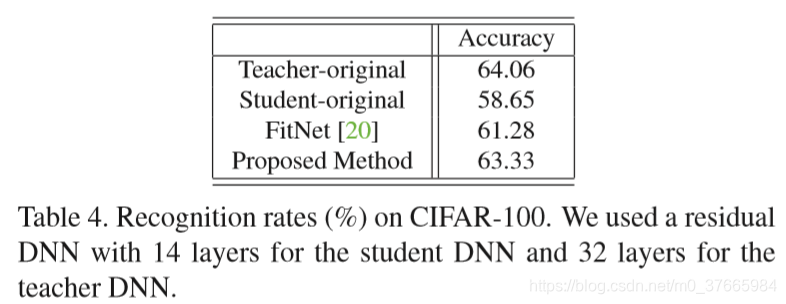
本次实验student网络的深度要小于teacher网络的深度

  迁移学习

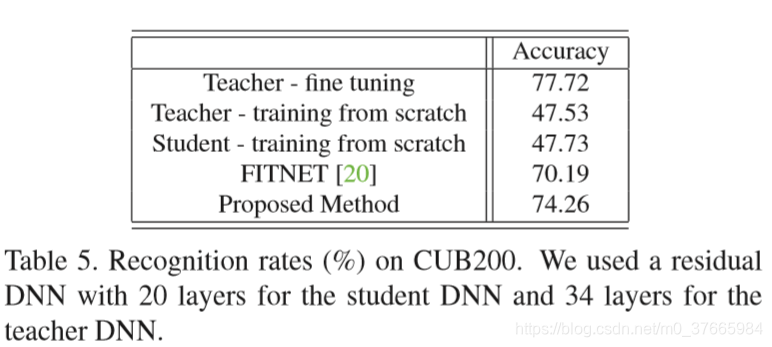
Teacher-fine tuning是在34层的网络上进行迁移学习得到的结果，Proposed Method是在20层的网络上进行FSP学习得到的结果，可以看出，已经很接近了。

结论

提出了以解决问题的流的方式来进行知识蒸馏

从三个方面验证了提出的方法的有效性

这篇关于A Gift from Knowledge Distillation: Fast Optimization,Network Minimization and Transfer Learning论文初读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/705800。

相关文章

poj 2349 Arctic Network uva 10369（prim or kruscal最小生成树）

poj 2349 Arctic Network uva 10369（prim or kruscal最小生成树）

题目很麻烦，因为不熟悉最小生成树的算法调试了好久。 感觉网上的题目解释都没说得很清楚，不适合新手。自己写一个。 题意：给你点的坐标，然后两点间可以有两种方式来通信：第一种是卫星通信，第二种是无线电通信。 卫星通信：任何两个有卫星频道的点间都可以直接建立连接，与点间的距离无关； 无线电通信：两个点之间的距离不能超过D，无线电收发器的功率越大，D越大，越昂贵。 计算无线电收发器D
阅读更多...
AI hospital 论文Idea

AI hospital 论文Idea

一、Benchmarking Large Language Models on Communicative Medical Coaching: A Dataset and a Novel System论文地址含代码 大多数现有模型和工具主要迎合以患者为中心的服务。这项工作深入探讨了LLMs在提高医疗专业人员的沟通能力。目标是构建一个模拟实践环境，人类医生（即医学学习者）可以在其中与患者代理进行医学
阅读更多...
论文翻译：arxiv-2024 Benchmark Data Contamination of Large Language Models: A Survey

论文翻译：arxiv-2024 Benchmark Data Contamination of Large Language Models: A Survey

Benchmark Data Contamination of Large Language Models: A Survey https://arxiv.org/abs/2406.04244 大规模语言模型的基准数据污染：一项综述 文章目录 大规模语言模型的基准数据污染：一项综述摘要1 引言 摘要 大规模语言模型（LLMs），如GPT-4、Claude-3和Gemini的快
阅读更多...
论文阅读笔记: Segment Anything

论文阅读笔记: Segment Anything

文章目录 Segment Anything摘要引言任务模型数据引擎数据集负责任的人工智能 Segment Anything Model图像编码器提示编码器mask解码器解决歧义损失和训练 Segment Anything 论文地址: https://arxiv.org/abs/2304.02643 代码地址:https://github.com/facebookresear
阅读更多...
论文翻译：ICLR-2024 PROVING TEST SET CONTAMINATION IN BLACK BOX LANGUAGE MODELS

论文翻译：ICLR-2024 PROVING TEST SET CONTAMINATION IN BLACK BOX LANGUAGE MODELS

PROVING TEST SET CONTAMINATION IN BLACK BOX LANGUAGE MODELS https://openreview.net/forum?id=KS8mIvetg2 验证测试集污染在黑盒语言模型中 文章目录 验证测试集污染在黑盒语言模型中摘要1 引言 摘要 大型语言模型是在大量互联网数据上训练的，这引发了人们的担忧和猜测，即它们可能已
阅读更多...
OmniGlue论文详解（特征匹配）

OmniGlue论文详解（特征匹配）

OmniGlue论文详解（特征匹配） 摘要1. 引言2. 相关工作2.1. 广义局部特征匹配2.2. 稀疏可学习匹配2.3. 半稠密可学习匹配2.4. 与其他图像表示匹配 3. OmniGlue3.1. 模型概述3.2. OmniGlue 细节3.2.1. 特征提取3.2.2. 利用DINOv2构建图形。3.2.3. 信息传播与新的指导3.2.4. 匹配层和损失函数3.2.5. 与Super
阅读更多...
BERT 论文逐段精读【论文精读】

BERT 论文逐段精读【论文精读】

BERT: 近 3 年 NLP 最火 CV: 大数据集上的训练好的 NN 模型，提升 CV 任务的性能 —— ImageNet 的 CNN 模型 NLP: BERT 简化了 NLP 任务的训练，提升了 NLP 任务的性能 BERT 如何站在巨人的肩膀上的？使用了哪些 NLP 已有的技术和思想？哪些是 BERT 的创新？ 1标题 + 作者 BERT: Pre-trainin
阅读更多...
[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

引言 今天带来第一篇量化论文LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale笔记。 为了简单，下文中以翻译的口吻记录，比如替换"作者"为"我们"。 大语言模型已被广泛采用，但推理时需要大量的GPU内存。我们开发了一种Int8矩阵乘法的过程，用于Transformer中的前馈和注意力投影层，这可以将推理所需
阅读更多...
简单的Q-learning|小明的一维世界(3)

简单的Q-learning|小明的一维世界(3)

简单的Q-learning|小明的一维世界(1) 简单的Q-learning|小明的一维世界(2) 一维的加速度世界 这个世界，小明只能控制自己的加速度，并且只能对加速度进行如下三种操作：增加1、减少1、或者不变。所以行动空间为： { u 1 = − 1 , u 2 = 0 , u 3 = 1 } \{u_1=-1, u_2=0, u_3=1\} {u1​=−1,u2​=0,u3​=1}
阅读更多...
简单的Q-learning|小明的一维世界(2)

简单的Q-learning|小明的一维世界(2)

上篇介绍了小明的一维世界模型 、Q-learning的状态空间、行动空间、奖励函数、Q-table、Q table更新公式、以及从Q值导出策略的公式等。最后给出最简单的一维位置世界的Q-learning例子，从给出其状态空间、行动空间、以及稠密与稀疏两种奖励函数的设置方式。下面将继续深入，GO！ 一维的速度世界 这个世界，小明只能控制自己的速度，并且只能对速度进行如下三种操作：增加1、减
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2