传送门：【ZOJ】2539 Energy Minimization 题目分析：还是项目分配问题，还是曾经的味道TＵT 再次请出神奇的函数： 再看看题目中的函数： 惊人的相似啊有木有！简直就是稍作修改就好了。。 因为Xi只能取0或1，所以最终我们可以将所有的Xi分成两个集合：Xi取1的集合，Xi取0的集合。 假设源点S和Xi取1的集合相连，汇点T和Xi取0的集合相

You are given two arrays aa and bb, both of length nn. You can perform the following operation any number of times (possibly zero): select an index ii (1≤i≤n1≤i≤n) and swap aiai and bibi. Let's defi

一、前言 最近因为对结构化多任务学习，以及对带范数目标函数求解的学习，一直都很想求解带L2,1范数的目标函数（其实这只是个过程），针对这样的不光滑目标函数，梯度下降法并不合适。 虽然sklearn中的MultiTaskLasso也是这样的目标函数，并且使用了坐标下降法来求解，但是当目标函数中的损失函数也用L2,1范数时我又懵圈了。 正当我琢磨是不是能把两部分合在一起求解一个L2,1范数时（其

加权核范数（WNNM）最小化及其在图像去噪中的应用——学习笔记 前景提要不同权重 w w w条件下的求解方法权重按非升序排列 w 1 ≥ ⋅ ⋅ ≥ w n ≥ 0 w_1≥··≥w_n≥0 w1​≥⋅⋅≥wn​≥0权重按任意序排列权重按非降序排列 0 ≤ w 1 ≤ ⋅ ⋅ ≤ w n 0≤w_1≤··≤w_n 0≤w1​≤⋅⋅≤wn​ WNNM在图像去噪中的应用 前景提要

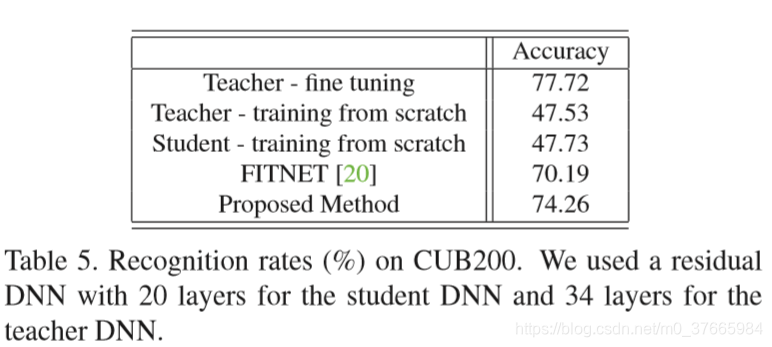
目录 摘要 引言 相关工作   知识迁移   快速优化   迁移学习 方法   提出观点   数学表达式   FSP Matrix的损失   学习步骤 实验   快速优化   性能的提升   迁移学习 结论 摘要 提出了将蒸馏的知识看作成一种解决问题的流，它是在不同层之间的feature通过内积计算得到的 这个方法有三个好处：   student网络可以