本文主要是介绍Tensorflow基础(四)--激活函数(Sigmoid、tanh);损失函数(二次代价函数、交叉熵代价函数、对数释然代价函数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 1.激活函数
- 1.1双曲正切函数与Sigmoid函数
- 2.损失函数(代价函数)
- 2.1 L1范数损失函数
- 2.2 L2范数损失函数
- 2.3 二次代价函数
- 2.4 交叉熵代价函数
- 2.5 对数释然代价函数(log-likelihood cost)
- 3.演示代码
1.激活函数
激活函数的想法来自对人脑中神经元工作机理的分析。神经元在某个阈值(也称活化电位)之上会被激活。大多数情况下,激活函数还意在将输出限制在一个小的范围内。
1.1双曲正切函数与Sigmoid函数
如下图展示了tanh与Sigmoid激活函数:
演示代码如下:

2.损失函数(代价函数)
损失函数(代价函数)是用来最小化以得到模型每个参数的最优值的。比如说,为了用预测器(X)来预测目标(y)的值,需要获得权重值(斜率)和偏置量(y截距)。得到斜率和y截距最优值的方法就是最小化代价函数/损失函数/平方和。对于任何一个模型来说,都有很多参数,而且预测或进行分类的模型结构也是通过参数的值来表示的。
你需要计算模型,并且为了达到这个目的,你需要定义代价函数(损失函数)。最小化损失函数就是为了寻找每个参数的最优值。对于回归/数值预测问题来说,L1或L2是很有用的损失函数。对于分类问题来说,交叉熵是很有用的损失函数。Softmax或者Sigmoid交叉熵都是非常流行的损失函数
2.1 L1范数损失函数
L1范数损失函数,也被称为最小绝对值偏差(LAD),最小绝对值误差(LAE)。总的说来,它是把目标值(Yi)与估计值(f(xi))的绝对差值的总和(S)最小化:
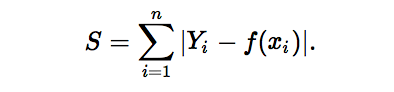
2.2 L2范数损失函数
L2范数损失函数,也被称为最小平方误差(LSE)。总的来说,它是把目标值(Yi)与估计值(f(xi))的差值的平方和(S)最小化:
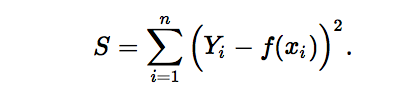
2.3 二次代价函数

C表示代价函数,x表示样本,y表示实际值,a表示输出值,n表示样本的总数。
为简单起见 ,以假如只有一个样本为例进行说明,
a=σ(z), z=∑Wj*Xj+b
σ() 是激活函数
此时二次代价函数为:


从上面可以看出二次代价函数W,b的梯度变化是与激活函数有关的。

- 假设我们的收敛目标是1。A点为0.82,距离目标较远,而A点梯度较大,权值调整较大,B点为0.98,距离目标较近,而B点梯度较小,权值调整较小。因此,它能够很快的从A点调整到B点,再慢慢向1收敛,这个方案是合理的。
- 假设我们的收敛目标是0。B点为0.98,距离目标较远,而B点梯度较小,权值调整较小,A点为0.82,距离目标较近,而A点梯度较大,权值调整较大。因此,它如果从B点开始,它会在B点经历很长一段时间才能到A,那么这个方案是不合理的。
如果误差比较大,说明离我们的目标比较远,此时权值调整的应该比较大,这是我们觉得比较合理的情况。
2.4 交叉熵代价函数


2.5 对数释然代价函数(log-likelihood cost)
对数释然函数常用来作为softmax回归的代价函数,如果输出层神经元是sigmoid函数,可以采用交叉熵代价函数。而深度学习中更普遍的做法是将softmax作为最后一层,此时常用的代价函数是 对数释然代价函数。
对数似然代价函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数释然代价函数 在二分类时可以化简为交叉熵代价函数的形式。
在Tensorflow中用:
tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉熵。 tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉熵。
3.演示代码
修改3-2简单实现手写数字识别代码,使用softmax交叉熵代价函数:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#载入数据集
mnist = input_data.read_data_sets("MNIST_data",one_hot=True)#每个批次的大小
batch_size = 50
#计算一共有多少个批次
n_batch = mnist.train.num_examples // batch_size#定义两个placeholder
x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])#创建一个简单的神经网络
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x,W) + b)#二次代价函数
# loss = tf.reduce_mean(tf.square(y-prediction))
#使用softmax交叉熵代价函数
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用梯度下降法进行训练
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)#初始化变量
init = tf.global_variables_initializer()#结果存放在一个布尔型列表中
#argmax返回一维张量中最大值所在的位置
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))
#求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))with tf.Session() as sess:sess.run(init)for epoch in range(21):for batch in range(n_batch):batch_xs,batch_ys = mnist.train.next_batch(batch_size)sess.run(train_step,feed_dict = {x:batch_xs,y:batch_ys})acc = sess.run(accuracy,feed_dict = {x:mnist.test.images,y:mnist.test.labels})print("Iter"+str(epoch)+",Testing Accuracy"+str(acc))
运行结果对比
#二次代价函数的结果
Iter0,Testing Accuracy0.8703
Iter1,Testing Accuracy0.8876
Iter2,Testing Accuracy0.8964
Iter3,Testing Accuracy0.9018
Iter4,Testing Accuracy0.9047
Iter5,Testing Accuracy0.9069
Iter6,Testing Accuracy0.9094
Iter7,Testing Accuracy0.9108
Iter8,Testing Accuracy0.9121
Iter9,Testing Accuracy0.9135
Iter10,Testing Accuracy0.9145
Iter11,Testing Accuracy0.9155
Iter12,Testing Accuracy0.9166
Iter13,Testing Accuracy0.9176
Iter14,Testing Accuracy0.9176
Iter15,Testing Accuracy0.9183
Iter16,Testing Accuracy0.9186
Iter17,Testing Accuracy0.9192
Iter18,Testing Accuracy0.9195
Iter19,Testing Accuracy0.919
Iter20,Testing Accuracy0.9205
#交叉熵代价函数结果
Iter0,Testing Accuracy0.8944
Iter1,Testing Accuracy0.9054
Iter2,Testing Accuracy0.9099
Iter3,Testing Accuracy0.9134
Iter4,Testing Accuracy0.9148
Iter5,Testing Accuracy0.9167
Iter6,Testing Accuracy0.9202
Iter7,Testing Accuracy0.9207
Iter8,Testing Accuracy0.9211
Iter9,Testing Accuracy0.9214
Iter10,Testing Accuracy0.9214
Iter11,Testing Accuracy0.9222
Iter12,Testing Accuracy0.9228
Iter13,Testing Accuracy0.9237
Iter14,Testing Accuracy0.924
Iter15,Testing Accuracy0.9245
Iter16,Testing Accuracy0.9238
Iter17,Testing Accuracy0.9245
Iter18,Testing Accuracy0.9244
Iter19,Testing Accuracy0.9251
Iter20,Testing Accuracy0.9251
从结果可以看出,当准确率达到0.909时,使用二次代价函数需要迭代6次,而使用softmax交叉熵函数只迭代了2次,这很明显地看出使用交叉熵代价函数速度会快很多。
结论
所以我们在使用S型激活函数或者softmax的时候,就应该采用交叉熵代价函数,这样效率会比较高。
这篇关于Tensorflow基础(四)--激活函数(Sigmoid、tanh);损失函数(二次代价函数、交叉熵代价函数、对数释然代价函数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







