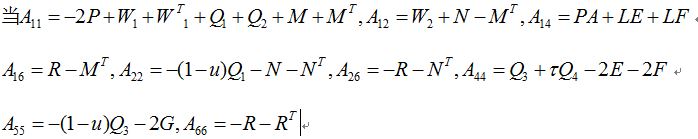本文主要是介绍LMI工具箱求解线性矩阵不等式(2),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上次的文章介绍了最基本的线性矩阵不等式的求法,今天我们来介绍比较复杂的线性矩阵不等式的求法。
C=[1 0;0 1];A=[1.5 3;1 2];B=[3 0.1;0.2 2.5];b=1.5,u=0.5, L=I,以下均为二阶矩阵,存在对称正定矩阵P,Q_i (i =1,2,3,4),三个正定对角矩阵E,F,G,矩阵M,N,R,W_1,W_2,使得如下LMI成立。
上一次已经介绍过A11的构造方法,接下来我们来介绍其他几个的构造方法:
A12=W2+N-M',为第一行第二列,所以termID=[1 1 2 x],因为W2为普通矩阵,所以可以写为W2=lmivar(2,[2 2]),N,M同理。
定义完之后,就可以表述A12的内容。因为W2左乘1,右乘1,所以总的可以写为lmiterm([1 1 2 W2],1,1);同理N的表述为lmiterm([1 1 2 N],1,1);在这里构造的时候,M的转置为在termID表述为-M,左乘-1,右乘1,所以表述为lmiterm([1 1 2 -M],-1,1)。
A14=PA+LE+LF,为第一行第四列,所以termID=[1 1 4 x],P前面已经定义过,不需要再定义,A,L为已知矩阵,E,F为正定对角矩阵,所以可以定义为E=lmivar(1,[1 0;1 0]),同理F。
定义完之后,就可以表述A14的内容。因为P左乘1,右乘A,所以可写为lmiterm([1 1 4 P],1,A);E左乘L,右乘1,所以表述为lmiterm([1 1 4 E],L,1);同理F为lmiterm([1 1 4 F],L,1)。
其他的基本同理,就不再赘述,附结果如下:
lmiterm([1 1 5 p],1,b);
lmiterm([1 1 6 r],1,1);lmiterm([1 1 6 -m],-1,1);
lmiterm([1 2 2 q1],-0.5,1);lmiterm([1 2 2 n],-1,1);lmiterm([1 2 2-n],-1,1);
lmiterm([1 2 6 r],-1,1);lmiterm([1 2 6 -n],-1,1);
lmiterm([1 3 3 q2],-1,1);
lmiterm([1 4 4 q3],1,1);lmiterm([1 4 4 q4],1.5,1);lmiterm([1 4 4 e],-2,1);
lmiterm([1 4 4 f],-2,1);
lmiterm([1 5 5 q3],-0.5,1);lmiterm([1 5 5 g],-2,1);
lmiterm([1 6 6 r],-1,1);lmiterm([1 6 6 -r],-1,1);
lmiterm([-2,1 1 p],1,1);
lmiterm([-3,1 1 q1],1,1);
lmiterm([-4,1 1 q2],1,1);
lmiterm([-5,1 1 q3],1,1);
lmiterm([-6,1 1 q4],1,1);
lmiterm([-7,1 1 e],1,1);
lmiterm([-8,1 1 f],1,1);
lmiterm([-9,1 1 g],1,1);
再用:
lmisys=getlmis;
[tmin,xfeas]=feasp(lmisys)
根据得出的tmin判断是否有解。
这篇关于LMI工具箱求解线性矩阵不等式(2)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!