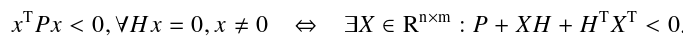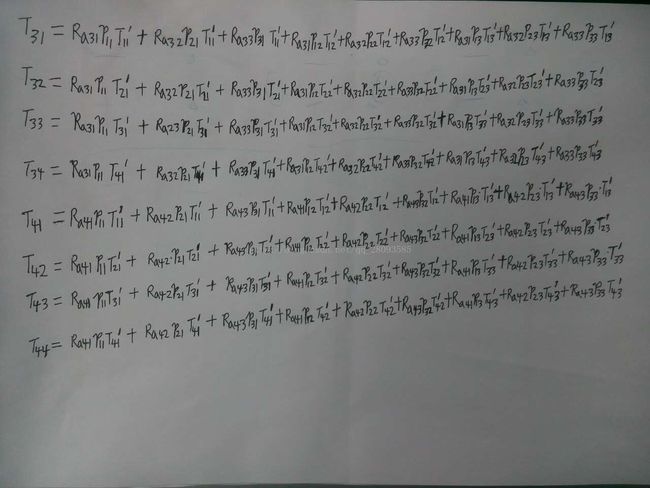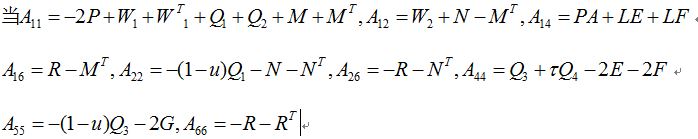lmi专题
LMI Gocator GoSDK C#开发学习笔记(二)
命名空间Lmi3d.Zen KVersion结构 定义:public struct KVersion 描述:表示版本号。 公共成员字段Major 定义:public int Major { get; } 描述:返回版本号的主要部分。 公共成员字段Minor 定义:public int Minor { get; } 描述:返回版本号的次要部分。 公共成员字段Release 定义
LMI(线性矩阵不等式)、schur补 学习笔记
1.掌握求解LMI的目的(以及整套流程) 掌握matlab中LMI工具箱的函数使用 2.掌握schurs补 -------------------------------------------------- 你的点赞是我更新的动力! -------------------------------------------------- 一.掌握求解LMI的目的(以及整套流程)
线性矩阵不等式(LMI)在控制理论中的应用
目录 (一)Matlab中的LMI处理工具包 (二)为什么LMI成为控制理论领域重要工具? (三)LMI在与Lyapunov不等式的关系 (1)线性矩阵不等式 (2)线性矩阵不等式系统 (3)舒尔(Schur)补 (四)LMI中常见引理 引理2(广义KYP引理[4]) 推论1(广义KYP引理推论[4]) 引理3(射影定理[1]) 引理4 (Jensen不等式[5,6]
基于LMI的非线性混沌系统滑模控制
目录 前言 1.非线性系统 2.控制器设计 3.仿真分析 3.1仿真混沌系统 3.2 LMI求解反馈阵F 3.3仿真模型 3.4仿真结果 3.5注意事项 前言 前面我们介绍了很多种滑模面设计,以及介绍了几篇结合LMI的滑模控制,其核心思想可以看作是用LMI去控制非线性的状态反馈部分,滑模去做线性的鲁棒部分,本篇博客介绍一篇非线性系统的滑模控制。 1.非
基于LMI的非线性混沌系统滑模控制
目录 前言 1.非线性系统 2.控制器设计 3.仿真分析 3.1仿真混沌系统 3.2 LMI求解反馈阵F 3.3仿真模型 3.4仿真结果 3.5注意事项 前言 前面我们介绍了很多种滑模面设计,以及介绍了几篇结合LMI的滑模控制,其核心思想可以看作是用LMI去控制非线性的状态反馈部分,滑模去做线性的鲁棒部分,本篇博客介绍一篇非线性系统的滑模控制。 1.非
matlab lmi两个未知数,Matlab复杂LMI仿真实例
(1)仿真的论文题目: A PD-Like Protocol With a Time Delay to Average Consensus Control for Multi-Agent Systems Under an Arbitrarily Fast Switching Topology Dong Wang, Ning Zhang, Jianliang Wang, Senior Member
matlab lmi两个未知数,Matlab复杂LMI仿真实例
(1)仿真的论文题目: A PD-Like Protocol With a Time Delay to Average Consensus Control for Multi-Agent Systems Under an Arbitrarily Fast Switching Topology Dong Wang, Ning Zhang, Jianliang Wang, Senior Member
LMI工具箱求解线性矩阵不等式(2)
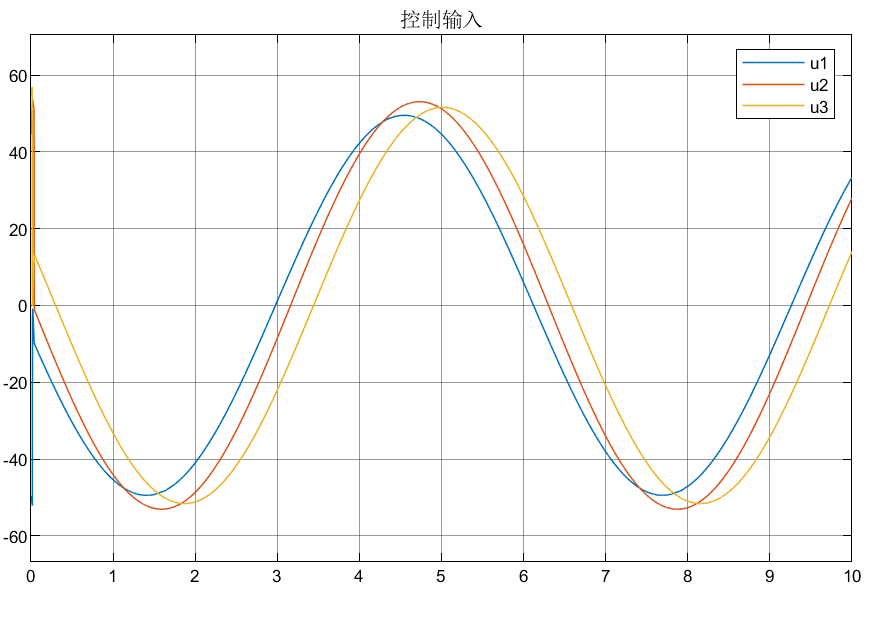
上次的文章介绍了最基本的线性矩阵不等式的求法,今天我们来介绍比较复杂的线性矩阵不等式的求法。 C=[1 0;0 1];A=[1.5 3;1 2];B=[3 0.1;0.2 2.5];b=1.5,u=0.5, L=I,以下均为二阶矩阵,存在对称正定矩阵P,Q_i (i =1,2,3,4),三个正定对角矩阵E,F,G,矩阵M,N,R,W_1,W_2,使得如下LMI成立。 上一次已经介绍过A
LMI工具箱求解线性矩阵不等式(2)
上次的文章介绍了最基本的线性矩阵不等式的求法,今天我们来介绍比较复杂的线性矩阵不等式的求法。 C=[1 0;0 1];A=[1.5 3;1 2];B=[3 0.1;0.2 2.5];b=1.5,u=0.5, L=I,以下均为二阶矩阵,存在对称正定矩阵P,Q_i (i =1,2,3,4),三个正定对角矩阵E,F,G,矩阵M,N,R,W_1,W_2,使得如下LMI成立。 上一次已经介绍过A
基于LMI的等效滑模控制
目录 前言 1.一阶欠驱动倒立摆系统 2.基于LMI的等效滑模控制器 3.simulink仿真 3.1 simulink模型 3.2 结果分析 3.2 结论 前言 关于LMI和滑模控制的结合上两篇文章已有介绍和仿真分析,本篇文章再介绍一篇特别常见常用的基于LMI的等效滑模控制,并且结合一阶倒立摆模型进行仿真分析,并且考虑了模型的不确定性,继续看下去吧。 往期文章
基于LMI的等效滑模控制
目录 前言 1.一阶欠驱动倒立摆系统 2.基于LMI的等效滑模控制器 3.simulink仿真 3.1 simulink模型 3.2 结果分析 3.2 结论 前言 关于LMI和滑模控制的结合上两篇文章已有介绍和仿真分析,本篇文章再介绍一篇特别常见常用的基于LMI的等效滑模控制,并且结合一阶倒立摆模型进行仿真分析,并且考虑了模型的不确定性,继续看下去吧。 往期文章
Matlab中LMI(线性矩阵不等式)工具箱使用例子
我搜出来的都是一些简单的算例,并且机会没有中文教程,我在这里就斗胆把自己的体会写出来,试着给大家提供一点参考。 LMI:Linear Matrix Inequality,就是线性矩阵不等式。 在Matlab当中,我们可以采用图形界面的lmiedit命令,来调用GUI接口,但是我认为采用程序的方式更方便(也因为我不懂这个lmiedit的GUI)。 对于LMI Lab, 其中有三种求解器(solv
【转载】Matlab中LMI(线性矩阵不等式)工具箱使用教程
@TOC 转载 原文地址:https://www.cnblogs.com/Hand-Head/articles/5412511.html 这一段被老板逼着论文开题,自己找方向比较着急,最后选择了供应链控制理论的一个方向。我要写的论文,用到了Matlab的LMI工具,以及某篇论文中的H-inf稳定定理。自己好好研究了好长时间,怎么也无法实现该论文当中的算例。研究了一个多月,自己简直就快崩溃了,也搞
使用YALMIP工具箱来求解LMI
使用YALMIP工具箱来求解LMI 使用的例子为《滑模变结构控制MATLAB仿真基本理论与设计方法 第四版》第434页 工具:MATLAB 2016B YALMIP工具包 例子: 代码: A = [-2.548 9.1 0;1 -1 1;0 -14.2 0];B =[1 0 0;0 1 0;0 0 1];F = sdpvar(3,3);M = sdpvar(3,3);P = 1000
LMI FocalSpec 3D线共焦传感器 使用笔记1
一.硬件介绍 以上特别注意: 屏蔽线必须接地,因为在现场实际调试中,使用软件调试发现经常 弹窗 传感器丢失警告!! 以上 Position LED 的灯被钣金挡住,无法查看异常现象,能否将指示灯设置在软件界面上? 需要确认是软触发还是硬触发,理论上 硬触发比软触发速度要快.(我们目前使用的1620是高速传感器). 注意:弯折半径,光纤线在设备里最好