基于LMI的非线性混沌系统滑模控制

目录

前言

1.非线性系统

2.控制器设计

3.仿真分析

3.1仿真混沌系统

3.2 LMI求解反馈阵F 

3.3仿真模型

​​​​3.4仿真结果

3.5注意事项

前言

前面我们介绍了很多种滑模面设计，以及介绍了几篇结合LMI的滑模控制，其核心思想可以看作是用LMI去控制非线性的状态反馈部分，滑模去做线性的鲁棒部分，本篇博客介绍一篇非线性系统的滑模控制。

1.非线性系统

其控制目标为使状态变量x趋近于目标量xr，其中非线性函数f满足Lipschitz条件，即：，L为Lipschitz条件的矩阵。

2.控制器设计

定义误差变量z=x-xr，则误差变量导数z'=x'-xr'，这里可以将误差z看作为动态的滑模面，所以将z设计为滑模函数，设计如下形式的控制律：

其中：

①F为求解LMI得到的状态反馈增益，F=inv(PB)M；

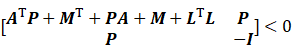
②ur=-Fxr-inv(B)(Axr+f(xr)-xr')为前馈控制项；

③us=-inv(B)(εsign(z))为滑模鲁棒项。

所以控制律变为：

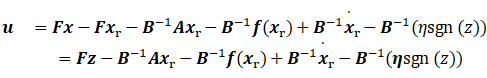
3.仿真分析

3.1仿真混沌系统

​​​​​​​

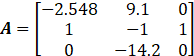
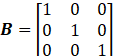
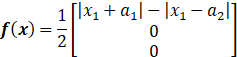
 Lipschitz矩阵L的选取：

当状态变量x∈[a,b]，f(x)为定义在该区间的连续光滑函数，根据中值定理有：f(a)-f(b)<f'(x)(a-b)，所以上述非线性函数f有如下不等式成立：

显然f'(x)是一个3x3的雅可比矩阵，且最大的元素即对x1的偏导为1，可以令L≥max(f'(x))，所以定义矩阵L为： 

3.2 LMI求解反馈阵F 

这里使用YALMIP工具箱求解，也可以使用maltab自带的LMI工具箱求解，具体求解就不再叙述了，往期文章有很多。

求解结果为：F =

   -1.5127   -5.0500    0.0001
   -5.0497   -2.6069    6.5995
    0.0001    6.6000   -3.6072

3.3仿真模型

这里选择初始的状态为[1 -1 -1]

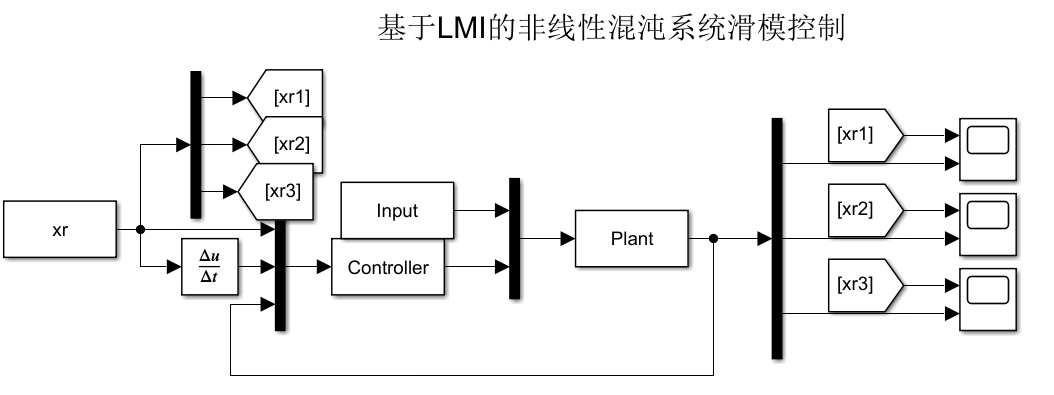
​​​​3.4仿真结果

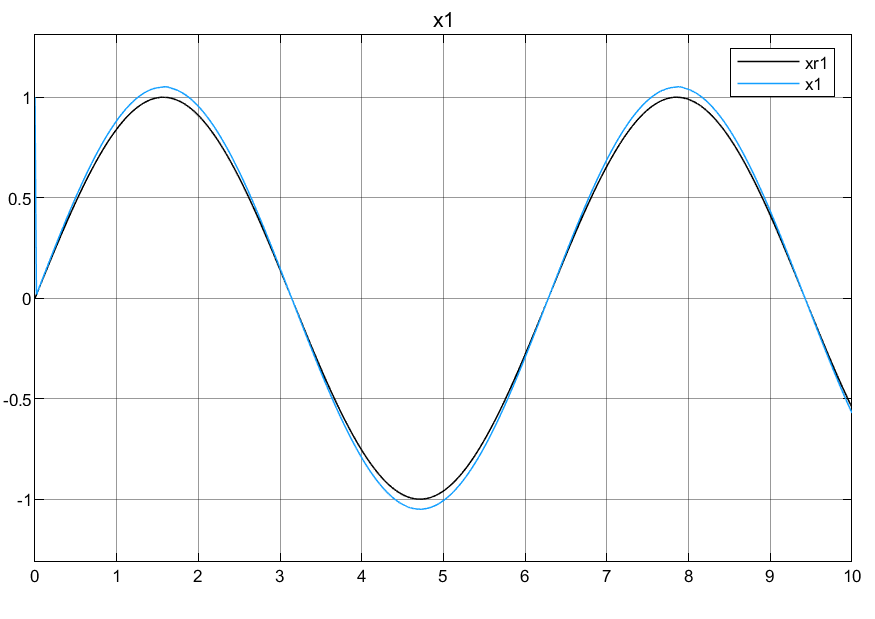
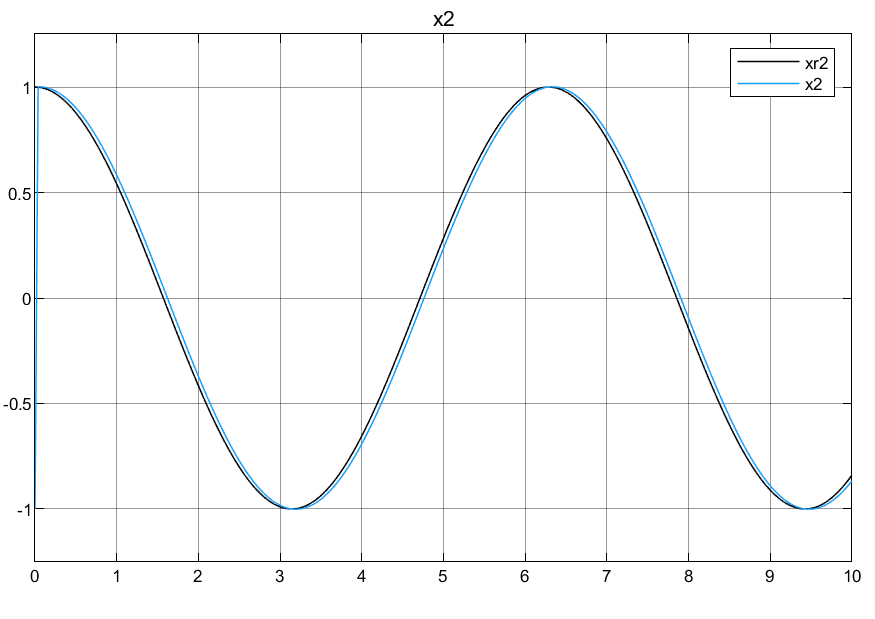
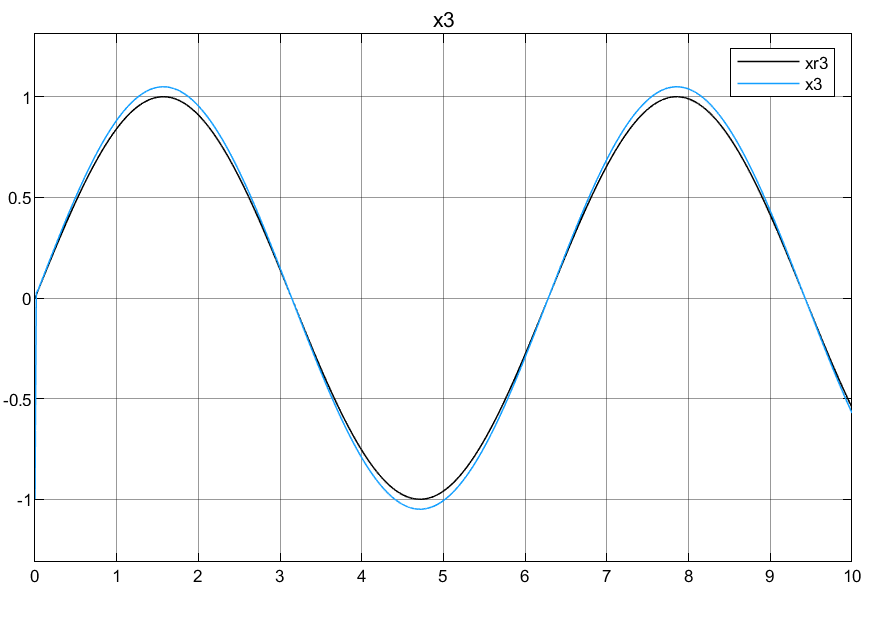
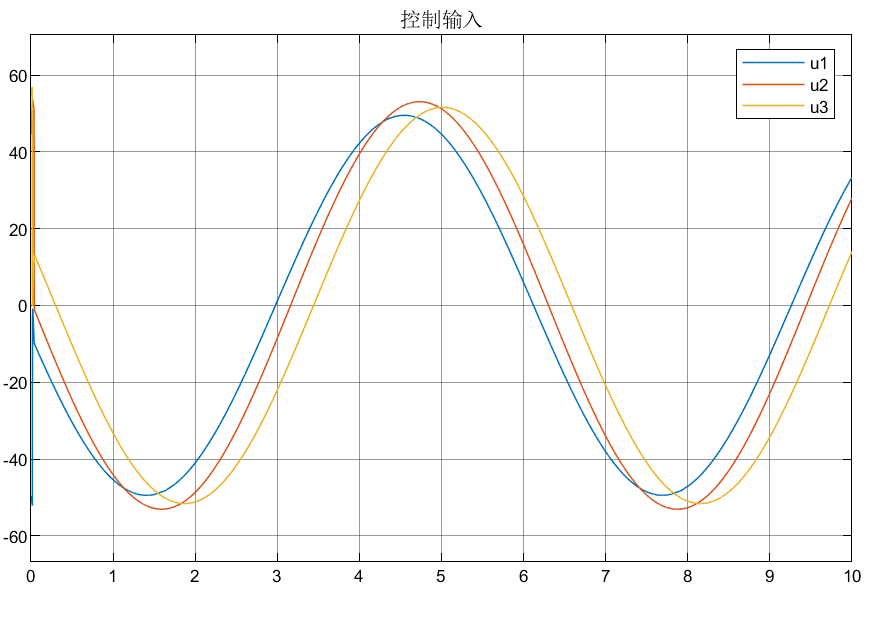
 总结：可以看到对于跟踪的效果在峰值的时候误差还是比较大的，效果不是特别理想，具体的原因等待后面的探索

3.5注意事项

①对于求解器的选择和步长的选择对仿真结果的影响还是比较大的，刚开始选择任意求解和任意步长的时候求解的效果较差，此外选择定步长为0.01时效果也很差，后面将步长调整到0.001才有了上面较好的效果。但是对于初始步长到跟踪目标所需的时间极短！

②对于L的选择冒失在这里影响不是很大，因为我试图将L增大重新求解F矩阵，但是仿真结果几乎相差不大，可能是LMI反馈项影响权重不是很大的原因。

如果有帮助，麻烦帮忙点个赞是我最大的分享动力，非常感谢！

注：仅为便利自己学习，错误在所难免，如有侵权，请联系删除，有兴趣的学者可以参考学习交流，谢谢！