matlab lmi两个未知数,Matlab复杂LMI仿真实例

(1)仿真的论文题目：

A PD-Like Protocol With a Time Delay to Average Consensus Control for Multi-Agent Systems Under an Arbitrarily Fast Switching Topology

Dong Wang, Ning Zhang, Jianliang Wang, Senior Member, IEEE, and Wei Wang

(2)仿真内容：其中提出的Theorem 1，固定时滞下的一种Lyapunov方程

(3)这个式子中的第一个 LMI 比较复杂，一般的 LMI 描述方式难以描述。

分析：矩阵P的大小是3n*3n，将R,W,Q,Y,S都是n*n的，ra 和T矩阵都是4n*3n的。

1.将P矩阵转化为3*3分块矩阵，ra和T分割为4*3的分块矩阵。 块矩阵都是n*n的:

%把P定义为9个n*n的子块矩阵

[P11,~,SP11]=lmivar(1,[10 1]);

[P22,~,SP22]=lmivar(1,[10 1]);

[P33,~,SP33]=lmivar(1,[10 1]);

[P12,~,SP12]=lmivar(2,[10 10]);

[P13,~,SP13]=lmivar(2,[10 10]);

[P23,~,SP23]=lmivar(2,[10 10]);

[P21,~,SP21]=lmivar(3,SP12');

[P31,~,SP31]=lmivar(3,SP13');

[P32,~,SP32]=lmivar(3,SP23');

%P是3n*3n的

[P,~,SP]=lmivar(3,[SP11,SP12,SP13;SP21,SP22,SP23;SP31,SP32,SP33]);

RA=cell(4,3);

T =cell(4,3);

%把RA和T分成分块矩阵

for i=1:4

for j=1:3

RA{i,j}=ra(10*i-9:10*i,10*j-9:10*j);%[1 2 4;1 1 1;2 3 4;]

T{i,j}=t(10*i-9:10*i,10*j-9:10*j);

end

end

2.将P,RA,T的分块矩阵带入第一个矩阵不等式乘开：(下面是ra*P*T'的乘开的结果)

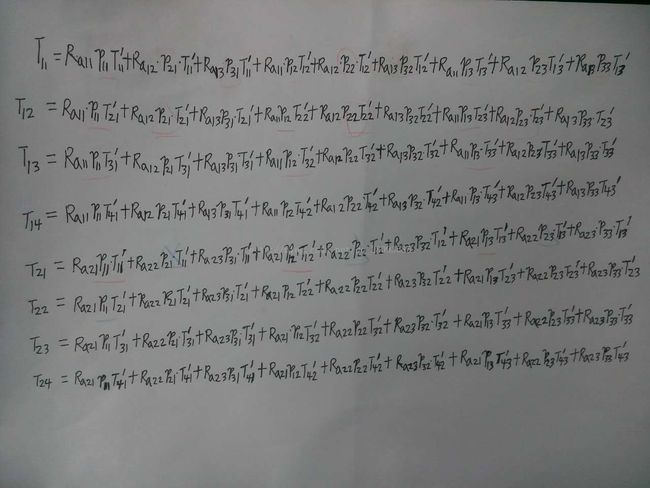
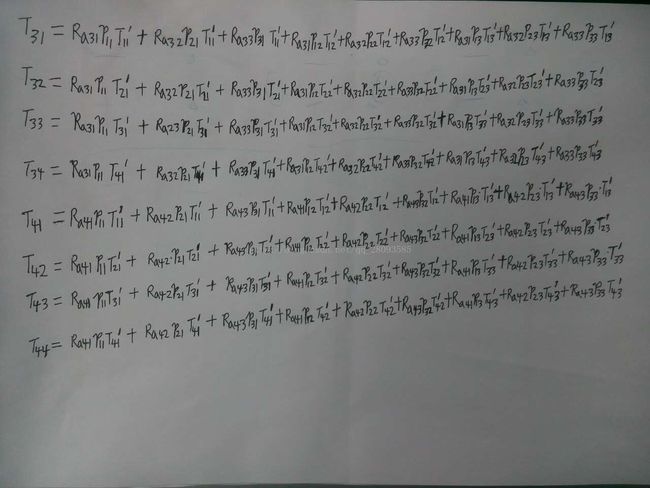
3.同理乘开T*P*ra'

4.之后就可以用一般的LMI方法输入第一个LMI的转化结果和其他的LMI，然后求解。