优化｜求解非凸和无梯度lipschitz连续性的一阶算法在二次规划反问题中的应用(代码分享)

本文主要是介绍优化｜求解非凸和无梯度lipschitz连续性的一阶算法在二次规划反问题中的应用(代码分享)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文信息（包括题目、发表期刊、原文链接等）：First Order Methods Beyond Convexity and Lipschitz Gradient Continuity with Applications to Quadratic Inverse Problems
原文作者：Jérôme Bolte, Shoham Sabach, Marc Teboulle, and Yakov Vaisbourd
代码分享者：李朋

1 问题描述

考虑下面的二次规划反问题
$$\min \{\Psi (x):=g(x)+\theta f(x):x\in {\mathbb{R}}^d\}$$

其中 $g(x)=\frac{1}{4}{\sum }_{i=1}^m(x^T{A}_{i}x-b_i{)}^2,f(x)=\Vert x{\Vert }_1$，而且 $A_i$是对称矩阵。

2 求解方法

在给出求解方法之前，我们首先定义
$$p_{\lambda }(x)=\lambda \nabla g(x)-\nabla h(x)$$
和软阈值算子
S τ ( y ) = max ⁡ { ∣ y ∣ − τ , 0 } sgn ( y ) = max ⁡ ( y − τ , 0 ) − max ⁡ ( − y − τ , 0 ) ( 5.1 ) S_{\tau}(y)=\max\{|y|-\tau, 0\}\text{sgn}(y)=\max(y-\tau,0) - \max(-y-\tau,0) \qquad (5.1) Sτ​(y)=max{∣y∣−τ,0}sgn(y)=max(y−τ,0)−max(−y−τ,0)(5.1)
为保证函数$g(x),f(x)$是L-smad，我们令
$$h(x)=\frac{1}{4}\Vert x{\Vert }_2^4+\frac{1}{2}\Vert x{\Vert }_2^2,$$
具体见原文引理5.1。

本文的求解方法主要根据原文的命题5.1，如下所示

命题5.1 ($l_1$范数正则化的Bregman近似公式) 令$f=\Vert \cdot {\Vert }_1$且对$x\in {\mathbb{R}}^d$，令$v(x):=S_{\lambda \theta }(p_{\lambda }(x))$。那么，可得$x^{+}=T_{\lambda }(x)$为
$$x^{+}=-t^{\ast }v(x)=t^{\ast }{S}_{\lambda \theta }(\nabla h(x)-\lambda \nabla g(x))(5.2)$$

是显示公式，其中$t^{\ast }$是下面方程的唯一正实根，
$$t^3\Vert v(x){\Vert }_2^2+t-1=0.(5.3)$$

3 代码实现

在本次仿真中，我们采用Julia语言编写一个求解二次规划反问题的算法 (5-2)。

(1) 用using 添加一些要用到的库。

using Roots
using LinearAlgebra
using SparseArrays
using Distributions
using Random
using Printf
using Plots
using Polynomials

(2) 根据公式 (5-1) 定义软阈值函数

function compute_softThreshold(y,τ)p = max.(y.-τ,0) - max.(-y.-τ,0);return p;
end

(3)根据公式(5-3) 计算$t^{\ast }$

function find_positiveRoot(S)t = variable();v = sum(S.^2);f = t^3*v + t -1;t_opt = find_zero(f,(0,1));return t_opt;
end

(4) 计算$g(x)=\frac{1}{4}{\sum }_{i=1}^m(x^T{A}_{i}x-b_i{)}^2$的导数

function derivative_g(A,b,x,m,n)# compute the derivative of g(x)der = zeros(n,1);for k in range(1,m)der = der + (transpose(x)*A[k]*x.-b[k]).*(A[k]*x);endreturn der;
end

(5) 计算$h(x)=\frac{1}{4}\Vert x{\Vert }_2^4+\frac{1}{2}\Vert x{\Vert }_2^2$的导数

function derivative_h(x)# compute the derivative of h(x)der = (sum(x.^2) + 1).*x;return der;
end

(6) 全局参数

# Global Parameters
MAXITE = 500;
m =3;
n = 2;

(7) 生成问题数据

θ = 0.5;Random.seed!(123);A = Array{Matrix}(undef,m);
b = Array{Float64}(undef,m); d = Normal(2,2);
for k in range(1,m)A[k] = rand(d,n,n)A[k] = (transpose(A[k])+A[k])./2
endfor k in range(1,m)b[k] = rand(d,1)[1];
end

(8) 根据引理5.1的结果可知$L\ge {\sum }_{i=1}^{m}3\Vert A_i{\Vert }^2+\Vert A_i\Vert |b_i|$。另外，根据定理 4.1 成立的条件$0<\lambda L<1$，可得 $0<\lambda <\frac{1}{L}$。

L = sum([3*norm(A[k]).^2 + norm(A[k])*norm(b[k]) for k =1:m])+1;
λ = 1/L;   #λ≤1/L

(9) 主程序

x = ones(n,1)
objval_vec = zeros(1,MAXITE);  #存储计算过程中目标函数值
x_vec = zeros(n,MAXITE);       #存储计算过程中变量值for k in range(1,MAXITE)#计算、存储当前目标函数值objval = sum([1/4*(transpose(x)*A[k]*x.-b[k])^2 for k=1:m]) .+ θ.*norm(x,1); objval_vec[1,k] = objval[1,1];  #存储当前变量值x_vec[:,k] = x; #计算函数g(x)、h(x)当前时刻的导数值xold = x;der_h = derivative_h(xold);der_g = derivative_g(A,b,xold,m,n);y = λ*der_g - der_h;τ = λ * θ;v = compute_softThreshold(y,τ);   #计算公式(5-2)中的软阈值算子部分   topt = find_positiveRoot(v);  #计算公式(5-2)中的 t*x = -topt.*v; # 根据公式(5-2) 求出下一时刻 x 的值
end
print("最优解：",x,"\n");
print("最小目标值：",objval_vec[end]);

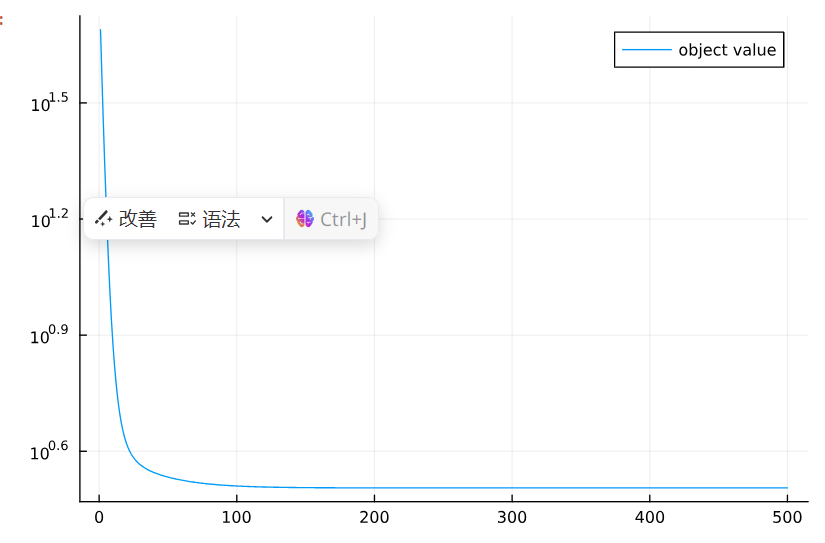
(10) 画出目标函数值随计算步数的变化

K = range(1, MAXITE);
plot(K, [objval_vec[k] for k=1:MAXITE], yaxis=:log10,label="object value")

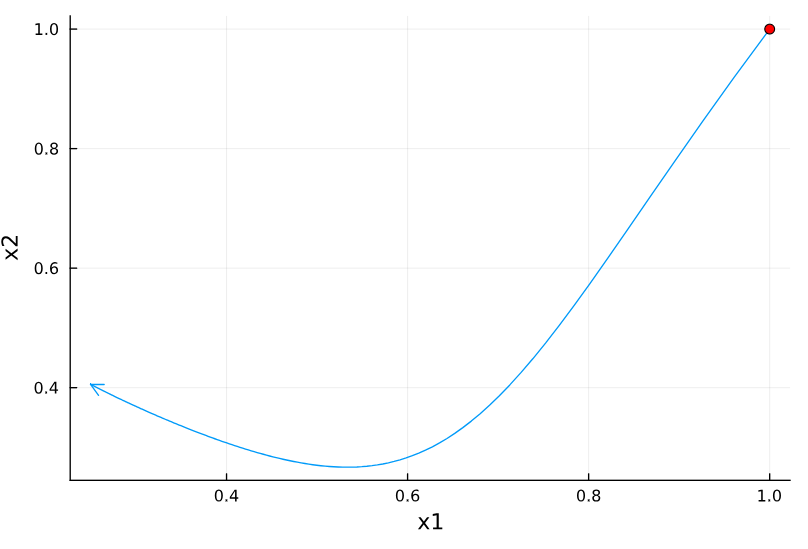
(11) 画出变量值随计算步数的变化

plot(x_vec[1,1:MAXITE], x_vec[2,1:MAXITE], arrow = :arrow)
scatter!([x_vec[1,1]], [x_vec[2,1]], markshape=:rect, marksize = 5, markercolor= :red, legend = false)
xlabel!("x1")
ylabel!("x2")

这篇关于优化｜求解非凸和无梯度lipschitz连续性的一阶算法在二次规划反问题中的应用(代码分享)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---