本文主要是介绍ctr 校准纠偏,保序回归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
此文尚未完成.
背景
模型预测的 ctr 并不一定总是准的, 若只关注 auc 指标, 难以反映业务价值.
场景一: 广告出价
排序表达式是 final_score = ctr * bid_price.
ABC三条广告, A的实际点击率是10%,B的实际点击率是5%,C的实际点击率是1%,但是A B C的点击收益分别是2,5,10。
如果我们的模型只保序、没有做到保距,那么输出的预估值是5%,1%,0.5%,这样的话AUC的排序指标是满足了,但是实际收益并不是最优的。
表格直观展现见下:
| before | A | B | C |
|---|---|---|---|
| ctr | 0.05 | 0.01 | 0.005 |
| bid_price | 2 | 5 | 10 |
| 预估收益 | 0.1 | 0.05 | 0.05 |
此时排序为: A,B,C
| after 纠偏 | A | B | C |
|---|---|---|---|
| ctr | 0.1 | 0.05 | 0.01 |
| bid_price | 2 | 5 | 10 |
| 预估收益 | 0.2 | 0.25 | 0.1 |
此时排序为 B,A,C
场景二: 多任务连乘
电商搜索页, 排序表达式是 final_score = ctr * cvr , 所以只看各自的auc有局限, 还得要求二者的数值也尽量准, 这样 final_score 的 auc 才更高.
给一个实际 例子, cvr 纠偏前后, 相对次序不变, 不影响 cvr 任务的 auc, 但能改变最终排序, 影响 ctcvr 任务的auc.

如果样本中 甲是正例, 乙是负例, 那么纠偏后的排序更精准.
以抽象的视角看, 上述两个任务其实是有共性的, 都是 向量相乘中, 一方只改大小不改次序, 却能影响最终排序.
场景三: 数据集负采样
原始数据集的正负样本个数差异过大, 人为增加负样本数量.
这会导致ctr预估偏低, 所以在预测时要对模型预测值进行矫正。
Calibration
(刻度)校准. 应用于场景三. 纠偏公式有解析解, 详见参考 [2].

r 表示负样本的采样比例.
Isotonic regression
保序回归, 详见参考1.
- x x x 表示纠偏前的模型输出
- y ^ \hat y y^ 表示纠偏之后的输出
- y y y 表示后验的真实值.
保序回归就是在满足 任意两个预测值相对大小(保序在这里体现)不变的约束下, 令预测值的偏差尽量小.
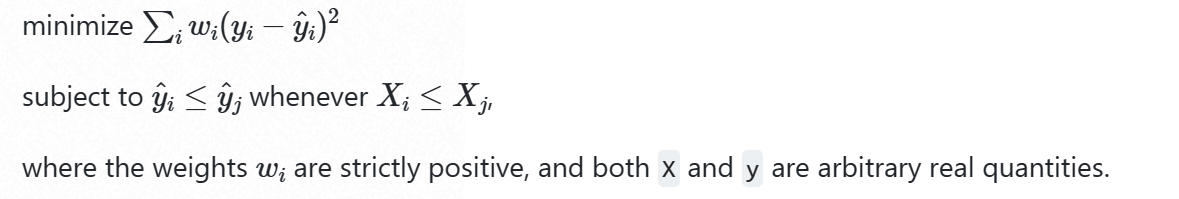
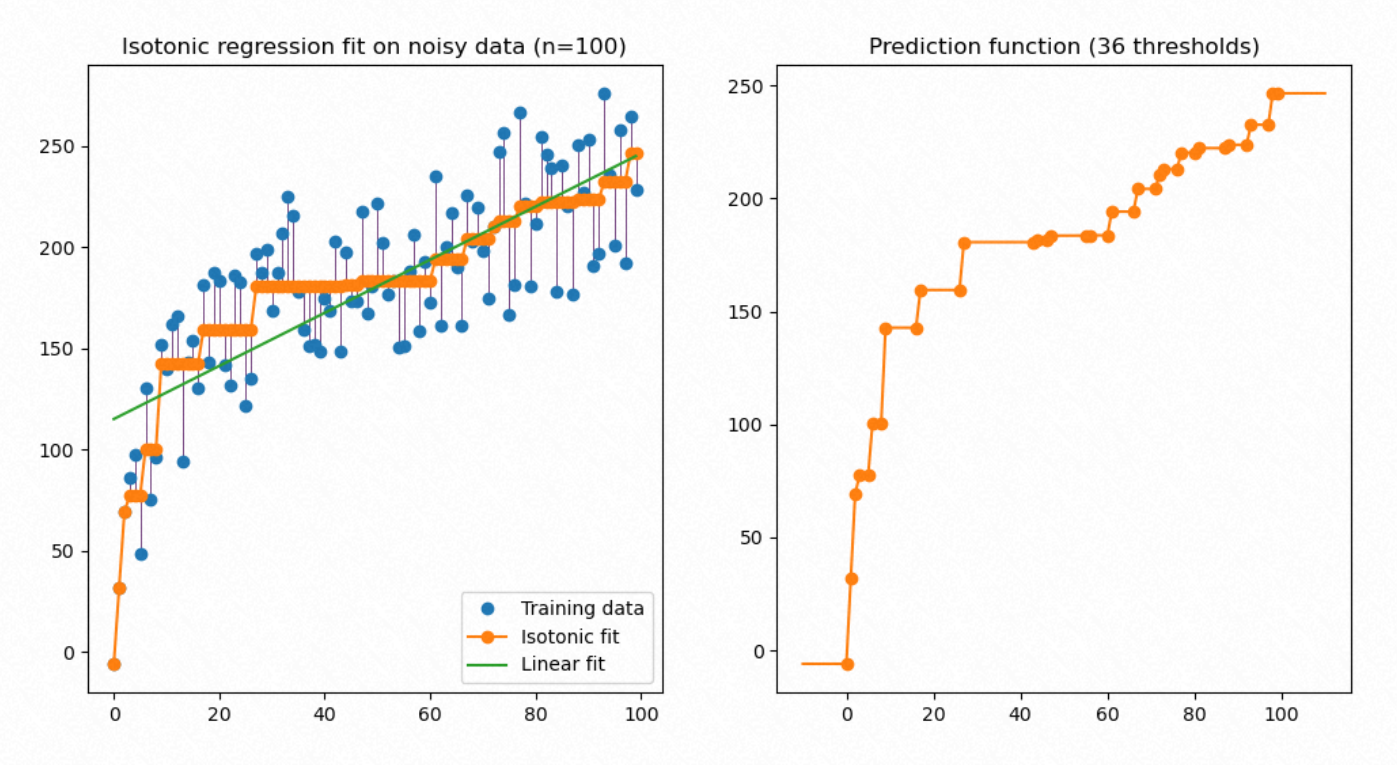
该图来自 sklearn 页面, 因为纠偏后是非递减的, 所以做到了保序.
代码示例:
>>> from sklearn.isotonic import IsotonicRegression
>>> x = [0.1,0.2,0.3,0.4,0.5]
>>> y = [0.3,0.4,0.2,0.0,0.6]
>>> ir = IsotonicRegression()
>>> y_ = ir.fit_transform(x, y)
>>> y_
array([0.225, 0.225, 0.225, 0.225, 0.6 ])
这里有个问题: x,y 也是需要分组计算的, 等距/等频 不同的分组方式, 也会影响纠偏的结果, 那么这里有啥建议呢?
参考
- sklearn-isotonic
- 知乎文章, ctr 先验校准
这篇关于ctr 校准纠偏,保序回归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






