本文主要是介绍经典文献阅读之--Online Extrinsic Camera Calibration for Temporally Consistent IPM (IPM外参标定),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
0. 简介
对于视觉而言,如何使用鸟瞰图来完成车道线的识别和标定是非常重要的,对于鸟瞰图来说,其实有很多种,之前读者的博客中也已经提到过《逆透视变换(IPM)多种方式及代码总结》、《IPM 鸟瞰图公式转换与推导》。这个当然内容还是不太详细,对于各位想要复现难度会比较大,这个时候可以看一下《单应矩阵的推导与理解》这篇文章的详细推导。其实只需要知道精确的外参和内参,以及相机的高度,以及期望的W和H(可以通过视场角(参考1.2公式)和分辨率求得)。而比较难解决的就是外参这类问题。而《Online Extrinsic Camera Calibration for Temporally Consistent IPM Using Lane Boundary Observations with a Lane Width Prior》这个文章就为我们指明了一个比较可行的方法,目前这部分作者已经经过验证,效果还是比较好的。

1. 主要贡献
本文提出了一种对相机的在线外参标定的方法,即在连续的驾驶场景图像中,从路面信息估计俯仰角、偏航角、横滚角和摄像机高度。该方法分两步估计相机的外部参数:
1)利用一组车道线观测值计算的消失点同时估计俯仰角和偏航角;
2)通过最小化车道宽度观测值和车道宽度先验值之间的差异来计算横滚角和摄像机高度。利用扩展卡尔曼滤波(EKF)对摄像机外部参数进行连续更新,最后利用逆透视映射(IPM)生成时间一致的鸟瞰图(BEV)。该文章证明了该方法在合成和真实数据集上的优越性。
2. 消失点求俯仰角和偏航角
消除图像透视投影影响的一个通用方法是使用IPM(逆透视变换),IPM的前提是需要知道相机相对于地面的变换关系,而我们通过标定可以获得相机和车辆之间的变换关系,正常情况下,我们使用固定的外参来进行前视图像和bev图像之间的wrap,但是由于不平整的地面, 车辆运动加减速,上下坡的影响,相机的角度(相对于地面的)会以外参为均值发生变化,我们需要实时的估计出这个变化,从而得到正确的IPM图像。CHENGCHENG GUO的博文就已经比较详细的介绍了这部分的内容。感兴趣的读者可以看一下这篇文章。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5GM65j8I-1680162577703)(https://candyguo.github.io/images/pitch1.png)]
下面我们来看一下这篇文章的方法。在[13]、[15]和[17]中,我们将俯仰角和偏航角估计转化为在路面上平行车道边界的VP与相机之间找到旋转关系,如图3所示。其中 C C C和 W W W分别表示相机和世界坐标系。我们定义 W W W的 z z z轴为VP的方向,即消失方向VD。因此,如图3(b)和图3©所示,俯仰角和偏航角可以定义为相机前方方向与VD之间的夹角。由于车道边界观测结果可能存在噪声,我们采用基于高斯球理论和RANSAC [21]的鲁棒VP估计方法[20]。在使用VP初始化俯仰角和偏航角后,我们通过EKF在连续的图像中对它们进行估计。
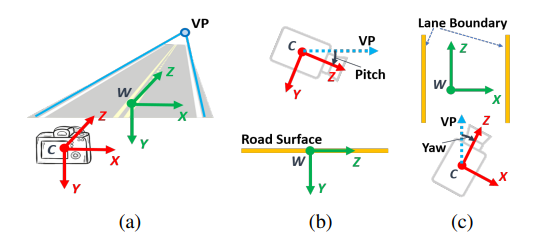
图3:俯仰角和偏航角估计。(a)相机和世界坐标系。(b)和©分别是俯仰角和偏航角的定义。
2.1 高斯球
在针孔相机模型中,以相机主点为中心的单位球称为高斯球。如图4所示,一个大圆是高斯球与由图像上的一条线和主点确定的平面的交点。由于平行线在图像平面上相交于VP,所以对应于平行线的大圆在高斯球上有一个交点,从主点到交点的方向成为VD。VD是由所有大圆(NGCs)法线确定的平面的法向量,我们称之为NGC-VD正交性。 正交性与图像平面中的线-VP的相交是相同的,即图像平面中的平行线与VP相交。
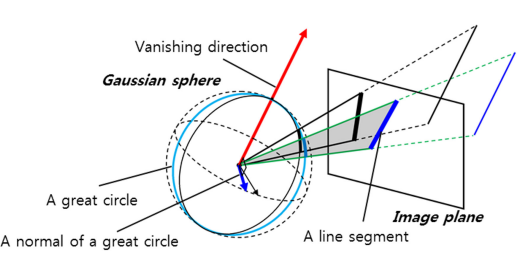
图4:高斯球的描述
3.2 消失点估计
我们假设已经给定了一组表示车道边界的线段。该组通常包含一些噪声线或异常值,因此我们使用RANSAC[21]来过滤掉异常值,然后估计一个对噪声线具有鲁棒性的VP。给定一组线段 L \mathcal{L} L时,RANSAC过程可以描述为算法1。
在算法1中,从两个随机抽样的线段 { l j , l k } ⊂ L \{l_j,l_k\} ⊂ \mathcal{L} {lj,lk}⊂L计算VP假设 v i v_i vi,如下所示:

然后使用Rother [22]的得分函数计算VP假设 v i v_i vi的得分值 s i s_i si。图5显示了计算 s i s_i si时要考虑的两个约束条件:对于每个线段 l ∈ L l ∈ \mathcal{L} l∈L。
1) l l l和包括 v i v_i vi和 l l l的中心点的虚拟线之间的角度 θ ( v i , l ) θ(v_i,l) θ(vi,l)
2) l l l的长度 l l l_l ll。
现在,得分函数定义为:
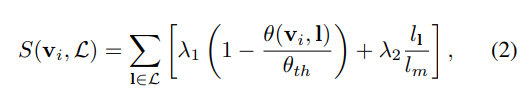

其中, λ 1 λ_1 λ1和 λ 2 λ_2 λ2是权重值,分别设置为0.8和0.2。 θ t h θ_{th} θth是阈值,设置为0.7。 l m l^m lm是 L L L中最长线段的长度。当 θ ( v i , l ) θ(v_i,l) θ(vi,l)不小于 θ t h \theta_{th} θth时,不计算 l l l的得分。因此,通过RANSAC过程对具有最高得分的一组线段 L c Lc Lc行聚类。聚类后的线用于计算最优VP。为了获得最优VP,我们利用第III-A节中提到的NGC-VD正交性。计算每条线 l l l的NGC n n n。
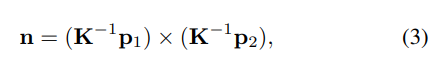
K K K是一个内在相机矩阵, p 1 p_1 p1和 p 2 p_2 p2是l的端点。然后 v v v和NGCs的正交方程为:
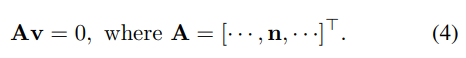
线性方程的超定系统可以通过奇异值分解(SVD)轻松解决。实际上,公式(4)计算出的 v v v是一个被 K K K投影到图像平面上的VD向量,即 v d = K − 1 v p v_d = K^{−1}v_p vd=K−1vp,其中 v d v_d vd和 v p v_p vp分别是VD和VP,但它们是相同的,因此从现在开始VD将被写成VP。
2.3 俯仰角和偏航角的初始化
俯仰角和偏航角分别用 θ θ θ和 φ φ φ表示。通过俯仰角和偏航角计算出的旋转矩阵,即从世界坐标系到相机坐标系的变换矩阵,由 R C W ( θ , φ ) RCW(θ, φ) RCW(θ,φ)表示,世界坐标系 W W W中 z z z轴的方向向量表示为 d W Z = [ 0 , 0 , 1 ] T d_{W_Z}=[0, 0, 1]^T dWZ=[0,0,1]T。然后 d W Z d_{W_Z} dWZ和 v v v有以下关系
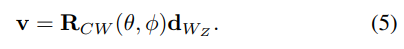
我们可以将旋转矩阵分解为 θ θ θ和 φ φ φ的两个旋转矩阵,如下所示。
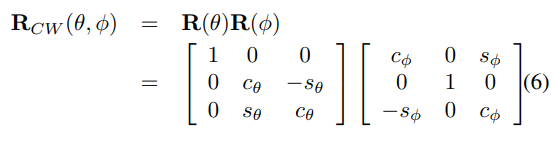
其中 c θ c_θ cθ和 s θ s_θ sθ( c φ c_φ cφ和 s φ s_φ sφ)是 θ ( φ ) θ(φ) θ(φ)的余弦和正弦函数值。然后,从 v v v中初始化 θ θ θ和 φ φ φ,如下所示。
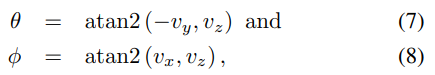
这里的 v = [ v x , v y , v z ] v = [v_x, v_y, v_z] v=[vx,vy,vz],而 a t a n 2 ( y , x ) atan2(y, x) atan2(y,x)是双参数反正切函数。
2.4 通过EKF估计俯仰角和偏航角
我们采用EKF [18]来估计图像序列中的俯仰角和偏航角。在驾驶过程中,采用恒定角速度模型来建立俯仰角和偏航角变化的模型。因此,定义了一个状态向量 x P Y x_{PY} xPY和一个系统模型 f P Y f_{PY} fPY来进行俯仰角和偏航角的估计:
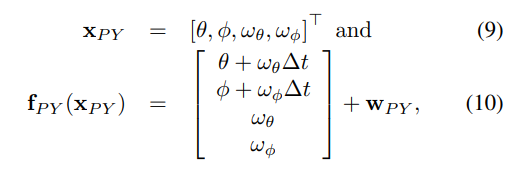
其中 ω θ ω_θ ωθ和 ω φ ω_φ ωφ是俯仰角和偏航角的角速度, w P Y = [ 0 , 0 , w θ , w φ ] T w_{PY} = [0, 0, w_θ, w_φ]^T wPY=[0,0,wθ,wφ]T是带有正态分布 N ( 0 , W P Y ) N(0,W_{PY}) N(0,WPY)的系统模型噪声变量。
利用NGC-VD正交性,定义了一个用于俯仰角和偏航角估计的测量模型 h P Y h_{PY} hPY。
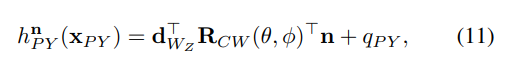
其中 n n n是 I ∈ L c I\in \mathcal{L}_c I∈Lc中的NGC, q P Y q_{PY} qPY是测量模型的噪声变量,其正态分布为 N ( 0 , Q P Y ) N(0,Q_{PY}) N(0,QPY)时。 EKF通过以下方式估计状态向量 x P Y x_{PY} xPY:
…详情请参照古月居
这篇关于经典文献阅读之--Online Extrinsic Camera Calibration for Temporally Consistent IPM (IPM外参标定)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









