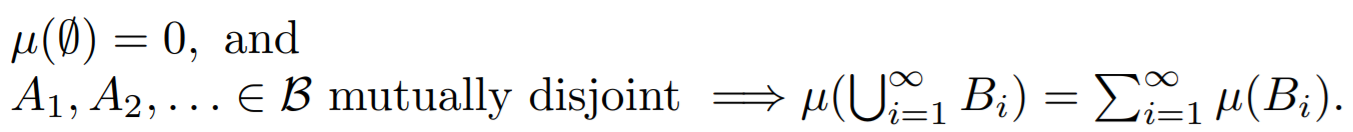Borel-Cantelli 引理

本文主要是介绍Borel-Cantelli 引理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

翻译自大佬
https://huarui1998.com/Notes/math/borel-cantelli.html

1. 集序列的 $\lim \inf$ 和 $\lim \sup$

类似于定义实数序列 { a k } \{a_k\} {ak​} 的 $\lim \inf$ 和 $\lim \sup$,
$$\underset{k\to \infty }{\mathrm{liminf}}{a}_k=\underset{n\ge 1}{\sup }(\underset{k\ge n}{\inf }{a}_k),\underset{k\to \infty }{\mathrm{limsup}}{a}_k=\underset{n\ge 1}{\inf }(\underset{k\ge n}{\sup }{a}_k),$$
我们也可以定义集序列 { A k } \{A_k\} {Ak​} 的 $\lim \inf$ 和 $\lim \sup$,
只需将 $\inf$ 替换为 $\cap$，将 $\sup$ 替换为 $\cup$，即
$$\underset{k\to \infty }{\mathrm{liminf}}{A}_k=\bigcup _{n\ge 1}\bigcap _{k\ge n}{A}_k,\underset{k\to \infty }{\mathrm{limsup}}{A}_k=\bigcap _{n\ge 1}\bigcup _{k\ge n}{A}_k.$$
根据德摩根定律，我们有
$${\left(\underset{k\to \infty }{\mathrm{limsup}}{A}_k\right)}^c={\left(\bigcap _{n\ge 1}\bigcup _{k\ge n}{A}_k\right)}^c=\bigcup _{n\ge 1}{\left(\bigcup _{k\ge n}{A}_k\right)}^c=\bigcup _{n\ge 1}\bigcap _{k\ge n}{A}_k^c=\underset{k\to \infty }{\mathrm{liminf}}{A}_k^c.\text{\hspace{1em}(1)}$$

这两个符号有两个重要性质。

定理

1. $a\in \lim \underset{k}{\inf }{A}_k$ 当且仅当存在一个整数 $N$ 使得 $a\in A_n$ 对所有 $n\ge N$ 成立。
2. $a\in \lim \underset{k}{\sup }{A}_k$ 当且仅当 $a$ 属于 { A k } \{A_k\} {Ak​} 的无穷多个项。

证明

首先，如果 $a\in {\mathrm{liminf}}_k{A}_k$，这意味着 $a$ 属于 { ∩ k ≥ n A k : n ≥ 1 } \{\cap_{k\geq n}A_k:n\geq 1\} {∩k≥n​Ak​:n≥1} 中的至少一个，假设 $a\in {\cap }_{k\ge N}{A}_k$，
那么 $a\in A_k$ 对所有 $k\ge N$ 成立。

其次，如果 $a\in {\mathrm{limsup}}_k{A}_k$，这意味着 $a$ 属于 { ∪ k ≥ n A k : n ≥ 1 } \{\cup_{k\geq n}A_k:n\geq 1\} {∪k≥n​Ak​:n≥1} 的所有。
假设 $a$ 只属于 { A k } \{A_k\} {Ak​} 的有限项，例如 { A k 1 , ⋯ , A k m } \{A_{k_1},\cdots,A_{k_m}\} {Ak1​​,⋯,Akm​​}，那么令 M = max ⁡ { k 1 , ⋯ , k m } M = \max\{k_1,\cdots,k_m\} M=max{k1​,⋯,km​}，我们有
$a\notin A_k$ 对所有 $k\ge M+1$ 成立，即 $a\notin {\cup }_{k\ge M+1}{A}_k$，这导致矛盾。
$$\text{\hspace{1em}■}$$

由于上述定理，有时我们说事件 $A_k$ ($k=1,2,\cdots$) 无穷次发生，如果事件 ${\mathrm{limsup}}_k{A}_k$ 发生，或简称为 $A_k$ i.o.。

定理

如果每个 $A_k$ 是一个事件（即 $\in \mathcal{F}$），我们有

1. $$\mathbb{P}(\underset{k\to \infty }{\mathrm{liminf}}{A}_k)=\underset{n\to \infty }{\lim }\mathbb{P}(\bigcap _{k\ge n}{A}_k)\text{\hspace{1em}(2)}$$
2. $$\mathbb{P}(\underset{k\to \infty }{\mathrm{limsup}}{A}_k)=\underset{n\to \infty }{\lim }\mathbb{P}(\bigcup _{k\ge n}{A}_k)\text{\hspace{1em}(3)}$$

证明

记
$$F_n=\bigcap _{k\ge n}{A}_k,$$
那么 { F n } \{F_n\} {Fn​} 是一个递增序列，即 $F_1\subseteq F_2\subseteq F_3\cdots$，根据概率测度的连续性，我们有
$$\mathbb{P}(\bigcup _n{F}_n)=\underset{n\to \infty }{\lim }\mathbb{P}(F_n),$$
因此 (2) 成立。 (3) 也直接由 (1) 和 (2) 得出。
$$\text{\hspace{1em}■}$$

2. 第一 Borel-Cantelli 引理

定理（Borel-Cantelli）

假设 { A k } \{A_k\} {Ak​} 是事件，如果
$$\sum _k\mathbb{P}(A_k)<\infty ,$$
那么我们有 $$\mathbb{P}(A_k\text{i.o.})=0.$$

证明

记 $B_n$ 为 $$B_n=\bigcup _{k\ge n}{A}_k,$$
根据 (3) 我们有
$$\mathbb{P}(A_k\text{i.o.})=\mathbb{P}(\underset{k\to \infty }{\mathrm{limsup}}{A}_k)=\underset{n\to \infty }{\lim }\mathbb{P}(B_n).$$
我们只需要证明 $\mathbb{P}(B_n)\to 0$。
由于概率测度的次可加性，我们有
$$\mathbb{P}(B_n)=\mathbb{P}(\bigcup _{k\ge n}{A}_k)\le \sum _{k=n}^{\infty }\mathbb{P}(A_k)=\sum _{k=1}^{\infty }\mathbb{P}(A_k)-\sum _{k=1}^{n-1}\mathbb{P}(A_k)\to 0,$$
当 $n\to \infty$ 时，收敛性由
$$\sum _{k=1}^{\infty }\mathbb{P}(A_k)<\infty$$ 保证。

$$\text{\hspace{1em}■}$$

3. 第二 Borel-Cantelli 引理

定理（Borel-Cantelli）

假设 { A k } \{A_k\} {Ak​} 是独立事件，如果
$$\sum _k\mathbb{P}(A_k)=\infty ,$$
那么我们有 $$\mathbb{P}(A_k\text{i.o.})=1.$$

证明

根据(1)，我们有：
$$\begin{array}{rlr}\mathbb{P}(A_k\text{i.o.})& =\mathbb{P}(\underset{k\to \infty }{\mathrm{limsup}}{A}_k)& \\ & =1-\mathbb{P}(\underset{k\to \infty }{\mathrm{liminf}}{A}_k^c)& \\ & =1-\underset{n\to \infty }{\lim }\mathbb{P}\left(\bigcap _{k\ge n}{A}_k^c\right)& \text{(根据 (2))}\\ & =1-\underset{n\to \infty }{\lim }\prod _{k=n}^{\infty }\mathbb{P}(A_k^c)& \text{(由于独立性)}\\ & =1-\underset{n\to \infty }{\lim }\prod _{k=n}^{\infty }(1-\mathbb{P}(A_k))& \\ & \ge 1-\underset{n\to \infty }{\lim }\prod _{k=n}^{\infty }\exp (-\mathbb{P}(A_k))& \text{(因为 1−x≤e−x)}\\ & =1-\underset{n\to \infty }{\lim }\exp \left(-\sum _{k=n}^{\infty }\mathbb{P}(A_k)\right)& \\ & =1& \text{(因为对于任何 n，∑k=n∞P(Ak)=∞)}\end{array}$$
\tag*{$■$}

我们可以通过将“独立”替换为一个更弱的条件“成对独立”来增强第二 Borel-Cantelli 引理。

定理（成对独立版本 Borel-Cantelli 引理）

假设 { A k } \{A_k\} {Ak​} 是成对独立事件，如果
$$\sum _k\mathbb{P}(A_k)=\infty ,$$
那么我们有 $$\mathbb{P}(A_k\text{i.o.})=1.$$

证明

设 ${\mathbb{I}}_k$ 为 $A_k$ 的指示函数，则 $\mathbb{E}({\mathbb{I}}_k)=\mathbb{P}(A_k)$。设 $S_n$ 为 ${\mathbb{I}}_k$ 的部分和，即
$$S_n=\sum _{k=1}^n{\mathbb{I}}_k,$$
记
$$S=\underset{n\to \infty }{\lim }{S}_n=\sum _{k=1}^{\infty }{\mathbb{I}}_k.$$
那么 ${\sum }_k\mathbb{P}(A_k)=\infty$ 意味着
$$\mathbb{E}(S)=\infty .$$
而 $x\in A_k\text{i.o.}$ 等价于
$$S(x)=\sum _{k=1}^{\infty }{\mathbb{I}}_k(x)=\infty ,$$
因此我们的目标是证明 $\mathbb{P}(S=\infty )=1$。记 $p_k=\mathbb{P}(A_k)$，则 $S_n$ 的方差为
$$\begin{array}{rl}Var(S_n)& =\mathbb{E}(S_n^2)-[\mathbb{E}(S_n){]}^2\\ & =\mathbb{E}\left(\sum _{k=1}^n{\mathbb{I}}_k^2+\sum _{i\ne j}{\mathbb{I}}_i{\mathbb{I}}_j\right)-{\left(\sum _{k=1}^n{p}_k\right)}^2\\ & =\sum _{k=1}^n\mathbb{E}({\mathbb{I}}_k^2)+\sum _{i\ne j}\mathbb{E}({\mathbb{I}}_i)\mathbb{E}({\mathbb{I}}_j)-{\left(\sum _{k=1}^n{p}_k\right)}^2\\ & =\sum _{k=1}^n{p}_k+\sum _{i\ne j}{p}_i{p}_j-{\left(\sum _{k=1}^n{p}_k\right)}^2\\ & =\sum _{k=1}^n{p}_k+{\left(\sum _{k=1}^n{p}_k\right)}^2-\sum _{k=1}^n{p}_k^2-{\left(\sum _{k=1}^n{p}_k\right)}^2\\ & =\sum _{k=1}^n(p_k-p_k^2)\\ & \le \mathbb{E}(S_n)\end{array}$$

然后，
$$\begin{array}{rl}\mathbb{P}\left(S<\frac{\mathbb{E}(S_n)}{2}\right)& \le \mathbb{P}\left(S_n<\frac{\mathbb{E}(S_n)}{2}\right)\\ & =\mathbb{P}\left(S_n-\mathbb{E}(S_n)<-\frac{\mathbb{E}(S_n)}{2}\right)\\ & \le \mathbb{P}\left(\left|S_n-\mathbb{E}(S_n)\right|\ge \frac{\mathbb{E}(S_n)}{2}\right)\\ & \le \frac{4Var(S_n)}{[\mathbb{E}(S_n){]}^2}(\text{由切比雪夫不等式})\\ & \le \frac{4}{\mathbb{E}(S_n)}(\text{因为 Var(Sn)≤E(Sn)})\end{array}\text{\hspace{1em}(4)}$$
注意 { S < E ( S n ) 2 } \{S < \frac{\mathbb{E}(S_n)}{2}\} {S<2E(Sn​)​} 上升到 { S < ∞ } \{S < \infty\} {S<∞}，最后通过概率测度的连续性，
P ( S < ∞ ) = P ( ⋃ n = 1 ∞ { S < E ( S n ) 2 } ) = lim ⁡ n → ∞ P ( S < E ( S n ) 2 ) ≤ lim ⁡ n → ∞ 4 E ( S n ) = 0 , \mathbb{P}(S < \infty) = \mathbb{P}\left(\bigcup_{n=1}^\infty \{S < \frac{\mathbb{E}(S_n)}{2}\}\right) = \lim_{n \to \infty} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right) \leq \lim_{n \to \infty} \frac{4}{\mathbb{E}(S_n)} = 0, P(S<∞)=P(n=1⋃∞​{S<2E(Sn​)​})=n→∞lim​P(S<2E(Sn​)​)≤n→∞lim​E(Sn​)4​=0,
那么我们得出
$$\mathbb{P}(S=\infty )=1-\mathbb{P}(S<\infty )=1.$$
$$\text{\hspace{1em}■}$$

4. Erdös-Rényi 定理

上述定理中的成对独立条件可以进一步放宽，得到 Erdös-Rényi 定理。

定理（Erdös-Rényi）

假设 { A k } \{A_k\} {Ak​} 是事件，如果
$$\sum _k\mathbb{P}(A_k)=\infty ,$$
并且
$$\underset{n\to \infty }{\mathrm{liminf}}\frac{{\sum }_{j=1}^n{\sum }_{k=1}^n\mathbb{P}(A_j\cap A_k)}{{\left({\sum }_{k=1}^n\mathbb{P}(A_k)\right)}^2}=1,\text{\hspace{1em}(5)}$$
那么我们有
$$\mathbb{P}(A_k\text{i.o.})=1.$$

证明

我们将使用与之前相同的记号 $S_n$ 和 $S$。因为
$$\mathbb{E}(S_n^2)=\mathbb{E}\left[{\left(\sum _{k=1}^n{\mathbb{I}}_k\right)}^2\right]=\sum _{j,k=1}^n\mathbb{E}({\mathbb{I}}_j{\mathbb{I}}_k)=\sum _{j,k=1}^n\mathbb{P}(A_j\cap A_k),$$
并且
$$\mathbb{E}(S_n)=\sum _{k=1}^n\mathbb{P}(A_k),$$
因此 (5) 等价于
$$\underset{n\to \infty }{\mathrm{liminf}}\frac{\mathbb{E}(S_n^2)}{[\mathbb{E}(S_n){]}^2}=1。$$
根据 (4) 的前四行，我们有
$$\mathbb{P}\left(S<\frac{\mathbb{E}(S_n)}{2}\right)\le 4\frac{\mathbb{E}(S_n^2)-[\mathbb{E}(S_n){]}^2}{[\mathbb{E}(S_n){]}^2}=4\left(\frac{\mathbb{E}(S_n^2)}{[\mathbb{E}(S_n){]}^2}-1\right),$$
然后我们有
P ( S < ∞ ) = P ( ⋃ n = 1 ∞ { S < E ( S n ) 2 } ) = lim ⁡ n → ∞ P ( S < E ( S n ) 2 ) ( 因为  { S < E ( S n ) 2 } 递增，且根据单调收敛定理 ) = lim inf ⁡ n → ∞ P ( S < E ( S n ) 2 ) ( 因为最后极限由单调收敛定理存在 ) ≤ 4 ( lim inf ⁡ n → ∞ E ( S n 2 ) [ E ( S n ) ] 2 − 1 ) = 0 , \begin{aligned} \mathbb{P}(S < \infty) &= \mathbb{P}\left(\bigcup_{n=1}^\infty \{S < \frac{\mathbb{E}(S_n)}{2}\}\right) \\ &= \lim_{n \to \infty} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right)\quad (\text{因为 $\{S < \frac{\mathbb{E}(S_n)}{2}\}$ 递增，且根据单调收敛定理}) \\ &= \liminf_{n \to \infty} \mathbb{P}\left(S < \frac{\mathbb{E}(S_n)}{2}\right)\quad (\text{因为最后极限由单调收敛定理存在}) \\ &\leq 4\left(\liminf_{n \to \infty} \frac{\mathbb{E}(S^2_n)}{[\mathbb{E}(S_n)]^2} - 1\right) = 0, \end{aligned} P(S<∞)​=P(n=1⋃∞​{S<2E(Sn​)​})=n→∞lim​P(S<2E(Sn​)​)(因为 {S<2E(Sn​)​} 递增，且根据单调收敛定理)=n→∞liminf​P(S<2E(Sn​)​)(因为最后极限由单调收敛定理存在)≤4(n→∞liminf​[E(Sn​)]2E(Sn2​)​−1)=0,​
这表明
$$\mathbb{P}(S=\infty )=1-\mathbb{P}(S<\infty )=1.$$
$$\text{\hspace{1em}■}$$

参考文献

1. Kai Lai Chung, A Course in Probability Theory, 第三版 (2001)
2. Rick Durrett, Probability: Theory and Examples, 第五版 (2019)

这篇关于Borel-Cantelli 引理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---