引理专题
Borel-Cantelli 引理
翻译自大佬 https://huarui1998.com/Notes/math/borel-cantelli.html 1. 集序列的 lim inf \lim\inf liminf 和 lim sup \lim\sup limsup 类似于定义实数序列 { a k } \{a_k\} {ak} 的 lim inf \lim\inf liminf 和 lim
数学分析复习:黎曼引理、黎曼-勒贝格引理
文章目录 黎曼引理、黎曼-勒贝格引理Riemann引理Riemann-Lebesgue引理 本篇文章适合个人复习翻阅,不建议新手入门使用 黎曼引理、黎曼-勒贝格引理 Riemann引理 我们知道一般情况下积分算子是无法保持乘法的,即 ∫ a b f ( x ) ⋅ g ( x ) d x ≠ ∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x
【抽代复习笔记】13-群(七):变换群引理
引理:考虑等边三角形123—— 这个等边三角形的对称性可用(1),(12),(13),(23),(123),(132)表示,其中: (1)表示这个等边三角形绕着其中心点旋转360°/720°/.../360°×n,得到的图形与原图形完全重合的旋转对称变换; (12)表示这个等边三角形绕过点3、垂直于边12的对称轴翻转180°/540°/.../180°+360°×n,得到的图形与原图形相
组合数学常用内容——Polya定理+Burnside引理
Burnside引理 设G是N{1,2,.....,n}上的置换群,G在N上可引出不同的等价类(在置换群中有置换的都等价),其不同的等价类的个数为LL=1/|G|*(c1(a1)+...c1(ai)...+c1(ag))c1表示置换ai作用过后不变的方案数,也就是置换中循环节长度是1的循环个数(N中的元素是组合方案的序号不是自然数!此置换群是关于所有着色图像(所有可能的情况)集合N的置换)Bur
Cells(2021牛客暑期多校训练营9 C,LGV引理 + 范德蒙德行列式 + NTT)
一、题目链接 Cells 二、题目大意 在一个二维平面内,有 n n n 个起点 ( 0 , a i ) (0, a_i) (0,ai) 要走到对应的终点 ( i , 0 ) (i, 0) (i,0),每次可以向下走或向左走,问不相交路径组的方案数. 1 ≤ n ≤ 5 × 1 0 5 , 0 ≤ a i ≤ 1 0 6 , a i < a i + 1 1 \leq n \leq
图与网络——图染色中的Sperner引理
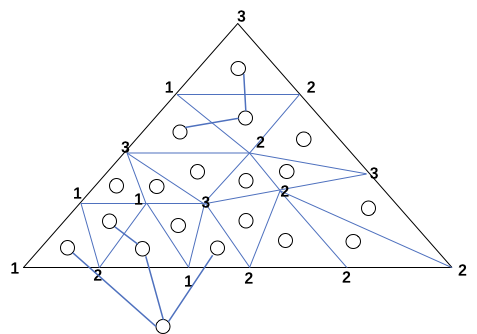
问题背景: 将一个大的三角形三角形化,然后用三种颜色染色,三个大的顶点分别染1,2,3颜色,且边上的点只能染1,2颜色,其他两条边类似,中间的点可以染任意颜色,则一定存在满足三个顶点分别是三种不同颜色的小三角形。 举例: 证明方法1: 对三角形中异色边进行计数,假如没有满足条件的小三角形,异色边的数目应该是偶数;但是在大三角形中,三条边上的异色变的数目一定是奇数,和也是奇数,内部的
一些笔记自己备忘,魔方最少步数的起点:Thistlethwaite‘s algorithm算法的引理。
前置: 1. w : 是一个映射,(但是不满足同态性质),类型是:H→ C2^(12), w(g)第i个分量wi表示: 在第i位置的原坐标下,按逆时针计算的方向数为Fi,这个棱块x,经过某{F,B,L,R,U,D}某复合一个操作后,到达了第j位置 在新的第j位置的坐标下,按逆时针计算的方向数Fj,则这两个数之间的关系是:(Fi + wi) 再mod 3 , 就等于 Fj。也就是Fi+wi=F
@总结 - 12@ burnside引理与pólya定理
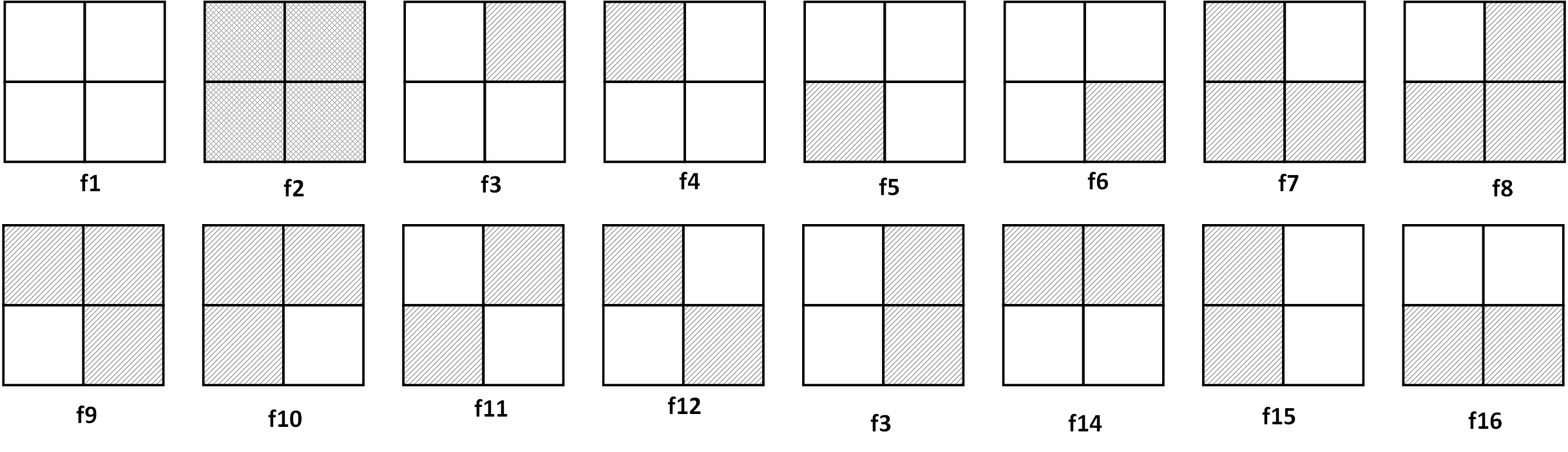
目录 @0 - 参考资料@@1 - 问题引入@@2 - burnside引理@@3 - pólya定理@@4 - pólya定理的生成函数形式@ @0 - 参考资料@ 博客1 @1 - 问题引入@ 一个经典问题: 一正方形分成4格,2着色,有多少种方案? 其中,经过转动相同的图象算同一方案。 假如不考虑转动,各种方案如下所示。 首先可以发现,转动的角度只有 4 种:0°,90°,180
对acwing355异象石引理的证明
首先我们抽象一下这道题的模型,然后把引理记住 模型:对于一棵树上选定的一些点,把他们连通起来的最小边数 我们先考虑一种朴素做法,对于任何一种方案,任取其中两个点,那么这个方案一定包含这两个点之间的路径 就是说,我们依次添加每个点,对于每一个新添加进来的点,让这个点与其已经添加的点求路径,然后把路径上每条边染色一次,最后有多少条边被染色就证明这些边都是必须要要的,另一方面,把这些边选上一定连通,所
埃舍尔的绘画与Zorn引理
我以前写过博文埃舍尔的绘画,自指,以及罗素悖论.在那篇博文里,我探讨了埃舍尔的绘画与正则公理的关系.现在我来探讨一下埃舍尔的绘画与Zorn引理的关系.再次以下面的图片为例. 转载于:https://www.cnblogs.com/yeluqing/archive/2013/01/26/3827839.html
名词解释----------命题、定理、推论、引理
1. 命题 在现代哲学、数学、逻辑学、语言学中,命题是指一个判断(陈述)的语句(实际表达的概念),这个概念是可以被定义并观察的现象。命题不是指判断(陈述)本身,而是指所表达的语义。但相异判断(陈述)具有相同语义的时候,它们表达相同的命题。 在数学中,一般把判断某一事情的陈述句叫做命题。 The term proposition has a broad use in contemporary
「管理数学基础」3.1 凸分析:凸集与凸集分离定理、Farkas引理
凸集与凸集分离定理、Farkas引理 文章目录 凸集与凸集分离定理、Farkas引理凸集定义:凸集凸集性质(逐个证明) 超平面定义:超平面证明:超平面是凸集定义:支撑超平面定义:多面体定义:凸锥 凸集分离定理定义:分离定义:凸集分离定理 Farkas引理定义:Farkas引理证明:Farkas引理 凸集 定义:凸集 注意凸集的定义,任取两点满足某个条件为凸集: 证明
latex 定理环境,引理,定义,自定义 proof 环境
l一般的atex 的定理环境, amsmath 安装包自带,用法为: \newtheorem {环境名} {标题} [排序单位] [排序单位] 一般为 chapter,若带上 chapter 则表示 定理按章节编号。 下列代码放入导言区: \usepackage{amsmath}\newtheorem{theorem}{Theorem}\newtheorem{lemma}
【计算理论】泵引理以及应用(证明某些语言不是正则的)
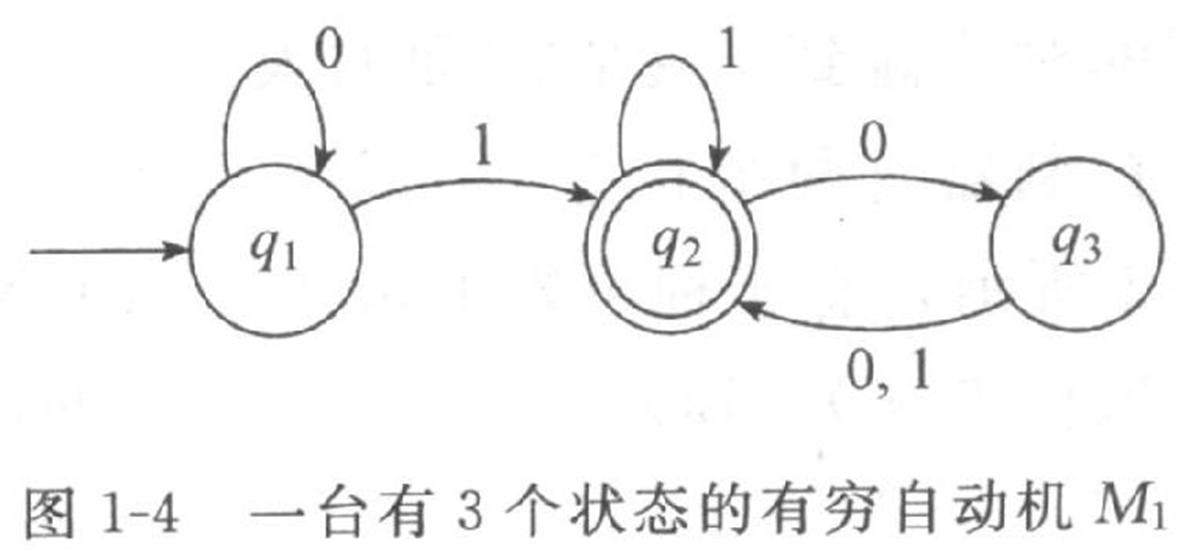
2019独角兽企业重金招聘Python工程师标准>>> 1、基础知识 1.1、一个典型的有穷自动机状态图 状态:q1;q2;q3起始状态q1用一个指向它的无出发点的箭头表示;接受状态q2带有双圈转移:从一个状态指向另一个状态的箭头 本例中q1为起始状态,q2为接受状态。如果一个字符串w经过M1可以到达接受状态那称为M1接受s(比如字符串1,01,001,0011等等会被M1接受