本文主要是介绍图与网络——图染色中的Sperner引理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题背景:
将一个大的三角形三角形化,然后用三种颜色染色,三个大的顶点分别染1,2,3颜色,且边
上的点只能染1,2颜色,其他两条边类似,中间的点可以染任意颜色,则一定存在满足三个顶点分别是三种不同颜色的小三角形。
举例:

证明方法1:
对三角形中异色边进行计数,假如没有满足条件的小三角形,异色边的数目应该是偶数;但是在大三角形中,三条边上的异色变的数目一定是奇数,和也是奇数,内部的边因为会被计数两次,一定是偶数,则总的异色边的数目是奇数,推出矛盾。
证明方法2:
每个三角形内部造一个顶点,三角形外一个点,只连会经过(1,2)边的两个点,外部的点一定是奇度点,由于图中奇度点的个数是偶数个,则还有奇数个奇度点。
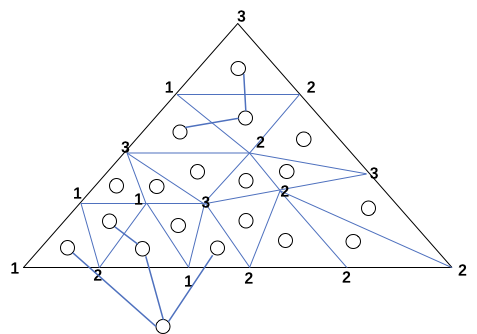
这篇关于图与网络——图染色中的Sperner引理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







