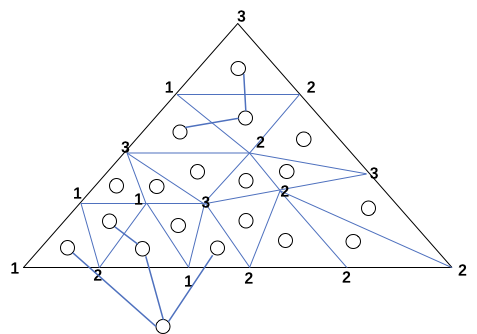
问题背景： 将一个大的三角形三角形化，然后用三种颜色染色，三个大的顶点分别染1，2，3颜色，且边上的点只能染1，2颜色，其他两条边类似，中间的点可以染任意颜色，则一定存在满足三个顶点分别是三种不同颜色的小三角形。 举例： 证明方法1: 对三角形中异色边进行计数，假如没有满足条件的小三角形，异色边的数目应该是偶数；但是在大三角形中，三条边上的异色变的数目一定是奇数，和也是奇数，内部的

Sperner定理及其证明 额，最近看到了一个十分有趣的定理——Sperner定理。其实这个定理在OI中没什么用处，因此我都没把这篇文章放到我的OI标签里(不知道在MO中是否有用？)但是觉得它很有趣于是就过来写一下。 由于博主太弱不会用LaTeX写取整符号，本文中用\([x]\)表示\(x\)下取整。 问题: 有一个\(n\)元集合\(S_n\)，从中选出若干个子集，满足没有任何两个子集

额，最近看到了一个十分有趣的定理——Sperner定理。其实这个定理在OI中没什么用处，因此我都没把这篇文章放到我的OI标签里(不知道在MO中是否有用？)但是觉得它很有趣于是就过来写一下。 由于博主太弱不会用LaTeX写取整符号，本文中用\([x]\)表示\(x\)下取整。 问题: 有一个\(n\)元集合\(S_n\)，从中选出若干个子集，满足没有任何两个子集之间存在包含关系，问最多能选出多少个

爱学习，勤思考；学数学，玩魔术。欢迎点击头部蓝字关注MatheMagician，这里有你要的奇迹！ 终于来到本系列的最后一篇！   在前面三期文章中，我们就《字母预言卡》这个魔术所包含的表演技巧和背后的数学模型的分析和完整建模给大家作了阐述。相关内容回顾如下：     这里再放一下对应魔术的表演视频：   视频1 字母预言卡   以及数学建模对这个魔术背后的数学转化：   给定m个元素