首先我们抽象一下这道题的模型,然后把引理记住
模型:对于一棵树上选定的一些点,把他们连通起来的最小边数
我们先考虑一种朴素做法,对于任何一种方案,任取其中两个点,那么这个方案一定包含这两个点之间的路径
就是说,我们依次添加每个点,对于每一个新添加进来的点,让这个点与其已经添加的点求路径,然后把路径上每条边染色一次,最后有多少条边被染色就证明这些边都是必须要要的,另一方面,把这些边选上一定连通,所以最小的方案是唯一的
下面证明引理
首先,对于两个点,引理显然成立
假设对于n个点的时候引理成立,下面证明n+1个点的时候引理也成立
我们这么考虑这n+1个点,添加顺序是按照各个点的dfn顺序来添加的,所以最后一个添加的点一定是dfn最大的
假设第n+1个点是第n个点的子节点,那么此时我们已经添加完n个点的时候,根据朴素做法,我们选的边是唯一的,加入第n+1个点时,我们计算其余点与这个第n+1的点的路径时,一定都是第n+1号点先到第n号点,然后再从第n号点到其他点,然而从第n号点到其他点的路径已经都被染色了,就没必要考虑了,所以最后新的被染色的边就是第n+1号点先到第n号点这条路径,稍微计算就可以知道引理成立
假设第n+1个点不是第n个点的子节点,那么见下图
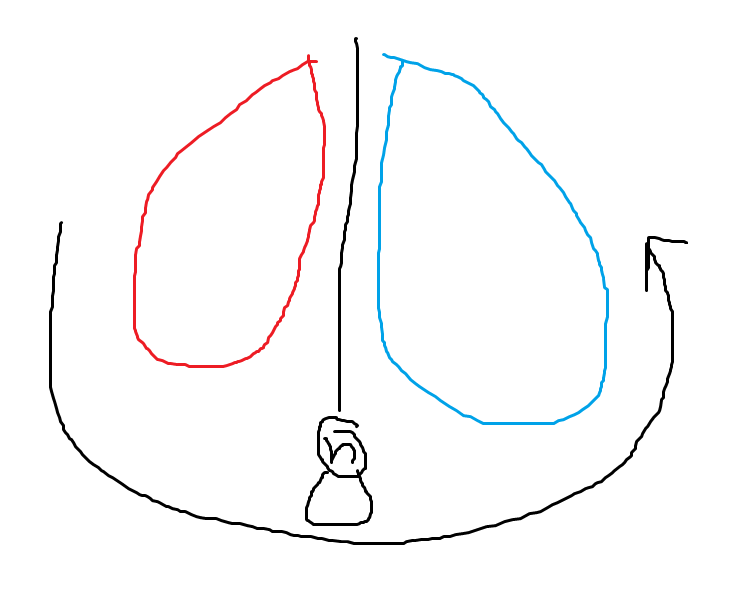
访问dfn一定是先访问红色部分,在访问n及其子树,再访问蓝色部分
而且红色部分是从上往下,蓝色部分是从下往上
那么此时第n+1号节点只能在蓝色部分,那么按照第n+1个点是第n个点的子节点的方法进行计算也会发现引理成立
综上,引理证毕







