【机器学习聚类算法实战-5】机器学习聚类算法之DBSCAN聚类、K均值聚类算法、分层聚类和不同度量的聚集聚类实例分析

本文主要是介绍【机器学习聚类算法实战-5】机器学习聚类算法之DBSCAN聚类、K均值聚类算法、分层聚类和不同度量的聚集聚类实例分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🎩 欢迎来到技术探索的奇幻世界👨‍💻

📜 个人主页：@一伦明悦-CSDN博客

✍🏻 作者简介： C++软件开发、Python机器学习爱好者

🗣️ 互动与支持：💬评论 👍🏻点赞 📂收藏 👀关注+

如果文章有所帮助，欢迎留下您宝贵的评论，

点赞加收藏支持我，点击关注，一起进步！

前言

正文

01- DBSCAN聚类算法简介

02- 基于K均值的颜色量化实战

03- 分层聚类：结构化区域与非结构化区域

04- 不同度量的聚集聚类实战

总结

前言

          DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法是一种基于密度的聚类算法，能够有效地发现任意形状的聚类，并能够处理噪声数据。该算法通过定义特定半径内的数据点数量来构建具有足够密度的聚类，并将稀疏区域或孤立点识别为噪声。DBSCAN算法的优势在于无需指定聚类数目，适用于各种数据形状和大小的数据集。

        K均值聚类算法是一种基于距离的聚类算法，将数据点分为K个簇以最小化每个簇内数据点到簇中心的距离平方和。该算法需要提前指定簇的数量K，并通过随机初始化簇中心和迭代更新样本的簇分配来进行聚类。K均值聚类算法的优势在于简单易理解、实现方便，但对初始质心敏感，且对异常值敏感。

        分层聚类是一种层次化的聚类方法，根据数据间的相似性逐步合并聚类簇，形成一个完整的聚类层次结构。分层聚类方法包括凝聚聚类（agglomerative clustering）和分裂聚类（divisive clustering）两种主要策略。凝聚聚类从单个样本开始，逐步合并最相似的聚类，形成一个树状结构；分裂聚类则从一个包含所有样本的聚类开始，逐步分裂为子聚类。分层聚类的优势在于可以同时得到不同层次的聚类结果，帮助分析数据的聚类结构。

        不同度量的聚集实例分析包括了选择不同的距离度量或相似性度量来计算数据点之间的距离，并应用于聚类算法中。常用的距离度量包括欧氏距离、曼哈顿距离、余弦相似度等，不同的度量方式会影响聚类结果的质量和形状。选择合适的度量方式对于聚类算法的效果至关重要，需要根据具体数据的特点和问题需求进行选择。例如，在处理图像数据时，可以选择使用像素之间的欧氏距离；在自然语言处理领域，可以选择余弦相似度度量文本之间的相似性。通过实例分析不同度量方式在聚类任务中的应用，可以更好地理解数据间的相似性和差异性，提高聚类算法的效果和准确性。

正文

01- DBSCAN聚类算法简介

          DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法是一种基于密度的聚类算法，能够有效地发现任意形状的聚类，并可以处理噪声数据。下面是对DBSCAN聚类算法的详细分析，包括原理和步骤：

        原理分析：

        DBSCAN算法基于以下两个重要概念来实现聚类：

         核心对象（Core Point）：如果一个数据点的邻域内至少包含指定数量的数据点（MinPts），则该点被认为是核心对象。

         直接密度可达（Directly Density Reachable）：如果一个数据点在另一个数据点的邻域内，且另一个数据点是核心对象，则该数据点通过核心对象直接密度可达。

        基于以上概念，DBSCAN算法将数据点分为三种类型：

        核心对象：在其邻域内至少包含 MinPts 个数据点的数据点。

        边界点：不是核心对象，但位于核心对象的邻域内。

        噪声点（Noise Point）：既不是核心对象，也不是边界点。

        步骤分析：

        参数设置：设定两个参数，eps 表示邻域的半径，MinPts 表示一个核心对象所需的最少数据点个数。

        核心对象识别：对数据集中的每个数据点进行遍历，计算其邻域内的数据点数目，标记核心对象。（核心对象满足在其邻域内至少包含 MinPts 个数据点）

        聚类扩展：从任意未访问的核心对象开始，探索其直接密度可达的数据点进行连接并形成一个聚类。若边界点位于多个核心对象的邻域内，则将其分配给其中一个核心对象的聚类

        噪声点处理：将未分配到任何聚类的噪声点处理为离群点。

        算法特点：

        自动确定聚类数目：无需事先指定聚类数目，只需设定邻域半径 eps 和最小数据点数 MinPts。

        适用于任意形状的簇：DBSCAN能够有效地捕捉数据中的任意形状的聚类。

        对噪声数据鲁棒：能够将孤立点或噪声数据识别为离群点，不会干扰聚类过程。

        高效性：相对于K均值等算法，DBSCAN在处理大规模数据集时更为高效。

下面给出具体代码分析应用过程：这段代码演示了如何使用DBSCAN算法对生成的样本数据进行聚类，并对聚类结果进行评估和可视化。

首先，使用 make_blobs 生成了三个簇的样本数据，并进行了标准化处理。
然后，通过 DBSCAN 对标准化后的数据进行聚类，设置了 eps=0.3 和 min_samples=10 作为参数。
计算了聚类结果中的核心样本点，并对每个样本点进行了标记。
使用不同的评估指标（如均匀性、完整性、V-measure 等）评估了聚类结果的质量。
最后，通过可视化展示了聚类结果。将核心点和边界点以不同的大小和颜色进行绘制，用黑色表示噪声点。

import numpy as npfrom sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler# #############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,random_state=0)X = StandardScaler().fit_transform(X)# #############################################################################
# Compute DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)print('Estimated number of clusters: %d' % n_clusters_)
print('Estimated number of noise points: %d' % n_noise_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"% metrics.silhouette_score(X, labels))# #############################################################################
# Plot result
import matplotlib.pyplot as plt# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):if k == -1:# Black used for noise.col = [0, 0, 0, 1]class_member_mask = (labels == k)xy = X[class_member_mask & core_samples_mask]plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=14)xy = X[class_member_mask & ~core_samples_mask]plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=6)plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.savefig("../5.png", dpi=500)

实例运行结果如下图所示：

图中不同颜色的点表示不同的聚类簇，同一簇内的点颜色相同。
大点表示核心样本点，小点表示边界点。
黑色的点表示噪声点，即未分配到任何簇的样本点。
图像中心的聚类簇密集程度较高，周围的样本点则较为分散，符合DBSCAN对于密度聚类的特点。
通过图像可以直观地观察到聚类结果，评估聚类算法的性能和有效性。

02- 基于K均值的颜色量化实战

         基于K均值的颜色量化是一种常用的图像处理技术，可以将一幅彩色图像中的颜色数量减少，从而减小图像的尺寸，降低存储和处理的复杂度。下面是对基于K均值的颜色量化的详细分析：

        原理分析：

数据准备：将彩色图像中的每个像素看作是一个三维向量，表示红、绿、蓝（RGB）分量的取值。数据准备阶段即将图像中的所有像素点按照RGB值组织成一个数据集。
K均值算法：将数据集中的像素点以RGB向量的形式聚类成K个簇，使得每个像素点被分配到与之最近的簇中心，从而实现颜色压缩。
迭代优化：迭代地更新簇中心，直至达到收敛条件（如中心点不再变化、迭代次数达到上限等）。
颜色替换：将每个簇的颜色替换为该簇内所有像素点的平均颜色值。

        实现步骤：

初始化：随机选择K个像素点作为初始的簇中心。
簇分配：计算每个像素点与各个簇中心的距离，将其分配到最近的簇中心。
更新中心：更新每个簇中心为该簇内所有像素点的平均值。
迭代：重复步骤2和3直至满足终止条件。
颜色替代：将每个像素点的颜色替换为其所属簇的簇中心颜色。

        算法特点：

简单高效：K均值算法实现简单，易于理解和实现。
需预先确定K值：K均值算法需要事先确定聚类的数量K，不同的K值可能导致不同的聚类结果。
对初始化敏感：簇中心的初始化对最终结果有较大影响，可能会陷入局部最优解。
适用性广泛：K均值算法在颜色量化等应用领域效果较好，但对于异性方差较大的数据不太适用。

        应用领域：

图像压缩：通过减少颜色数量，可以降低图像的尺寸和存储空间。
图像处理：在图像编辑中，颜色量化可以用于图像风格迁移、图像复原等领域。
数据可视化：颜色量化也常用于将图像的颜色数目减少用于数据可视化等领域。

下面给出具体代码分析应用过程：这段代码实现了基于K均值的颜色量化，并使用了scikit-learn库中的KMeans模型进行颜色压缩。以下是对代码的简要解释和对生成的图像的详细分析：

加载中国宫殿的图像，并将图像转换为浮点数表示，范围在[0,1]之间。
将图像转换为2D的numpy数组，以便用于K均值算法。
随机选择1000个像素点的子样本用于训练K均值模型，并拟合模型。
使用训练好的K均值模型对整个图像进行颜色压缩，并预测各像素点的颜色类别。
使用随机选择的颜色作为参考，对整个图像进行颜色压缩并预测颜色类别。
定义recreate_image()函数以重新构建压缩后的图像。
显示原始图像、K均值颜色压缩后的图像和随机颜色压缩后的图像。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin
from sklearn.datasets import load_sample_image
from sklearn.utils import shuffle
from time import timen_colors = 64# Load the Summer Palace photo
china = load_sample_image("china.jpg")# Convert to floats instead of the default 8 bits integer coding. Dividing by
# 255 is important so that plt.imshow behaves works well on float data (need to
# be in the range [0-1])
china = np.array(china, dtype=np.float64) / 255# Load Image and transform to a 2D numpy array.
w, h, d = original_shape = tuple(china.shape)
assert d == 3
image_array = np.reshape(china, (w * h, d))print("Fitting model on a small sub-sample of the data")
t0 = time()
image_array_sample = shuffle(image_array, random_state=0)[:1000]
kmeans = KMeans(n_clusters=n_colors, random_state=0).fit(image_array_sample)
print("done in %0.3fs." % (time() - t0))# Get labels for all points
print("Predicting color indices on the full image (k-means)")
t0 = time()
labels = kmeans.predict(image_array)
print("done in %0.3fs." % (time() - t0))codebook_random = shuffle(image_array, random_state=0)[:n_colors]
print("Predicting color indices on the full image (random)")
t0 = time()
labels_random = pairwise_distances_argmin(codebook_random,image_array,axis=0)
print("done in %0.3fs." % (time() - t0))def recreate_image(codebook, labels, w, h):"""Recreate the (compressed) image from the code book & labels"""d = codebook.shape[1]image = np.zeros((w, h, d))label_idx = 0for i in range(w):for j in range(h):image[i][j] = codebook[labels[label_idx]]label_idx += 1return image# Display all results, alongside original image
plt.figure(1)
plt.clf()
plt.axis('off')
plt.title('Original image (96,615 colors)')
plt.imshow(china)
plt.savefig("../3.png", dpi=500)
plt.figure(2)
plt.clf()
plt.axis('off')
plt.title('Quantized image (64 colors, K-Means)')
plt.imshow(recreate_image(kmeans.cluster_centers_, labels, w, h))
plt.savefig("../4.png", dpi=500)
plt.figure(3)
plt.clf()
plt.axis('off')
plt.title('Quantized image (64 colors, Random)')
plt.imshow(recreate_image(codebook_random, labels_random, w, h))
plt.savefig("../5.png", dpi=500)
plt.show()

实例运行结果如下图所示：

原始图像（96,615种颜色）：展示了原始彩色图像，颜色细节丰富。
K均值颜色压缩后的图像（64种颜色）：经过K均值算法压缩处理，仅采用64种颜色表达图像，颜色数量减少，但整体色调保持。
随机颜色压缩后的图像（64种颜色）：使用随机选取的颜色进行压缩后的图像，色调会略有不同于K均值方法，但也达到了颜色量化的目的。

03- 分层聚类：结构化区域与非结构化区域

分层聚类是一种聚类分析方法，它通过逐步合并或分裂聚类来构建聚类层次结构。在图像处理领域中，分层聚类可以针对图像中的结构化区域（如边缘、纹理等）和非结构化区域（如背景、平坦区域等）进行分析和处理。下面是对分层聚类在处理结构化区域与非结构化区域的详细分析：

结构化区域和非结构化区域的特点：

结构化区域：通常指图像中具有明显纹理、边缘、形状等特征的区域，这些区域具有一定的规律性和重复性。
非结构化区域：指图像中较为平坦、连续的区域，缺乏明显的纹理和边缘特征，整体呈现较为均匀的颜色分布。

分层聚类在处理结构化区域和非结构化区域的应用：

结构化区域：

特征提取：分层聚类可以帮助提取结构化区域的特征，如边缘检测、纹理分析等，从而实现对结构化区域的定位和描述。
分割和识别：通过分层聚类，可以将图像中相似的结构化区域划分到同一聚类中，并进一步实现目标分割和识别。

非结构化区域：

背景提取：分层聚类可以帮助识别并提取出图像中的非结构化背景区域，实现对图像中主体与背景的分离。
颜色量化：将非结构化区域进行聚类处理，可以实现对颜色的量化和压缩，减少图像中的细节和噪声。

实现方法：

分层聚类算法选择：常用的分层聚类算法包括层次聚类、BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies）等，根据应用场景选择适合的算法。
特征提取与表示：针对结构化区域和非结构化区域提取合适的特征向量，可以是颜色、纹理、边缘等特征。
聚类处理：根据提取的特征向量进行分层聚类，构建聚类层次结构，将相似的区域合并或分裂。
结果分析和后处理：对于结构化区域，可以进一步处理提取的特征信息，对于非结构化区域，可以根据聚类结果进行后续处理，如背景提取、颜色量化等操作。

应用场景：

医学图像分析：对医学图像中的病变结构和正常组织进行区分和分析。
地图图像处理：识别地图中的道路、水域等结构化区域以及其他地物。
图像分割：将图像分割为不同的结构和区域，便于进一步处理和分析。

通过分层聚类对结构化区域和非结构化区域进行分析和区分，有助于更好地理解图像内容、实现图像分割和特征提取，并在各种图像处理应用中发挥作用。

下面给出具体代码分析应用过程：这段代码主要是使用了 scikit-learn 库进行分层聚类（Hierarchical Clustering）的示例代码，针对生成的瑞士卷数据集（Swiss Roll Dataset）进行了无连接约束和有连接约束两种情况的聚类分析，并将结果通过 3D 散点图可视化展示。下面对代码和生成的图像进行详细分析：

首先，使用 make_swiss_roll 生成含有噪音的瑞士卷数据集 X，然后将其变窄处理。
接着，使用 AgglomerativeClustering 进行分层聚类。首先对无连接约束的情况进行聚类（ward 连接方式，将数据分为 6 类），计算耗时并输出结果。
接着，根据数据结构构建连接度矩阵（这里使用的是最近的 10 个邻居），再次使用 AgglomerativeClustering 进行有连接约束的聚类，同样分为 6 类，计算耗时并输出结果。
最后，根据聚类结果绘制两幅3D散点图，分别展示了无连接约束和有连接约束下的聚类效果，并在标题中显示了计算耗时。

import time as time
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as p3
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_swiss_roll# #############################################################################
# Generate data (swiss roll dataset)
n_samples = 1500
noise = 0.05
X, _ = make_swiss_roll(n_samples, noise=noise)
# Make it thinner
X[:, 1] *= .5# #############################################################################
# Compute clustering
print("Compute unstructured hierarchical clustering...")
st = time.time()
ward = AgglomerativeClustering(n_clusters=6, linkage='ward').fit(X)
elapsed_time = time.time() - st
label = ward.labels_
print("Elapsed time: %.2fs" % elapsed_time)
print("Number of points: %i" % label.size)# #############################################################################
# Plot result
fig = plt.figure()
ax = p3.Axes3D(fig)
ax.view_init(7, -80)
for l in np.unique(label):ax.scatter(X[label == l, 0], X[label == l, 1], X[label == l, 2],color=plt.cm.jet(np.float(l) / np.max(label + 1)),s=20, edgecolor='k')
plt.title('Without connectivity constraints (time %.2fs)' % elapsed_time)
plt.savefig("../4.png", dpi=500)# #############################################################################
# Define the structure A of the data. Here a 10 nearest neighbors
from sklearn.neighbors import kneighbors_graph
connectivity = kneighbors_graph(X, n_neighbors=10, include_self=False)# #############################################################################
# Compute clustering
print("Compute structured hierarchical clustering...")
st = time.time()
ward = AgglomerativeClustering(n_clusters=6, connectivity=connectivity,linkage='ward').fit(X)
elapsed_time = time.time() - st
label = ward.labels_
print("Elapsed time: %.2fs" % elapsed_time)
print("Number of points: %i" % label.size)# #############################################################################
# Plot result
fig = plt.figure()
ax = p3.Axes3D(fig)
ax.view_init(7, -80)
for l in np.unique(label):ax.scatter(X[label == l, 0], X[label == l, 1], X[label == l, 2],color=plt.cm.jet(float(l) / np.max(label + 1)),s=20, edgecolor='k')
plt.title('With connectivity constraints (time %.2fs)' % elapsed_time)
plt.savefig("../5.png", dpi=500)
plt.show()

实例运行结果如下图所示：

无连接约束聚类结果：图像中展示了数据点按照聚类结果着色，并在三维空间中展示其分布情况。不同颜色代表不同的聚类簇，展示了数据点的聚类效果。
有连接约束聚类结果：同样是根据聚类结果着色展示数据点的分布情况，不同颜色代表不同的聚类簇。由于考虑了数据点之间的连接性，聚类效果可能会有所不同。

04- 不同度量的聚集聚类实战

在数据挖掘和机器学习领域中，聚集聚类（Agglomerative Clustering）是一种常见的聚类算法，它通过不断地将最相近的数据点或簇进行合并来构建聚类结构。在聚集聚类中，存在多种不同的度量方法用于衡量数据点之间的相似性或距离，从而影响最终的聚类结果。以下是一些常用的度量方法：

欧氏距离（Euclidean Distance）：最常见的距离度量方法之一，计算两个数据点之间的直线距离。欧氏距离适用于数据特征为连续值的情况。

曼哈顿距离（Manhattan Distance）：也称为城市街区距离，计算两个数据点在各个坐标轴上的距离总和。适用于特征为连续值的情况。

切比雪夫距离（Chebyshev Distance）：计算两个数据点在各个坐标轴上的最大差值。适用于处理数据缩放不一致的情况。

闵可夫斯基距离（Minkowski Distance）：欧氏距离和曼哈顿距离的泛化形式，可以通过参数来控制距离的计算方式。

余弦相似度（Cosine Similarity）：用于衡量两个向量之间的夹角余弦值，而非距离，适用于处理文本数据或稀疏数据。

选择合适的距离度量方法对聚集聚类的结果影响巨大，不同的数据特点和应用场景可能需要不同的度量方法来获得最佳的聚类效果。在实际应用中，可以根据数据的特征和领域知识来选择合适的距离度量方法，以及调整算法参数来优化聚类结果。

下面给出具体代码分析应用过程：这段代码主要是对生成的波形数据进行聚类分析，并使用不同的距离度量（余弦距离、欧氏距离、曼哈顿距离）来比较聚类结果。代码中的主要步骤包括：

生成具有三种波形模式的数据集，每种模式有30个样本。
绘制基本波形数据的真实标签情况，展示每种波形模式的数据分布情况。
计算不同波形类别之间的平均距离，并绘制热图展示不同度量方式下的类间距离情况。
使用层次聚类算法（Agglomerative Clustering）对数据进行聚类，分别使用余弦距离、欧氏距离、曼哈顿距离进行聚类，并绘制聚类结果图像。

import matplotlib.pyplot as plt
import numpy as npfrom sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distancesnp.random.seed(0)# Generate waveform data
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)def sqr(x):return np.sign(np.cos(x))X = list()
y = list()
for i, (phi, a) in enumerate([(.5, .15), (.5, .6), (.3, .2)]):for _ in range(30):phase_noise = .01 * np.random.normal()amplitude_noise = .04 * np.random.normal()additional_noise = 1 - 2 * np.random.rand(n_features)# Make the noise sparseadditional_noise[np.abs(additional_noise) < .997] = 0X.append(12 * ((a + amplitude_noise)* (sqr(6 * (t + phi + phase_noise)))+ additional_noise))y.append(i)X = np.array(X)
y = np.array(y)n_clusters = 3labels = ('Waveform 1', 'Waveform 2', 'Waveform 3')# Plot the ground-truth labelling
plt.figure()
plt.axes([0, 0, 1, 1])
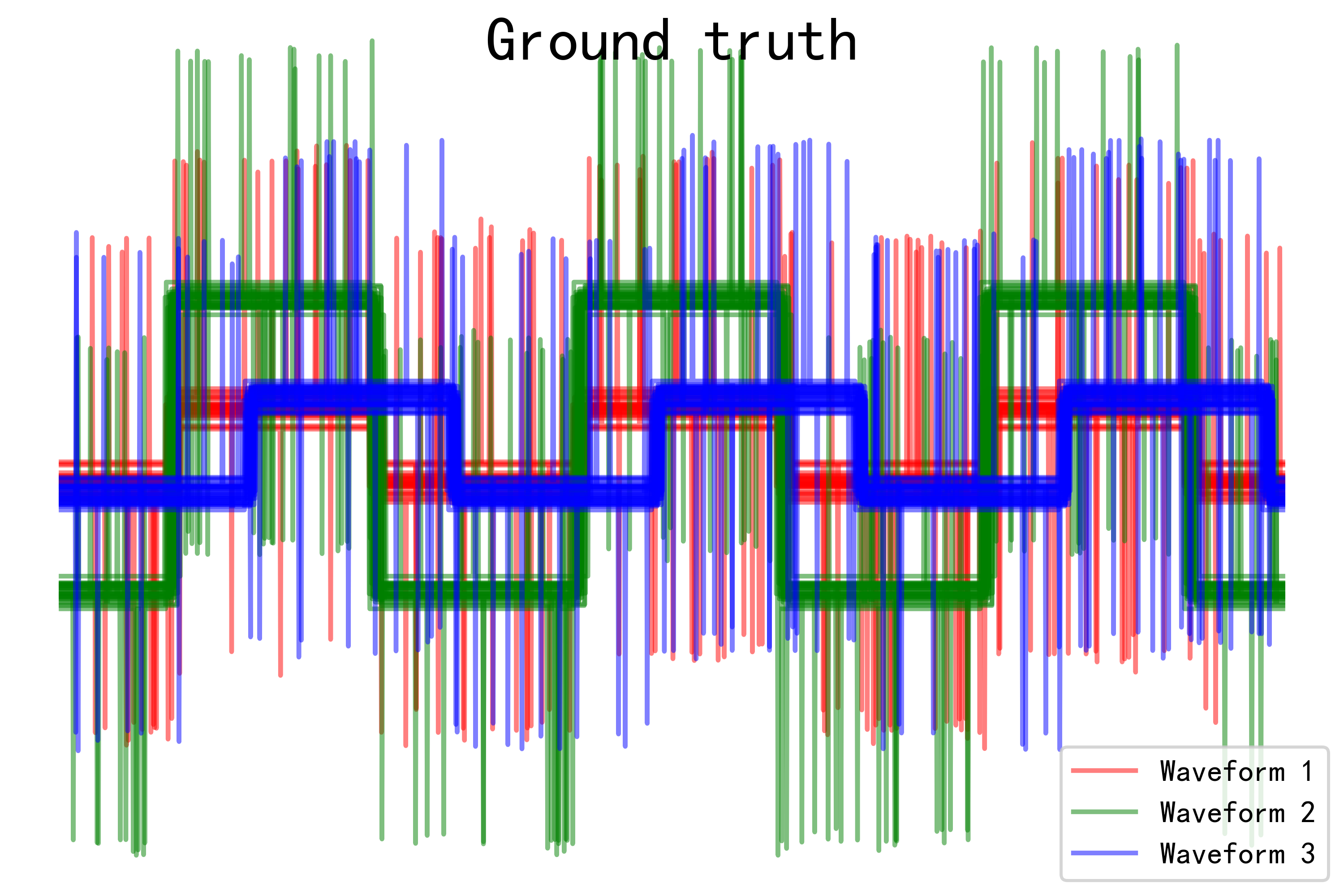
for l, c, n in zip(range(n_clusters), 'rgb',labels):lines = plt.plot(X[y == l].T, c=c, alpha=.5)lines[0].set_label(n)plt.legend(loc='best')plt.axis('tight')
plt.axis('off')
plt.suptitle("Ground truth", size=20)
plt.savefig("../5.png", dpi=500)# Plot the distances
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):avg_dist = np.zeros((n_clusters, n_clusters))plt.figure(figsize=(5, 4.5))for i in range(n_clusters):for j in range(n_clusters):avg_dist[i, j] = pairwise_distances(X[y == i], X[y == j],metric=metric).mean()avg_dist /= avg_dist.max()for i in range(n_clusters):for j in range(n_clusters):plt.text(i, j, '%5.3f' % avg_dist[i, j],verticalalignment='center',horizontalalignment='center')plt.imshow(avg_dist, interpolation='nearest', cmap=plt.cm.gnuplot2,vmin=0)plt.xticks(range(n_clusters), labels, rotation=45)plt.yticks(range(n_clusters), labels)plt.colorbar()plt.suptitle("Interclass %s distances" % metric, size=18)plt.tight_layout()
plt.savefig("../4.png", dpi=500)# Plot clustering results
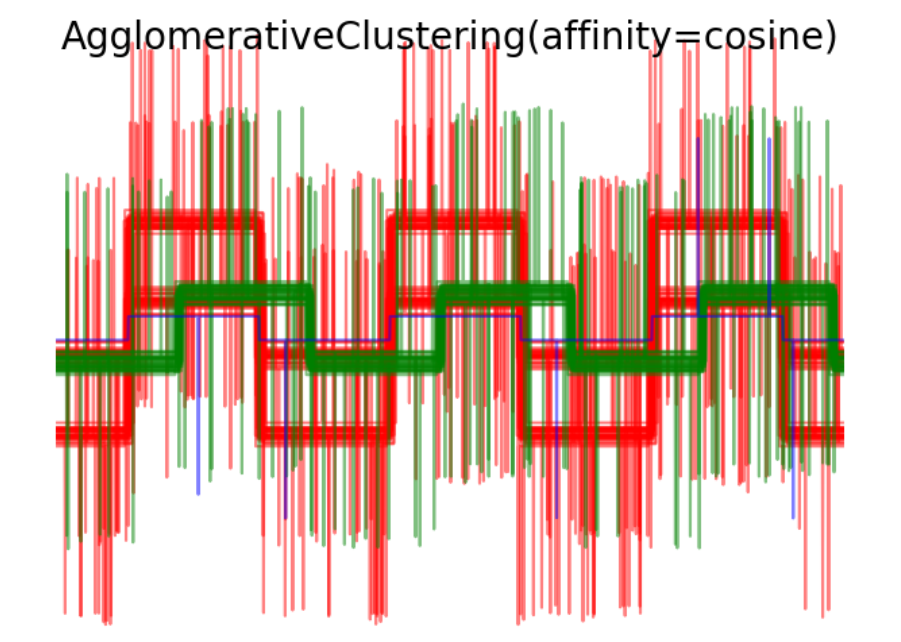
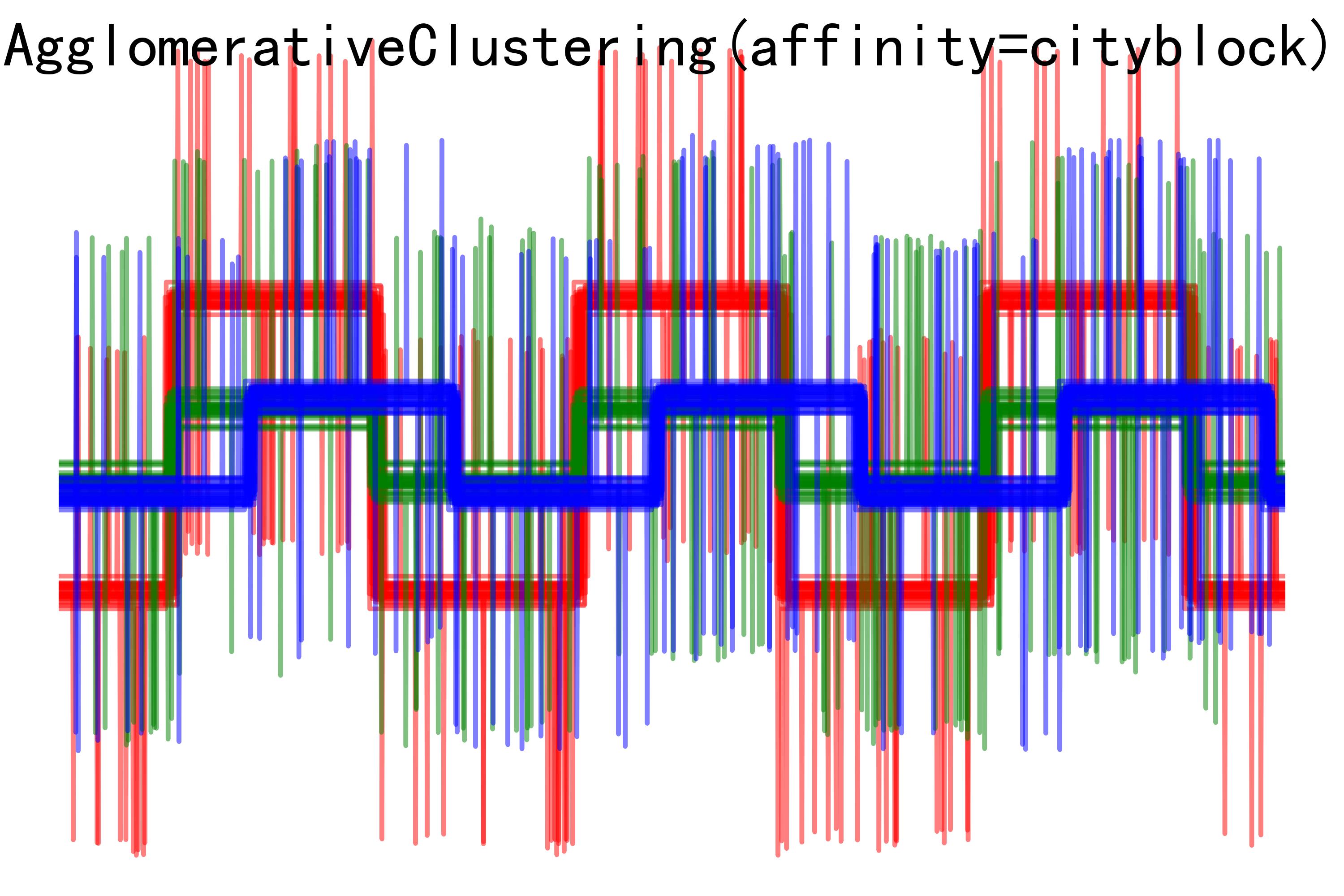
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):model = AgglomerativeClustering(n_clusters=n_clusters,linkage="average", affinity=metric)model.fit(X)plt.figure()plt.axes([0, 0, 1, 1])for l, c in zip(np.arange(model.n_clusters), 'rgbk'):plt.plot(X[model.labels_ == l].T, c=c, alpha=.5)plt.axis('tight')plt.axis('off')plt.suptitle("AgglomerativeClustering(affinity=%s)" % metric, size=20)plt.savefig("../3.png", dpi=500)
plt.show()

实例运行结果如下图所示：

Ground truth图像：展示了真实标签下每种波形模式的数据分布情况，可以清晰地看到不同波形之间的差异。
Interclass distances热图：展示了不同波形类别之间的平均距离，浅色表示距离较远，深色表示距离较近，有助于比较不同距离度量方式下的类间相似性。
AgglomerativeClustering聚类结果图像：展示了使用不同距禈度量方式进行聚类后的结果。每种波形模式使用不同颜色表示，可以观察到不同聚类方法下对数据的聚类效果。

总结

在机器学习领域，常用的聚类算法包括DBSCAN聚类算法、K均值聚类算法、以及分层聚类算法。这些算法在处理不同类型的数据和应用场景中都有各自的优势和适用性。

DBSCAN聚类算法（Density-Based Spatial Clustering of Applications with Noise）：

优点：能够发现任意形状的聚类，对噪声数据比较鲁棒。
工作原理：通过定义邻域内的数据点密度来确定聚类，从而将高密度区域划分为一个聚类，并能够有效处理密度不均匀的数据集。

K均值聚类算法（K-Means Clustering）：

优点：简单且高效，适用于大规模数据集。
工作原理：将数据点划分为K个簇，通过不断迭代更新簇的中心点和重新分配数据点来最小化簇内的方差。

分层聚类算法（Hierarchical Clustering）：

优点：能够构建聚类簇之间的层次结构，不需要预先指定簇的数量。
工作原理：通过不断合并或分裂数据点或簇来构建聚类层次结构，可分为凝聚性层次聚类和分裂性层次聚类两种方法。

不同度量的聚集：

聚集聚类是一种基于簇的层次聚类算法，采用不同的距离或相似度度量方法来决定簇之间的合并顺序。
不同度量方法会影响聚类的结果，常用的度量包括欧氏距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离和余弦相似度等。

总的来说，选择适合数据特点和需求的聚类算法和距离度量方法是十分重要的。DBSCAN适用于发现任意形状的聚类，K均值适用于均衡分布的数据，分层聚类适用于构建聚类层次结构。同时，根据数据的特点和任务需求选择合适的距离度量方法也是关键的一步。