聚集专题

可以进行非机动车违停、人员聚集、临街摆摊、垃圾满溢、烟雾火情等城市治理场景的智能识别的智慧城管开源了

智慧城管视觉监控平台是一款功能强大且简单易用的实时算法视频监控系统。它的愿景是最底层打通各大芯片厂商相互间的壁垒，省去繁琐重复的适配流程，实现芯片、算法、应用的全流程组合，从而大大减少企业级应用约95%的开发成本。基于深度学习技术及强大的专家团队，针对多个工业垂类场景进行算法优化，打造最优的工业AI算法模型，提供更加精准的工业AI模型库，客户可直接选择适合自己业务场景的模型，快速实现业务落地

谈谈分组：sql的group by+聚集函数和 python的groupby+agg

直接举例子+分析例子+总结来说，我先给几个表：学生表：student(学号，姓名，年龄，院系)；课程表：course(课程号，课程名，学分)；学生选课表：sc(学号，课程号，分数)；啥时候用分组呢？我由简至深来谈。 1、比如让我们查询各个课程号及相应的选课人数。首先定位到sc表上，“各个”很明显就是要按课程分组，group by出场了，分组后对每组去统计选课人数，聚集函数出场了。

SQL 中聚集索引

今天做个试验，验证下聚集索引是不是改变表的物理结构。第一步：创建表 --只有聚集索引CREATE TABLE Department(DepartmentID int IDENTITY(1,1) NOT NULL PRIMARY KEY,Name NVARCHAR(200) NOT NULL,GroupName NVARCHAR(200) NOT NULL,Company NVARCHAR(

【线性相关 vs 双变量回归】数据点在斜率周围的聚集程度与斜率本身并不是一回事。

相关性分析（具体来说，皮尔逊成对相关性）和回归分析（具体来说，双变量最小二乘 (OLS) 回归）具有许多共同的特征：两者都定期应用于两个连续变量（我们称之为 X 和 Y）。通常向学生介绍这两种图表时使用的是同一类型的图表：散点图。二者从根本上讲都是关于 X 中的偏差（即相对于平均值的单个值）与 Y 中的偏差之间的关系。两者都假设 X 和 Y 之间存在线性关系。两者都可以用于经典的假设检验，每个

12【MySQL必知必会】汇总数据（聚集函数）

SQL语句 /*第12章汇总数据关键词：聚集函数（aggregate function）*//* SQL聚集函数AVG():返回某列的平均值COUNT():返回某列中的行数MAX():返回某列中的最大值MIN():返回某列中的最小值SUM():返回某列中的和*/-- 计算产品表中所有产品的平均价格SELECT AVG(prod_price) AS avg_priceFROM

Hadoop YARN配置参数剖析(2)—权限与日志聚集相关参数

本文转自 http://dongxicheng.org/mapreduce-nextgen/hadoop-yarn-configurations-log-aggregation/ 注意，配置这些参数前，应充分理解这几个参数的含义，以防止误配给集群带来的隐患。另外，这些参数均需要在yarn-site.xml中配置。 1. 权限相关配置参数这里的权限由三部分组成，分别是：（1）

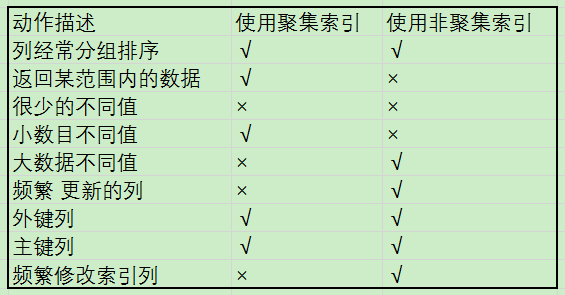
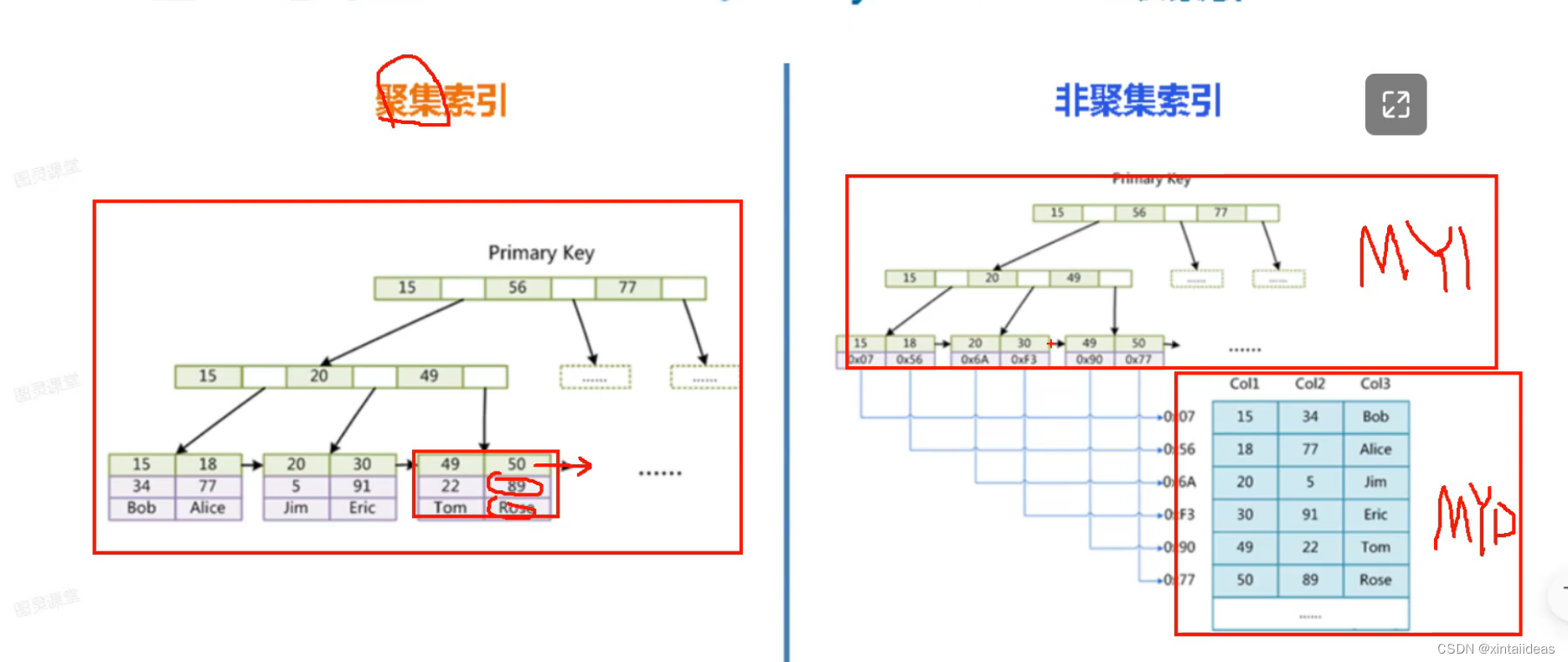
快速理解聚集索引和非聚集索引

数据库的索引，听起来挺神秘的，仔细想想。这些索引，其实就是平时咱们查东西时候常用的两种手段。无非就是为了提高我们找东西的效率而已。那么我们平时又是怎么查东西呢？聚集索引：聚集索引，来源于生活尝试。这中索引可以说是按照数据的物理存储进行划分的。对于一堆记录来说，使用聚集索引就是对这堆记录进行堆划分。即主要描述的是物理上的存储。举个例子：

mysql 获取今年至今的按照周聚集的统计

主要就是使用week 函数聚集数据 SELECT DATE_ADD(CONCAT(SUBSTRING(`time`,1,4),'-1-1') ,INTERVAL WEEK(`time`) WEEK) `startofweek`,SUM(income_total) FROM statistic WHERE `time` >= CONCAT(SUBSTRING(CU

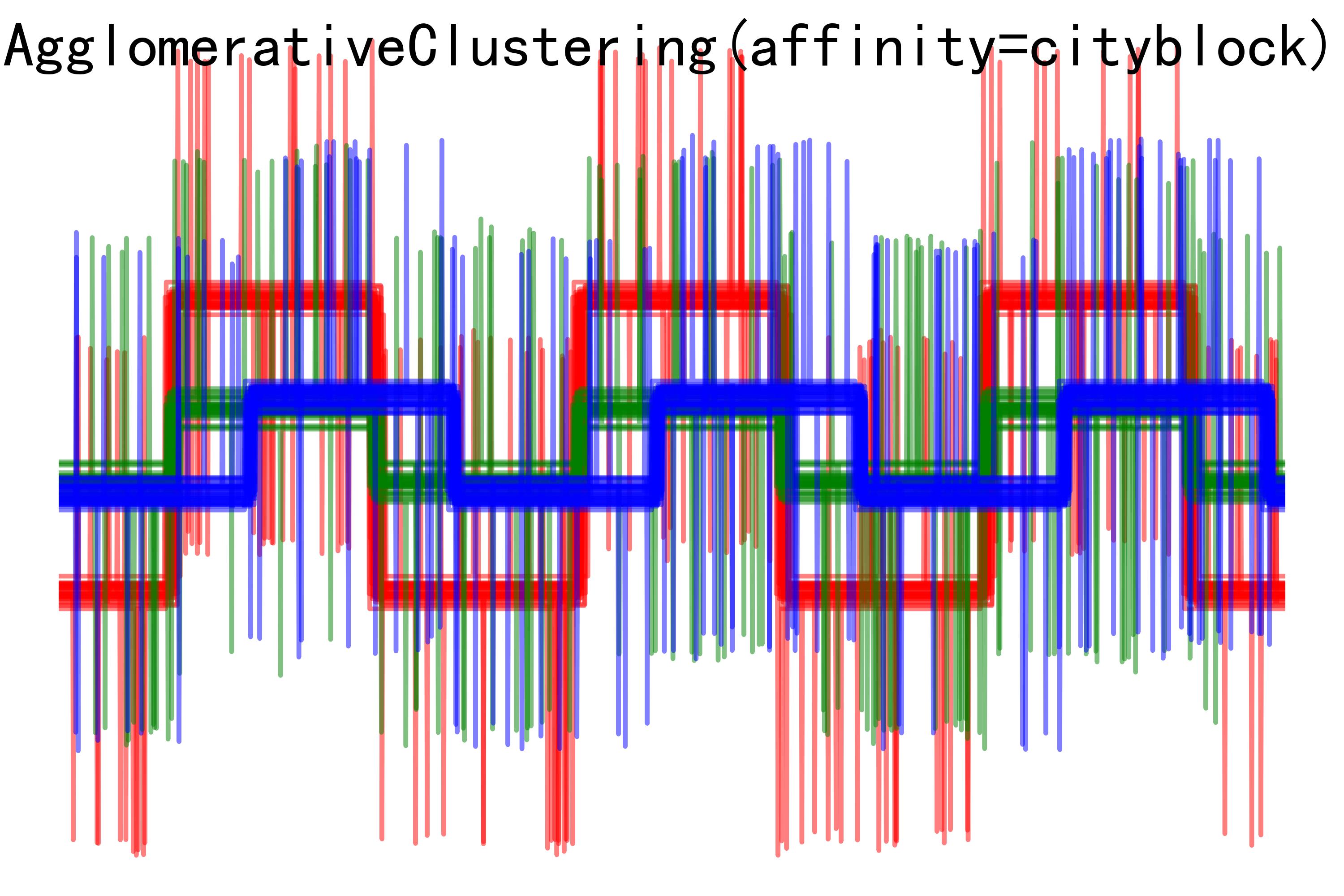
【机器学习聚类算法实战-5】机器学习聚类算法之DBSCAN聚类、K均值聚类算法、分层聚类和不同度量的聚集聚类实例分析

🎩 欢迎来到技术探索的奇幻世界👨‍💻 📜 个人主页：@一伦明悦-CSDN博客 ✍🏻 作者简介： C++软件开发、Python机器学习爱好者 🗣️ 互动与支持：💬评论 👍🏻点赞 📂收藏 👀关注+ 如果文章有所帮助，欢迎留下您宝贵的评论，点赞加收藏支持我，点击关注，一起进步！目录前言正文 01- DBSCAN聚类算法简

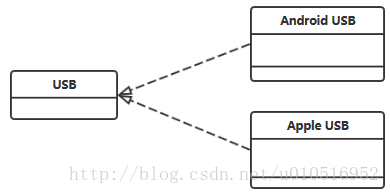
类图中的依赖、关联、聚集、构成、泛化、实现关系

一、依赖(Dependency) 依赖：A类依赖B类，在B类发生变化时，A类也会随着B类发生变化；通常依赖的类是作为参数传入。 1. Car类是User类中的（某个方法的）局部变量； 2. Car类是User类方法当中的一个参数； 3. Car类向User类发送消息，从而影响B类发生变化；二、关联(Association) 关联：表示订单与产品对象之间存在关系；关联关

华为OD机试【城市聚集度】(java)(200分)

1、题目描述一张地图上有N个城市，城市和城市之间有且只有一条道路相连，要么直接相连，要么通过其他城市中转相连(可中转一次或多次)。城市与城市之间的道路都不会成环。当切断通往某城市i的所有道路后，地图上将分成多个连通的城市群，设该城市i的聚集度为DPi of Polymerization), DPi = max(城市群1的城市个数，城市群2的城市个数，…城市群m的城市个数)。请找出地图上DP

【IP：Internet Protocol,子网（Subnets）,IPv6：动机,层次编址：路由聚集（rout aggregation）】

文章目录 IP：Internet Protocol互联网的的网络层IP分片和重组（Fragmentation & Reassembly）IP编址：引论子网（Subnets）特殊IP地址IP 编址: CIDR子网掩码（Subnet mask）转发表和转发算法如何获取一个IP地址？DHCP: Dynamic Host Configuration ProtocolDHCP: 不仅仅是IP addr

达梦(DM) SQL聚集函数及日期运算操作

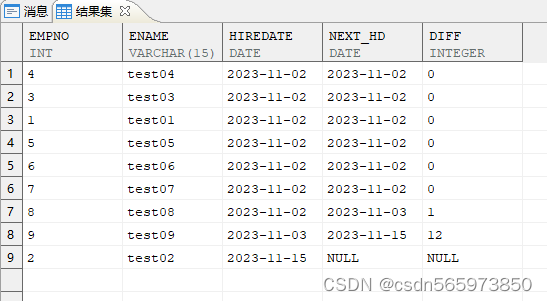
达梦DM SQL聚集函数及日期运算操作聚集函数MAX、MIN、SUM、AVG、COUNT使用分析函数 sum (…) over (order by…) 可以生成累计和更改累计和的值计算出现次数最多的值日期运算加减日、月、年加减时、分、秒日期间隔之时、分、秒日期间隔之日、月、年求两个日期间的工作天数确定当前记录和下一条记录之间相差的天数这里讲解DM数据库的操作，主要涉及聚集函

聚集索引实例

参考文章：数据库索引实例在Sql Server2000中创建测试数据库，接着创建数据库表并插入数据，sql代码如下： USE twt001IF EXISTS (SELECT * FROM INFORMATION_SCHEMA.TABLES WHERE TABLE_NAME = 'emp_pay')DROP TABLE emp_payGOUSE twt001IF EXISTS (S

聚集索引，非聚集索引，覆盖索引，

前段时间，公司一个新上线的网站出现页面响应速度缓慢的问题，一位负责这个项目的但并不是搞技术的妹子找到我，让我想办法提升网站的访问速度，因为已经有很多用户来投诉了。我第一反应觉的是数据库上的问题，假装思索了一下，摆着一副深沉炫酷的模样说：“是不是数据库查询上出问题了，给表加上索引吧”，然后妹子来了一句：“现在我们网站访问量太大，加索引有可能导致写入数据时性能下降，影响用户使用的”。当时我就楞了

【postgresql 基础入门】入门教程成形了，八大章节，涵盖库，表，事务，约束，数据类型，聚集函数，轻松入门

Postgresql 基础入门专栏内容： postgresql内核源码分析手写数据库toadb并发编程个人主页：我的主页管理社区：开源数据库座右铭：天行健，君子以自强不息；地势坤，君子以厚德载物. 序言 PostgreSQL，简称PG，是一款强大的开源关系型数据库管理系统, 近年来参与者越来越多，开源社区趋于成熟，因为它的开源和开放，很多其它数据库的从业者也转向

mysql必知必会--学习笔记（6）--日期操作Date,Time,聚集函数，AVG,MAX,MIN

1、mysql支持日期型的数据，而且日期的格式应采用xxxx-xx-xx的格式进行保存，而日期应选择 xx：xx：xx的格式进行保存。 2、如果某一列是DateTime型的数据，例如published_time 那么使用DATE（published_time）可以提取出日期部分，使用TIME（published_time)提取出时间的部分。用YEAR（published_time)提取出年

数据仓库——聚集

数据仓库基础笔记思维导图已经整理完毕，完整连接为：数据仓库基础知识笔记思维导图聚集在对性能不断探索的过程中，聚集是最强大最、有效的数据处理工具。通过仔细规划和集成，聚集将队数据仓库性能产生巨大影响。无需针对特定的软件和硬件进行大量的投资，使用在数据仓库中已经存在的工具即可。与导出模式类似，聚集是一种补充性的数据结构，用来加快工作进度。聚集主要是通过汇总数据来获得改进性能的效果。但是，

【文献分享】通过形态扫描仪阐明自组装肽聚集：蛋白质-肽结构表征的新工具

题目：Elucidating Self‐Assembling Peptide Aggregation via Morphoscanner: A New Tool for Protein‐Peptide Structural Characterization 通过形态扫描仪阐明自组装肽聚集：蛋白质-肽结构表征的新工具自组装和分子折叠在自然界中无处不在：它们驱动从生物到 DNA 分子等系统的组织。

MySQL 中聚集索引、非聚集索引、覆盖索引、索引下推到底是什么

一、什么是聚集索引、非聚集索引在MySQL数据库中，索引是提高查询效率的关键。而聚集索引、非聚集索引、覆盖索引、索引下推其实是索引优化的重要策略之一。那这些名词的含义到底是什么呢？在开始分析前，先来了解下 B+ 树的索引结构和回表查询： B+ 树结构 B+树是 B树的变体，将树的结构分为了叶子节点和非叶子节点。其中非叶子节点不存储具体数据，只存放主键和指向下一级数据的指针。而叶子

聚集在腾讯CSIG的T5科学家，究竟是怎样的存在？

“T5”在腾讯是怎么样的存在？这个问题，如果给两万名腾讯技术人员来回答，大部分的答案估计只有一个字 —— 神。要知道，在腾讯职级能力体系里，大多数人达到T3已殊为不易，已是人才市场上的重要参照。腾讯对T5科学家的评定标准极其严苛：他们不仅要是各自领域公认的资深专家，还需要有足够的战略眼光参与公司重大领域和项目。这让创立20年的腾讯T5科学家极为稀缺，此前他们像七龙珠一般星

次氯酸双光子聚集诱导发光型分子探针/聚集诱导发光环状多烯类分子/氮杂环聚集诱导发光分子的研究

瑞禧小编分享了次氯酸双光子聚集诱导发光型分子探针/聚集诱导发光环状多烯类分子/氮杂环聚集诱导发光分子的制备，一起来看！聚集诱导发光环状多烯类分子的制备：研究了4H-pyrans,fulvenes,siloles等环状多烯结构的小分子荧光染料在溶液,固态及薄层层析板上的荧光发射行为。与大多数传统的荧光染料小分子不同,这些多烯类荧光染料分子在稀溶液中基本没有荧光,而在聚集态下呈现非常明亮的

添加聚集索引后高效分页查询的效率

本人使用的是sql 2012数据库 ALTER proc [dbo].[ex2](@count int --次数)asbegindeclare @i intset @i = 0while @i < @countbeginSELECT * FROM product0 WHERE[bName] like '%23%'Order by grade desc,createTime

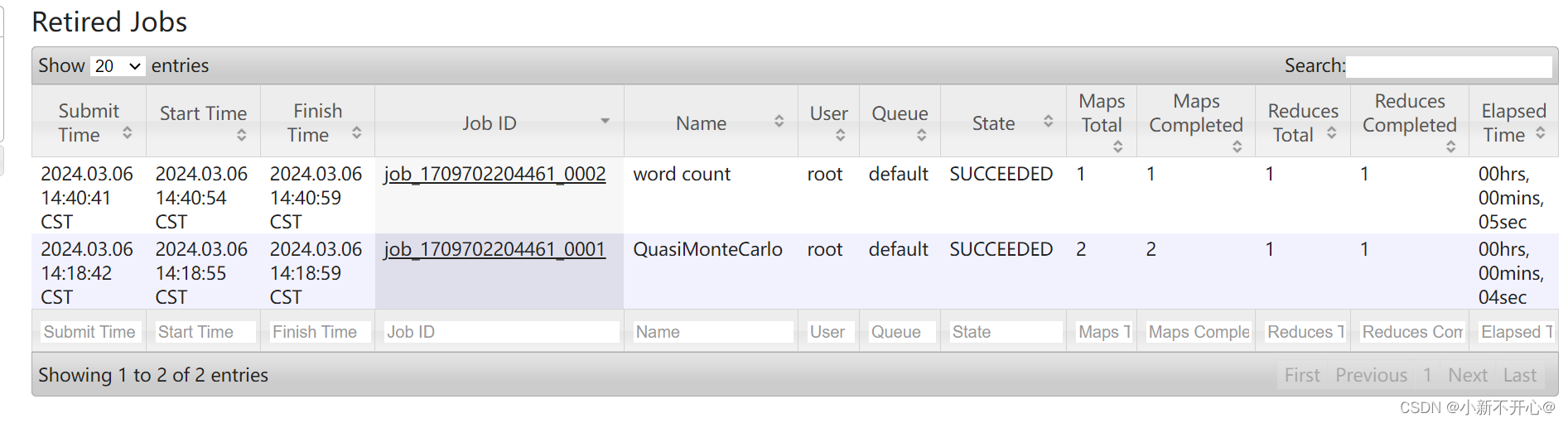
Hadoop配置日志的聚集——jobhistory不显示任务问题

问题：一开始job history是正常的，配置了日志的聚集以后不管做什么任务都不显示任务，hdfs是正常运行，而且根据配置步骤都重启过了。下面先po出日志聚集的操作步骤，再讲问题 1.配置yarn-site.xml cd $HADOOP_HOME/etc/hadoop vim yarn-site.xml 添加如下代码 <property><

什么是聚簇索引与非聚集索引和区别?

什么是聚簇索引与非聚集索引和区别? 按物理存储分类:InnoDB的存储方式是聚集索引，MVISAM的存储方式是非聚集索引 test innodb.frm 测试 innodb.ibd Frame=表结构数据表索引+数据 test myisam.frm ---->Frame=表结构test myisam.MYD_---数据=表数据test_myisam.MYl----MyISAM Index=表索引

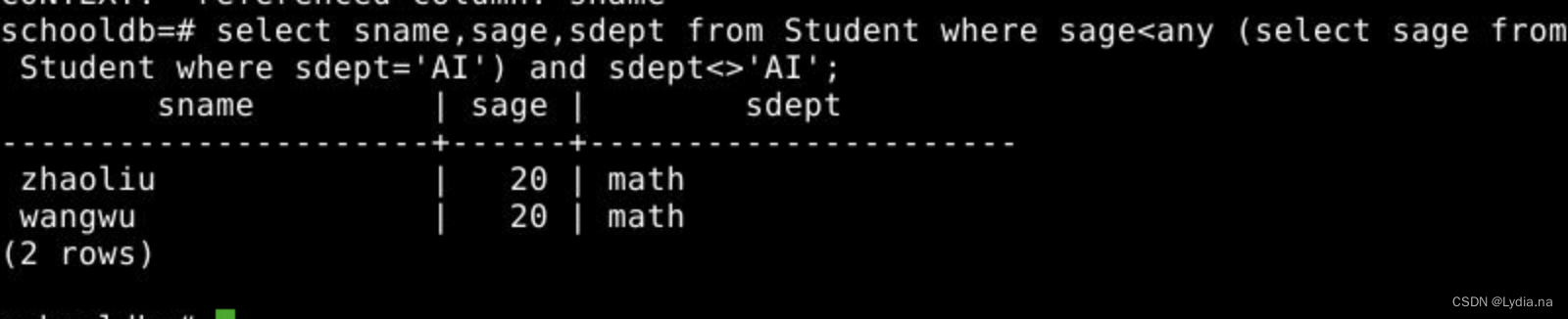
【数据库】实验五数据库综合查询｜多表查询、聚集函数、orderby、groupby

文章目录参考文章本文在实验四的基础上增加了orderby、聚集函数、groupby、多表查询的知识点，相较于上一次实验的难度变大了，嵌套表达更多了，逐渐开始套娃…… 其实可以看成一个偏正短语来拆分，再写成SQL语句，比如查询一个年龄大于20的学生成绩，那么学生成绩就为中心语，年龄大于20则作为修饰语，将中心语放至select ...from之间，依次类推进行分析。查询‘